全文共8000余字，预计阅读时间约16~27分钟 | 满满干货(附代码)，建议收藏！

代码下载点这里

一、介绍

CART（Classification and Regression Trees）即分类回归树，是一种重要的机器学习算法，既可以用于分类问题，也可以用于回归问题，因此在实际应用中具有很高的灵活性。然而，要理解并熟练使用CART树，需要掌握一些关键的概念和技巧。

CART树的理论部分文章请看这里：

机器学习(十六)：决策树

本文详细讲解如何在Sklearn中依次实现CART回归树和分类树，包括如何导入数据，预处理数据，建立模型，训练模型，进行预测，和评估模型。

二、CART分类树评估器参数详解

CART分类树是二叉树，其每个内部节点不是分为两个子节点，就是没有子节点（也就是叶节点）。这和其他可能有多于两个子节点的决策树算法（如ID3，C4.5等）有所不同。在CART分类树中，每个内部节点都对应一个输入特征和一个切分点，然后根据特征的值是否大于切分点将数据分配到左子节点或右子节点。每个叶节点对应一个预测类别，这个类别是其包含的训练样本中最常见的类别。

构建CART分类树的过程是一个递归的过程。

首先，算法会在所有可能的特征和所有可能的切分点中，选择出使得划分后的子集纯度最高（或者说不纯度降低最大）的特征和切分点。然后，算法会使用这个特征和切分点将数据划分为两个子集，分别对应左子节点和右子节点。接着，算法会分别在这两个子节点上重复这个过程，直到满足某个停止条件，比如树达到最大深度，或者一个节点中的样本数量少于某个阈值等。

DecisionTreeClassifier评估器参数众多，并且大多和决策树的模型结构相关，在Sklearn中还是通过这种方式来查看：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.tree import DecisionTreeClassifier

DecisionTreeClassifier?

看下结果：

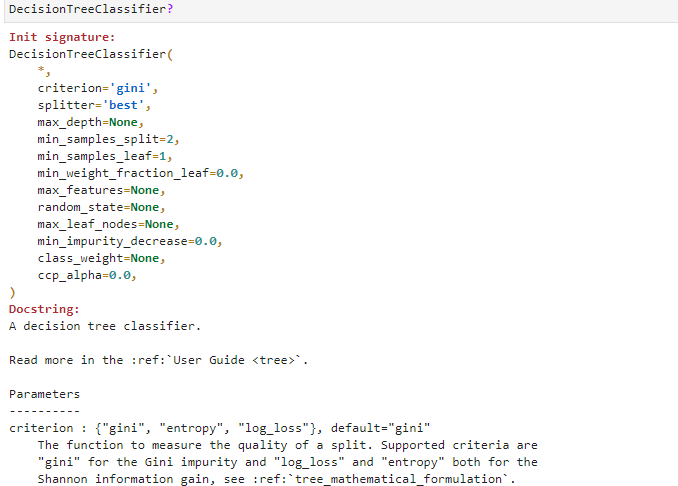
详细的看一下参数：

对于这些参数，可以将其分成三大类来理解。

2.1 模型评估类参数

• criterion：不纯度衡量指标

在sklearn中，树模型在默认情况下是CART树，CART树默认评估指标是“gini”，但也可以使用信息熵来衡量不纯度。

大多数情况下选择哪个指标并不会实质影响树模型的结构，但相比信息熵，基尼系数复杂度更低、计算速度更快，一般情况下推荐使用基尼系数。如果一定要寻找二者在使用上的不同，一般认为在有些情况下，基尼不纯度更倾向于在数据集中分割出多数类，而信息熵则更倾向于生成出更加平衡的树。

• ccp_alpha：结构风险权重

ccp是复杂度剪枝（Cost-Complexity Pruning）的简称，在sklearn的0.22版本中才被加入，是唯一一个为实现CART原生原理中的剪枝过程所设置的参数。

该参数并不是一个必选参数。带ccp项的剪枝也被称为最小复杂度剪枝，其原理是在决策树的损失函数上加上一个结构风险项，类似于正则化项在线性方程的损失函数中作用相同。

比如设T为某决策树，$R(T)$为决策树在训练集上整体不纯度，即代表模型的经验风险，令$\alpha |\tilde{T}|$表示模型结构风险，其中$\alpha$为参数，$|\tilde{T}|$为树的叶节点数量，则模型损失函数如下：
$$R_{\alpha }(T)=R(T)+\alpha |\tilde{T}|\text{\hspace{1em}(1)}$$
其中$R_{\alpha }(T)$就是加入风险结构项后的损失函数，而$\alpha$则是风险结构项的系数。由此可知，$\alpha$取值越大、对模型的结构风险惩罚力度就越大、模型结构就越简单、过拟合就能够被更好的抑制。

2.2 树结构控制类参数

关于控制树模型结构的相关参数，是最多的一类参数。

• max_depth、max_leaf_nodes：限制模型整体结构

• min_samples_split、min_samples_leaf：从节点样本数量角度限制树生长

• min_impurity_split和min_impurity_decrease：从降低损失值角度限制树生长的参数

通过这些参数的共同作用，从各角度有效限制树的生长。对于树模型来说，叶节点太多、单独叶节点所包含的样本数量太少、内部节点再划分降低的基尼系数较少，都是可能是过拟合的表现，在建模时尤其需要注意。

2.3 迭代随机过程控制类参数

• splitter

当该参数取值为random时是随机挑选分类规则对当前数据集进行划分

• max_features

该参数可以任意设置最多带入几个特征进行备选规律挖掘，只要该参数的设置不是带入全部特征进行建模，就相当于是给备选特征随机划个范围，也相当于是给树模型的训练增加了一定的随机性。

这两个参数可以提升模型训练速度，例如：如果只从个别特征中挑选最佳划分规则，或者随机生成一个划分规则、不进行比较就直接使用，能够极大节省计算量，只不过这也是一种用精度换效率的方式，如此操作肯定会带来模型结果精度的下降。

2.4 Sklearn 调用示例

直接上代码：

import numpy as np
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt

def train_and_plot_decision_tree(X, y):
    # 调用决策树评估器并进行训练
    clf = DecisionTreeClassifier().fit(X, y)
    
    # 输出模型在训练集上的评分
    score = clf.score(X, y)
    print(f'The accuracy score of the model on the training set: {score}')

    # 绘制决策树
    plt.figure(figsize=(6, 2), dpi=150)
    plot_tree(clf)
    plt.show()

# 使用方法
X = np.array([[1, 1], [2, 2], [2, 1], [1, 2], [1, 1], [1, 2], [1, 2], [2, 1]])
y = np.array([0, 0, 0, 1, 0, 1, 1, 0])

train_and_plot_decision_tree(X, y)

结果如下：

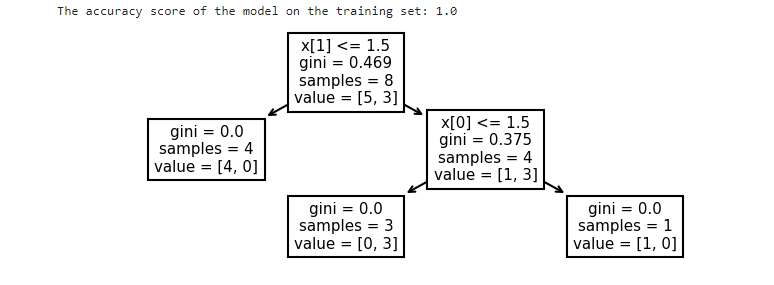
根据输出的结果可看出，sklearn中分类树的建模过程就是先根据第一个特征的不同取值进行数据集划分，然后在根据第二个特征的不同取值进行数据集划分，最终形成一个三个叶节点、两层的决策树模型。

三、CART回归树建模流程

3.1 CART回归树的基本建模流程

通过一个实验来模拟CART树的建模流程。

Step 1：假设有以下数据集，该数据集只包含一个特征和一个连续型标签：

data = np.array([[1, 1], [2, 3], [3, 3], [4, 6], [5, 6]])
plt.scatter(data[:, 0], data[:, 1])

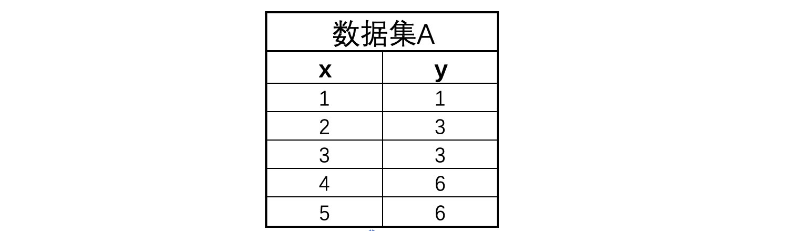
其数据情况 分布如下，横坐标代表数据集特征，纵坐标代表数据集标签。

Step 2： 生成备选规则

CART回归树和分类树流程基本一样，都是逐特征寻找不同取值的中间点作为切分点。对于上述数据集来说，由于只有一个特征，并且总共有5个不同的取值，因此切分点有4个。

y_range = np.arange(1, 6, 0.1)

def plot_scatter_and_line(ax, data, line_position):
    ax.scatter(data[:, 0], data[:, 1])
    ax.plot(np.full_like(y_range, line_position), y_range, 'r--')

line_positions = [1.5, 2.5, 3.5, 4.5]
fig, axes = plt.subplots(2, 2)

for ax, line_position in zip(axes.flatten(), line_positions):
    plot_scatter_and_line(ax, data, line_position)

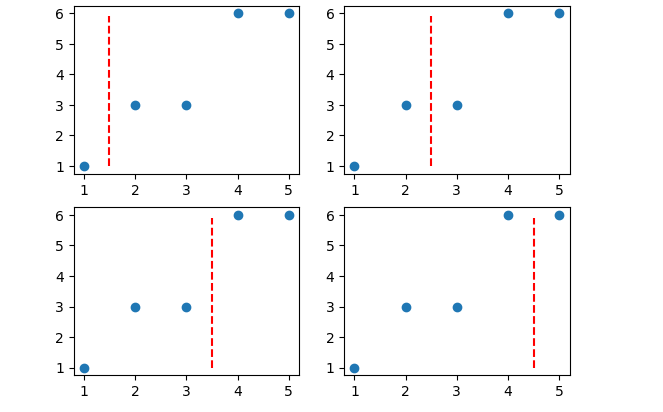
Step 3： 挑选最优切分规则

确定了备选划分规则之后，接下来需要根据某种评估标准来寻找最佳划分方式。

回归树的该步骤和分类树差异较大，分类树中是采用基尼系数或者信息熵来衡量划分后数据集标签不纯度下降情况来挑选最佳划分方式，而在回归树中，则是根据划分之后子数据集MSE下降情况来进行最佳划分方式的挑选。在该过程中，子数据集整体的MSE计算方法也和CART分类树类似，都是先计算每个子集单独的MSE，然后再通过加权求和的方法来进行计算两个子集整体的MSE。

MSE的计算不复杂，但是一个前提是：需要计算MSE，就必须给出一个预测值，然后才能根据预测值和真实值计算MSE。

而CART回归树在进行子数据集的划分之后，会针对每个子数据集给出一个预测值（注意是针对一个子数据集中所有数据给出一个预测值，而不是针对每一个数给出一个预测值），而该预测值会依照让对应子数据集MSE最小的目标进行计算得出，每个子数据集的最佳预测值就是这个子数据集真实标签的均值。

例如对上述第一种划分数据集的情况来说，每个子数据集的预测值和MSE计算结果如下：

plt.scatter(data[:, 0], data[:, 1])
plt.plot(np.full_like(y_range, 1.5), y_range, 'r--')

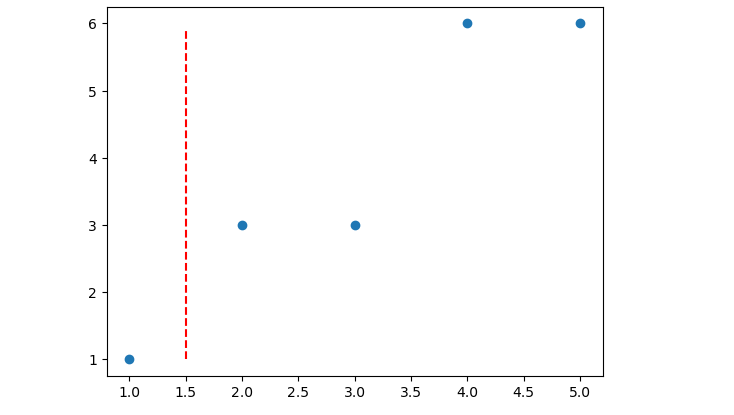
对应划分情况通过如下形式进行表示：

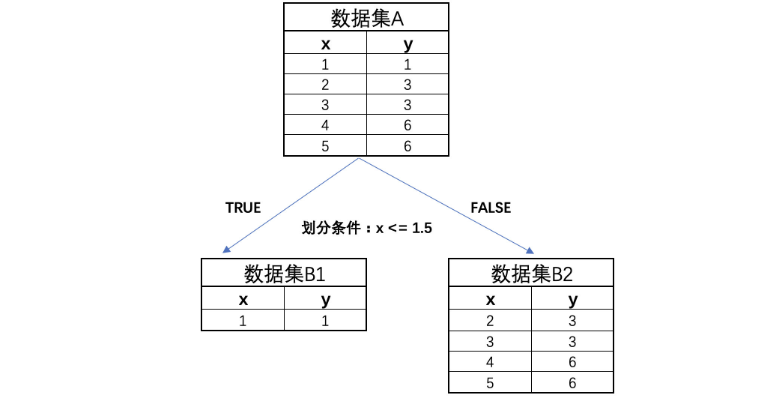
此时计算子数据集B1和B2的MSE，首先是两个数据集的预测值，也就是两个数据集的均值：

# B1数据集的预测值
y_1 = np.mean(data[0, 0])
y_1

# B2数据集的预测值
y_2 = np.mean(data[1: , 1])
y_2

# 模型预测结果
plt.scatter(data[:, 0], data[:, 1])
plt.plot(np.full_like(y_range, 1.5), y_range, 'r--')
plt.plot(np.arange(0, 1.5, 0.1), np.full_like(np.arange(0, 1.5, 0.1), y_1), 'r-')
plt.plot(np.arange(1.7, 5.1, 0.1), np.full_like(np.arange(1.7, 5.1, 0.1), y_2), 'r-')

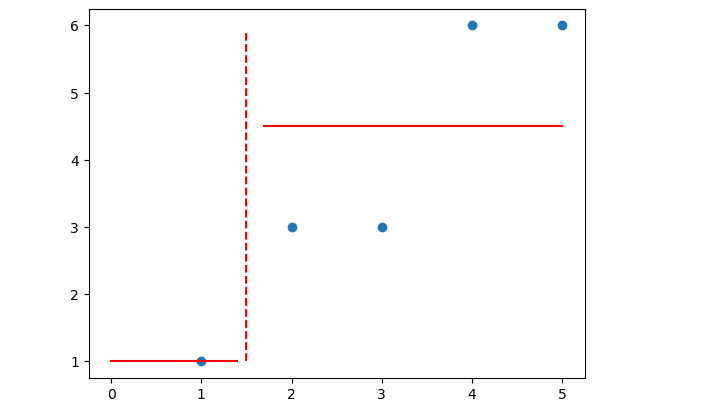
然后计算这种切分规则下，使用MSE作为评估指标的最终Score：

def calculate_mse_reduction(data, split_position):
    # B1数据集的预测值
    y_1 = np.mean(data[0, 0])

    # B2数据集的预测值
    y_2 = np.mean(data[1: , 1])

    # 计算B1的MSE，如果B1只有一个数据点，则MSE为0
    mse_b1 = 0

    # 计算B2的MSE
    mse_b2 = np.power(data[1: , 1] - y_2, 2).mean()

    # 计算B1和B2的加权MSE
    mse_b = 1/5 * mse_b1 + 4/5 * mse_b2

    # 计算父节点的MSE
    mse_a = np.power(data[:, 1] - data[:, 1].mean(), 2).mean()

    # 计算MSE的减少量
    mse_reduction = mse_a - mse_b

    return mse_reduction


mse_reduction = calculate_mse_reduction(data, 1.5)
print(f"MSE reduction: {mse_reduction}")

得到的结果为：MSE reduction: 1.9599999999999993，也就是说，按照这种方式划分后，降低的MSE为：1.9599999999999993。

按照上述过程，计算其他几种划分方式的评分

impurity_decrease = []

for i in range(4):
    # 寻找切分点
    splitting_point = data[i: i+2 , 0].mean()
    
    # 进行数据集切分
    data_b1 = data[data[:, 0] <= splitting_point]
    data_b2 = data[data[:, 0] > splitting_point]
    
    # 分别计算两个子数据集的MSE
    mse_b1 = np.power(data_b1[: , 1] - data_b1[: , 1].mean(), 2).sum() / data_b1[: , 1].size
    mse_b2 = np.power(data_b2[: , 1] - data_b2[: , 1].mean(), 2).sum() / data_b2[: , 1].size
    
    # 计算两个子数据集整体的MSE
    mse_b = data_b1[: , 1].size/data[: , 1].size * mse_b1 + data_b2[: , 1].size/data[: , 1].size * mse_b2
    #mse_b = mse_b1 + mse_b2
    
    # 计算当前划分情况下MSE下降结果
    impurity_decrease.append(mse_a - mse_b)

impurity_decrease

得到的结果如下：[1.9599999999999993, 2.1599999999999993, 3.226666666666666, 1.209999999999999]，也就是说第三种划分情况能够最大程度降低MSE，即此时树模型的第一次生长情况如下：

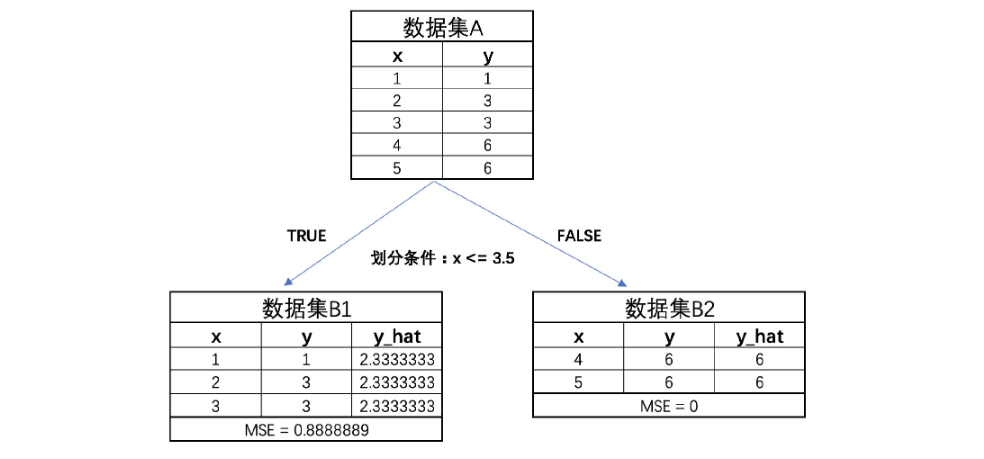
Step 4 ： 进行多轮迭代

接下来，进一步围绕B1和B2进行进一步划分。此时B2的MSE已经为0，因此无需再进行划分，而B1的MSE为0.88，还可以进一步进行划分。

B1的划分过程也和A数据集的划分过程一致，寻找能够令子集MSE下降最多的方式进行切分，得到如下最终图：

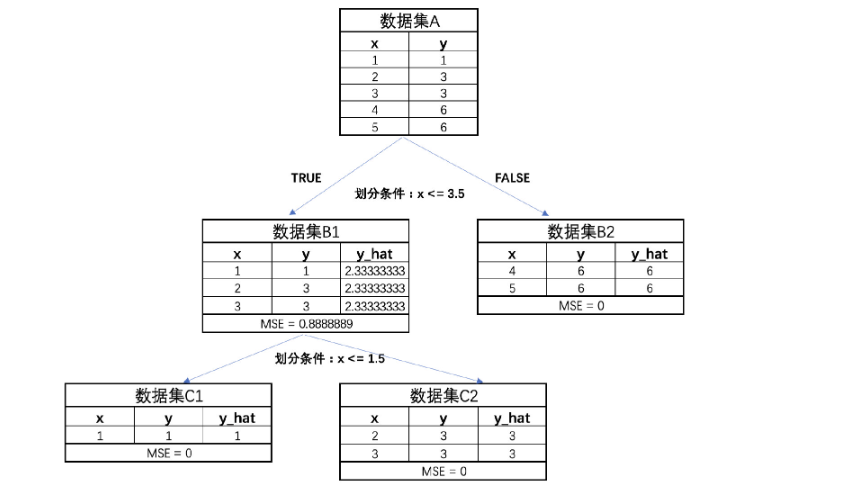
Step 5：构建完成

当模型已经构建完成后，回归树的预测过程其实和分类树非常类似，新数据只要根据划分规则分配到所属样本空间，则该空间模型的预测结果就是该数据的预测结果。

至此，就在这个实验中完成了CART回归树的构建。回归树和分类树的构建过程大致相同、迭代过程也基本一致，可以将其视作同一种建模思想的两种不同实现形式。

3.2 criterion参数的不同取值

CART树虽然能同时解决分类问题和回归问题，但是因为两类问题的性质还是存在一定的差异，因此CART树在处理不同类型问题时相应建模流程也略有不同，所以对应的sklearn中的评估器也是不同的。

回归树单独来看是解决回归类问题的模型，但实际上回归树其实是构建梯度提升树（GBDT）的基础分类器，并且无论是解决回归类问题还是分类问题，CART回归树都是唯一的基础分类器，因此CART回归树的相关方法需要重点掌握，从而为后续集成算法的学习奠定基础。

在Sklearn中实现CART回归树的方法是：DecisionTreeRegressor，在Sklearn中还是通过这种方式来查看：

from sklearn.tree import DecisionTreeRegressor

DecisionTreeRegressor?

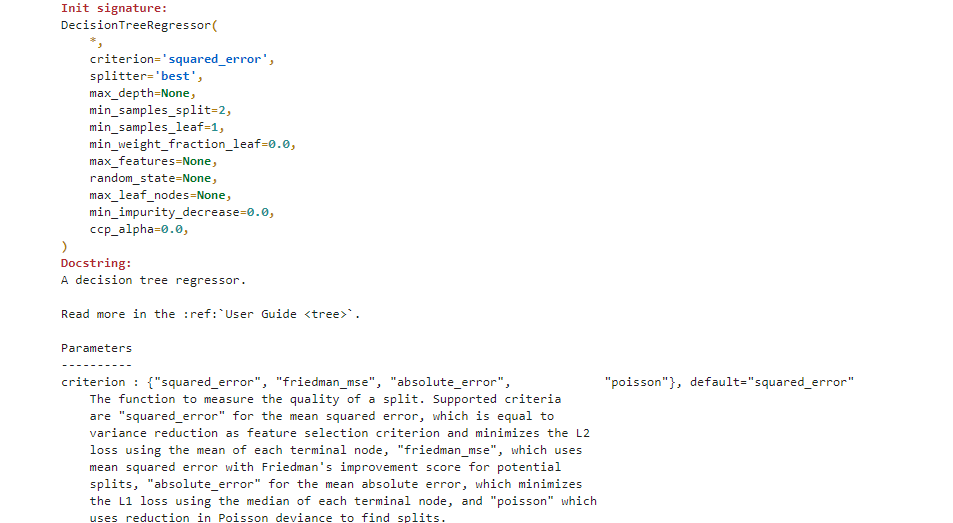
大多数参数都与DecisionTreeClassifier一致，不同 的是：criterion参数，它是备选划分规则的选取指标，对于CART分类树来说默认基尼系数、可选信息熵，但对于CART回归树来说默认mse，同时可选mae、poisson和friedman_mse，针对于不同的取值情况：

• 当criterion='mse’时：

在决策树回归中，如果将评价指标 criterion 设为 mse，就是在使用均方误差（Mean Squared Error，MSE）作为节点分裂的评价标准。计算过程就是误差平方和再除以样本总数，数学表达式如下：
$$MSE=\frac{1}{m}\sum _{i=1}^m(y_i-{\hat{y}}_i{)}^2\text{\hspace{1em}(2)}$$
在这种情况下，决策树会尽可能的使得每个子集的MSE最小。对于决策树的每个叶节点，其预测值是该节点所包含的所有训练样本的目标值的平均值。因为这样的预测值能使得预测值到每个实际值的平方误差之和最小，即最小化MSE。

这也是回归决策树默认的评价指标，因为它对于异常值的敏感度较低，而且具有良好的数学性质，使得计算过程较为简单。

• 当criterion='mae’时：

当在决策树算法中设置评价指标criterion为mae时，使用的是平均绝对误差（Mean Absolute Error，MAE）作为评价标准和，与MSE不同，MAE实际上计算的是预测值和真实值的差值的绝对值再除以样本总数，数学表达如下：
$$MAE=\frac{1}{m}\sum _{i=1}^m|(y_i-{\hat{y}}_i)|\text{\hspace{1em}(3)}$$
在这种情况下，决策树在进行每次分裂时，会尽可能使得每个子集的MAE最小。使MAE最小的预测值并不是平均值，而是中位数。这是因为，对于任意一组数，选择中位数作为预测值可以使得预测值到每个实际值的绝对误差之和最小。

总的来说，MSE是基于预测值和真实值之间的欧式距离进行的计算，而MAE则是基于二者的街道距离进行的计算，很多时候，MSE也被称为L2损失，而MAE则被称为L1损失。当criterion取值为mae时，为了让每一次划分时子集内的MAE值最小，此时每个子集的模型预测值就不再是均值，而是中位数。

CART回归树的criterion不仅是划分方式挑选时的评估标准，同时也是划分子数据集后选取预测值的决定因素。也就是说，对于回归树来说，criterion的取值其实决定了两个方面，其一是决定了损失值的计算方式、其二是决定了每一个数据集的预测值的计算方式——数据集的预测值要求criterion取值最小，如果criterion=mse，则数据集的预测值要求在当前数据情况下mse取值最小，此时应该以数据集的标签的均值作为预测值；而如果criterion=mse，则数据集的预测值要求在当前数据情况下mae取值最小，此时应该以数据集标签的中位数作为预测值。

• 当criterion= ‘friedman_mse’时：

friedman_mse是一种基于mse的改进型指标，是由GBDT（梯度提升树，一种集成算法）的提出者friedman所设计的一种残差计算方法，是sklearn中树梯度提树默认的criterion取值，对于单独的树决策树模型一般不推荐使用。

3.2 Sklearn的调用示例

看下代码：

from sklearn.tree import DecisionTreeRegressor

data = np.array([[1, 1], [2, 3], [3, 3], [4, 6], [5, 6]])

clf = DecisionTreeRegressor().fit(data[:, 0].reshape(-1, 1), data[:, 1])

# 同样可以借助tree.plot_tree进行结果的可视化呈现
plt.figure(figsize=(6, 2), dpi=150)
tree.plot_tree(clf)

结果如下：

单独的树决策树模型一般不推荐使用。

3.2 Sklearn的调用示例

看下代码：

from sklearn.tree import DecisionTreeRegressor

data = np.array([[1, 1], [2, 3], [3, 3], [4, 6], [5, 6]])

clf = DecisionTreeRegressor().fit(data[:, 0].reshape(-1, 1), data[:, 1])

# 同样可以借助tree.plot_tree进行结果的可视化呈现
plt.figure(figsize=(6, 2), dpi=150)
tree.plot_tree(clf)

结果如下：

四、总结

本篇文章主要介绍了在Sklearn库中实现CART分类树和回归树的基本流程。详解了CART分类树的各个参数，包括模型评估类参数、树结构控制类参数以及迭代随机过程控制类参数，并给出了在Sklearn中调用CART分类树的实例。其次，阐述了CART回归树的建模流程和criterion参数的不同取值，也同样提供了Sklearn的调用示例。

最后，感谢您阅读这篇文章！如果您觉得有所收获，别忘了点赞、收藏并关注我，这是我持续创作的动力。您有任何问题或建议，都可以在评论区留言，我会尽力回答并接受您的反馈。如果您希望了解某个特定主题，也欢迎告诉我，我会乐于创作与之相关的文章。谢谢您的支持，期待与您共同成长！