考场错误:
今天是一套neerc的题,难度相对较大,我犯的低级错误比较少,但是对于题目顺序的把握能力,应该提高,尝试去做自己擅长的题目,而不是跟着别人的开题顺序,这样能够更顺畅吧。
经验教训是,构造题,想不出来尽快撤,不要死磕!
Problem C. Connections
这道题目浪费了较长时间
其实很简单,因为题目保证了任意两点之间能够互相到达,所以我们可以通过直接从1开始dfs记录那些边被经过了,再在反图上从1开始dfs,两次走过的边的并集保留,剩下的都可删除,显然这样需要留下的边小于等于2n-2
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int T,n,m;
struct edge
{
int nxt,to,v,fr;
}e[maxn],f[maxn];
int tot,head[maxn],h[maxn];
int vis[maxn],used[maxn];
void add(int x,int y)
{
e[++tot].to=y; e[tot].nxt=head[x]; head[x]=tot; e[tot].fr=x;
f[tot].to=x; f[tot].nxt=h[y]; h[y]=tot;
}
void dfs(int u)
{
for(int i=head[u];i;i=e[i].nxt)
{
int to=e[i].to;
if(!vis[to])
{
vis[to]=1;
used[i]=1;
dfs(to);
}
}
}
void ddfs(int u)
{
for(int i=h[u];i;i=f[i].nxt)
{
int to=f[i].to;
if(!vis[to])
{
vis[to]=1;
used[i]=1;
ddfs(to);
}
}
}
int main()
{
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&m); tot=0;
for(int i=1;i<=m;i++) h[i]=head[i]=vis[i]=used[i]=0;
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
}
dfs(1);
for(int i=1;i<=n;i++) vis[i]=0;
ddfs(1);
int gs=m-2*n;
for(int i=1;i<=tot && gs;i++)
{
if(!used[i])
{
printf("%d %d\n",e[i].fr,e[i].to);
gs--;
}
}
}
return 0;
}Problem A. Archery Tournament
这道题目的重点是发现对于一个横坐标来说,最多有log级别的圆与它相交,证明可以根据相切的情况是极限,是1/4即可,说明如下:
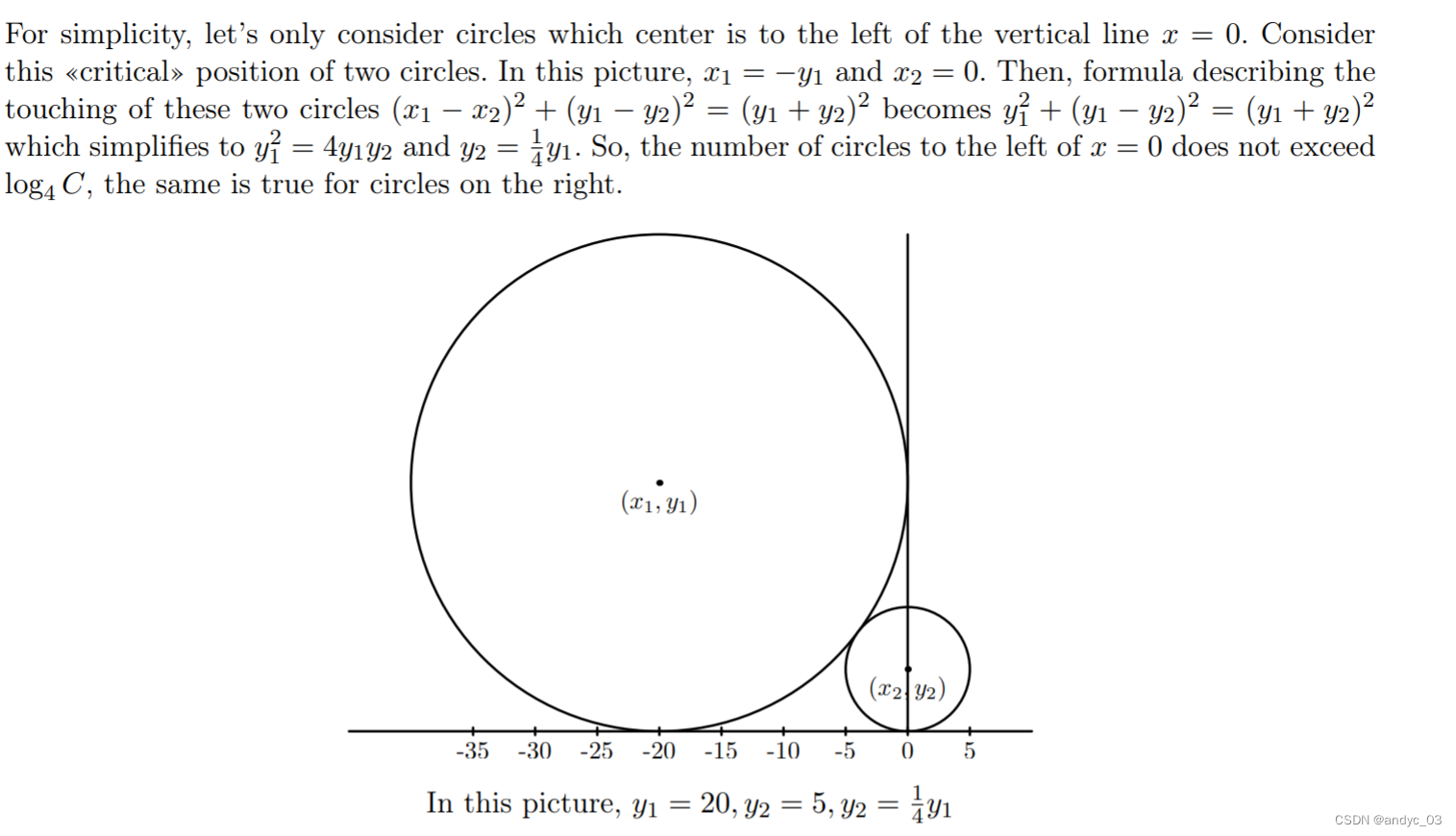
那么我们需要做的就是把一个区间[x-r,x+r]内,打上这个圆的编号,然后查询时,访问这一点的所有圆即可
可以通过线段树维护set暴力地实现!
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;
const int inf=1e9;
set <int> tr[maxn<<5];
int ls[maxn<<5],rs[maxn<<5],tot;
int n,px[maxn],R[maxn];
void update(int &u,int l,int r,int L,int R,int id,int flag)
{
if(!u) u=++tot;
if(L>r || R<l) return;
if(l>=L && r<=R)
{
// cerr<<l<<" "<<r<<endl;
if(flag==1) tr[u].insert(id);
else tr[u].erase(id);
return;
}
int mid=l+r>>1;
if(L<=mid) update(ls[u],l,mid,L,R,id,flag);
if(mid<R) update(rs[u],mid+1,r,L,R,id,flag);
}
ll sqr(int x)
{
return 1ll*x*x;
}
int query(int u,int l,int r,int x,int y)
{
// cerr<<u<<" "<<l<<" "<<r<<endl;
if(!u) return -1;
if(l<=x && x<=r)
{
for(auto iter=tr[u].begin();iter!=tr[u].end();iter++)
{
// cerr<<x<<" "<<y<<" "<<*iter<<endl;
if(sqr(x-px[*iter])+sqr(y-R[*iter])<sqr(R[*iter]))
return *iter;
}
// return;
}
int mid=l+r>>1;
if(x<=mid) return query(ls[u],l,mid,x,y);
else return query(rs[u],mid+1,r,x,y);
}
int main()
{
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
scanf("%d",&n);
int rt=0;
for(int i=1;i<=n;i++)
{
int op,x,y;
scanf("%d%d%d",&op,&x,&y);
if(op==1)
{
px[i]=x; R[i]=y;
update(rt,-inf,inf,x-y,x+y,i,1);
// cerr<<tot;
// cerr<<ls[1]<<" "<<rs[1]<<endl;
}
else
{
int id=query(rt,-inf,inf,x,y);
if(id==-1)
printf("-1\n");
else
{
printf("%d\n",id);
update(rt,-inf,inf,px[id]-R[id],px[id]+R[id],id,-1);
}
}
}
return 0;
}Problem D. Designing the Toy
不妨设a<=b<=c
首先,我们发现但ab<c一定无法构造,这样我们就可以使用
构造方式就是全部放在z=0平面上,那么我们放a个在对角线上,剩下b-a个放在最后一个对角线上的点再接着向上延伸,c-a-b的点放在矩形围成的剩余位置

具体实现时,不同的轴的对应关系很难受,调了很久,,,
#include<bits/stdc++.h>
using namespace std;
int a,b,c;
pair <int,int> val[4];
int p[1005][4];
int cnt,G[105][105],X,Y,Z;
void add(int x,int y,int z)
{
p[++cnt][X]=x; p[cnt][Y]=y; p[cnt][Z]=z;
}
void work(int A,int B,int C)
{
int tot=0;
A--; B--;
while(tot<=A)
{
add(tot,tot,0);
G[tot][tot]=1;
tot++;
}
while(tot<=B)
{
add(A,tot,0);
G[A][tot]=1;
tot++;
}
// for(int i=0;i<A;i++)
// {
// if(C==tot) break;
// for(int j=0;j<=B;j++)
// {
// if(C==tot) break;
// if(!G[i][j])
// {
// G[i][j]=1;
// add(i,j,0);
// tot++;
// }
// }
// }
for(int i=0;i<=A;i++)
{
if(C==tot) break;
for(int j=0;j<=B;j++)
{
if(C==tot) break;
if(!G[i][j])
{
G[i][j]=1;
add(i,j,0);
tot++;
}
}
}
}
void dw(int x,int y,int z)
{
X=x; Y=y; Z=z;
}
int main()
{
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
scanf("%d%d%d",&a,&b,&c);
val[1]=make_pair(a,1); val[2]=make_pair(b,2); val[3]=make_pair(c,3);
sort(val+1,val+4);
if(val[3].first>val[1].first*val[2].first)
{
printf("-1\n");
return 0;
}
if(a>=b && a>=c)
{
if(b>=c)
dw(1,0,2),work(c,b,a);
else
dw(0,1,2),work(b,c,a);
}
else if(b>=a&&b>=c)
{
if(a>=c)
dw(2,0,1),work(c,a,b);
else
dw(0,2,1),work(a,c,b);
}
else if(c>=a&&c>=b)
{
if(a>=b)
dw(2,1,0),work(b,a,c);
else
dw(1,2,0),work(a,b,c);
}
// cerr<<X<<" "<<Y<<" "<<Z;
printf("%d\n",cnt);
for(int i=1;i<=cnt;i++)
{
for(int d=0;d<3;d++)
printf("%d ",p[i][d]);
printf("\n");
}
return 0;
}Problem G. The Great Wall
首先观察到答案求的是第k大的方案,可以二分答案,问题转变为求<=mid的方案数
这道题目我们考虑初始的贡献是ai的和,然后我们考虑两个线段的影响,
case1 如果两个线段不相交
那么就是两段bi-ai的和,我们枚举第一段的位置,第二段的和的大小和位置都有要求相当于二维数点问题,在O(nlogn)内可以解决
case 2 如果两个线段相交
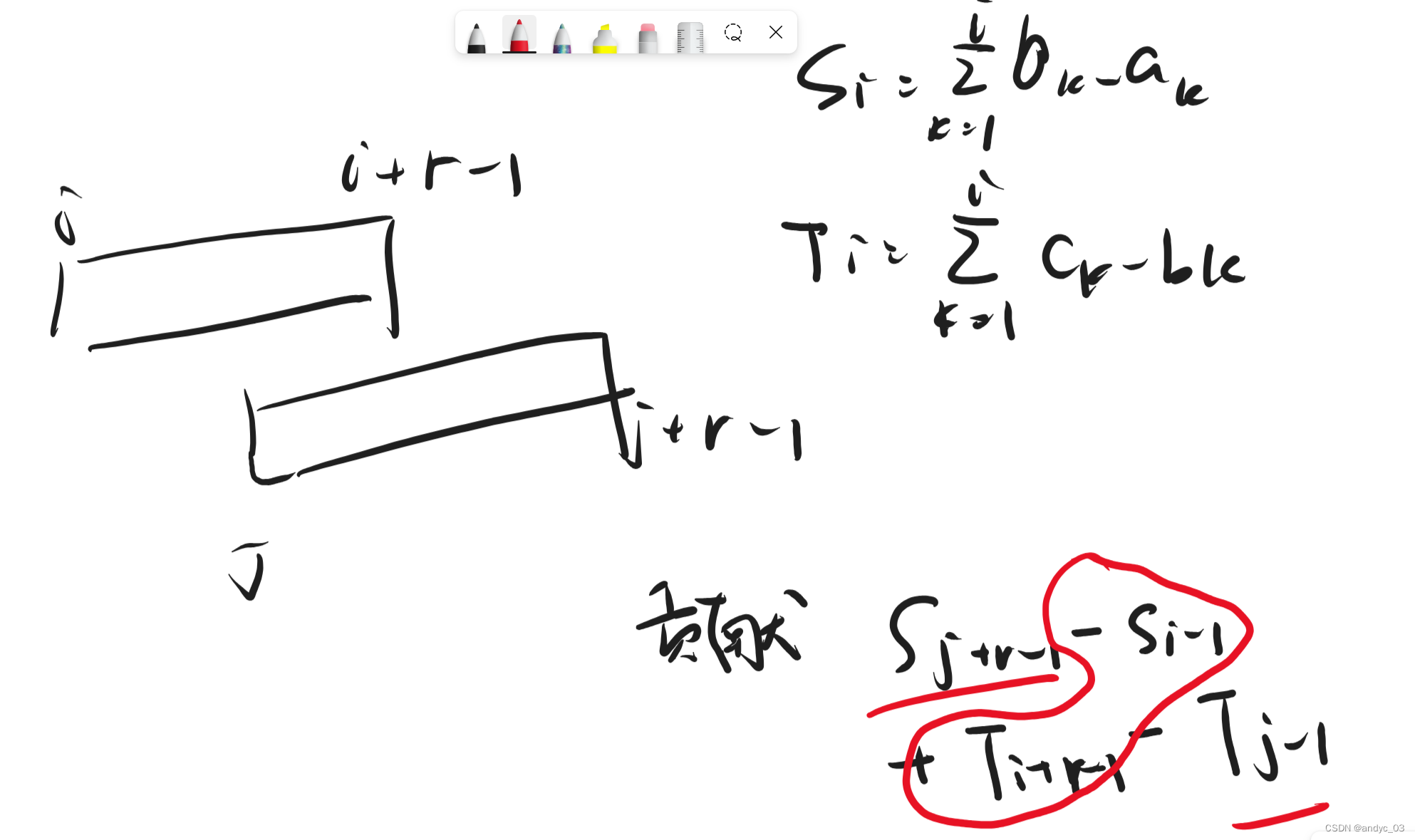
这样总的复杂度就是两个log
代码待补


![[MySql]JDBC编程](https://img-blog.csdnimg.cn/3761fcb922ee49ecaa14063c05dbb149.png)