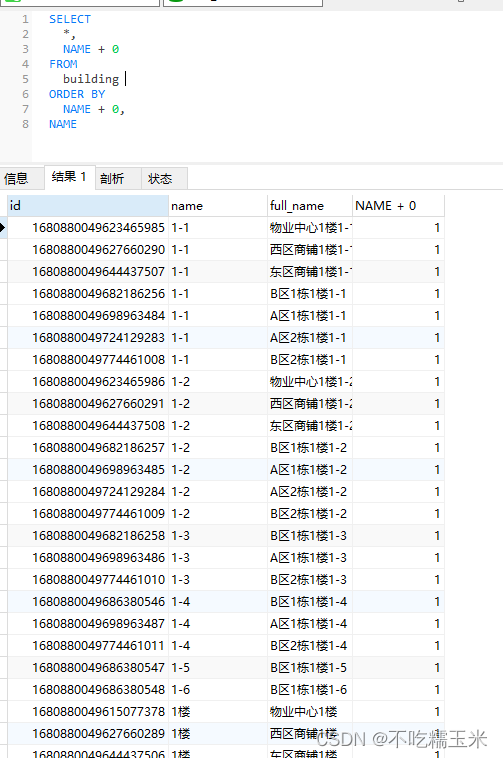
0 上周回顾

上周完成了RTM的研究学习, 完成了进一步阅读论文所需的知识储备.
同时从代码层面深度解析了正演和RTM存在的关系, 发掘了很多富有参考意义的信息.

1 本周计划

深度剖析论文《Deep-Learning Full-Waveform Inversion Using Seismic Migration Images》的方法体系, 构思复现的可能 (但是不一定真要去复现), 探索RTM在实际DL-FWI中的应用潜力.

2 完成情况

简单来说, 这篇的论文主要分为两大部分: 首先是准备背景速度, 其次是训练迭代网络. 原文中提供了如下的伪代码来描述:

2.1 算法流程: 准备背景速度

输入到算法中的变量有两个, 一个是观测数据 (${\mathbf{P}}_{\text{obs}}$), 一个是偏移速度模型 ${\mathbf{m}}_{\text{mig}}$, 其实就是初始速度模型. 这个初始模型是基于目标速度模型的速度变化生成的一个线性的增长的层次图像.

For example, our approach uses the linearly increasing velocity model along the depth direction from 1500 to 2500 m/s as the migration velocity model in the following experiments. As a result, our proposed approach does not rely on a good starting (migration) model.

Fig1. 论文中给出的观测数据图像 (实际上就是共源炮集地震数据)

Fig2. 偏移速度模型, 或者说初始速度模型

然后作者基于这个初始速度模型作为基础的背景, 以及观测信息提供的地震资料得到RTM图像, 因为观察信息有15个炮集, 因此这里RTM也有15张. 这里对应伪代码中的 “Compute the prestack RTM image $\mathbf{I}({\mathbf{m}}_{\text{mig}})$”

而后, 将15个张RTM图像和初始速度模型 “按照通道维度拼接在一起”, 形成通道数为16的图像集 (因为RTM和速度模型的维度一致, 可以这么做), 输入到已经训练完备的网络${\Gamma }_{\theta }(\cdot )$中, 这个网络如下图:

Fig3. 论文中提到的第一个类U-Net网络结构

显而易见, 这个网络用的U-Net结构. 因为这里输入和输出的图像尺寸是一致的, 而且大小变化都是显而易见的x2和÷2的变化, 因此作者没有必要表明尺寸参数, 一定不要误以为这里都是针对向量的操作. (因为我最开始拿到这篇论文一瞟的时候, 我 就是这么认为的). 这其实算是表现了网络的灵活性.
这个网络有些残差网络的味道, 最后在输出1通道的图像后, 他将初始速度模型${\mathbf{m}}_{\text{mig}}$和这个图像进行了求和, 最终得到了背景速度${\mathbf{m}}_{\text{back}}$. 这就是伪代码里面的${\mathbf{m}}_{\text{back}}={\Gamma }_{\theta }[{\mathbf{m}}_{\text{back}},\mathbf{I}({\mathbf{m}}_{\text{mig}})]$的含义.

其实想一想也就说得通了, 作者为什么在论文多称这个初始速度模型为 “Migration velocity model” 而不是 “Initial velocity model”. 因为这个图像本身没有速度模型的基本结构 (Fig2 展示了它是一个通用图像), 而是需要与另一个网络的输出求和才能得到目标速度模型, 因此自身更像是一个 “偏移量”, 需要与一个 “基准” 结合才能得到目标.

那么这个网络${\Gamma }_{\theta }(\cdot )$是怎么训练呢? 通过阅读, 我感觉应该是在算法启动之前就要训练好. 原文的公式15给出了计算损失函数的公式:
$$L_3=\frac{1}{2}{\Vert {\mathbf{m}}_{\text{back }}-{\mathbf{Sm}}_{\text{true }}\Vert }_2^2,{\mathbf{m}}_{\text{back }}={\Gamma }_{\theta }\left[{\mathbf{m}}_{\text{mig }},\mathbf{I}\left({\mathbf{m}}_{\text{mig }}\right)\right]$$
可见, 用的是MSE, 但是这个$\mathbf{S}$是什么呢? 这是一个高斯算子, 用来平滑的. 怎么平滑呢?

$\mathbf{S}$ is a smoothed operator to remove the high wavenumber component of the true velocity model. We apply a Gaussian smoothing filter to the true velocity model. There are a total of 30 times repeated filter applications. The standard deviation of the Gaussian function is 5. The window size of the filter is 5 × 5. It has to be noted that the principle of smoothing the velocity model is that we should remove the high wavenumber component and the resulting background model can guarantee correct kinematic behavior.

${\mathbf{Sm}}_{\text{true}}$含义就是用了一个标准差为5, 滤波器窗口为5×5的高斯算子$\mathbf{S}$作用于标准的速度模型${\mathbf{m}}_{\text{true}}$, 并且反复作用30次.
在担心这样会不会使得速度模型糊得太离谱, 于是我自己试了下, 大概就是这种差距↓ 感觉…还行√

Fig4. 左图为原速度模型, 右图为高斯平滑后的目标

简单来说, 我们第一个网络${\Gamma }_{\theta }$的学习目标是得到比较模糊的基础速度背景:

• 是一个从${\mathbf{m}}_{\text{mig}}$ 到 ${\mathbf{m}}_{\text{back}}$ 的改变
• 是从一个"投至四海皆准"的通用的初始速度 (Fig2) 到 与 真实速度模型有着类似运动学构造的模糊地层结构 (Fig4 右)

所以这个网络${\Gamma }_{\theta }$的目标是找方向, 而不是一锤定音的东西.

得到${\mathbf{m}}_{\text{back}}$之后, 紧接着基于这个背景, 再度进行一次RTM得到 ${\mathbf{I}}_i({\mathbf{m}}_{\text{back}})$, 因为观察数据有15个通道, 因此这里${\mathbf{I}}_i({\mathbf{m}}_{\text{back}})$也有15个.
这里我们讨论的都是叠前RTM图像, 因此这些图像可以进行叠加, 这里作者的叠加手段就是将这里的15张图像全部加在一起, 从而得到叠加的RTM图像:
$${\mathbf{I}}_{\text{stack }}=\sum _{i=1}^{ns}{\mathbf{I}}_i$$
这里就囊括了伪代码中的如下几步:

2.2 算法流程: 迭代神经网络

通过第一步的操作, 我们现在手上有那些已知的关键信息?

• 观察信息${\mathbf{P}}_{\text{obs}}$ (已用不上)
• 初始速度模型${\mathbf{m}}_{\text{mig}}$ (已用不上)
• ${\mathbf{I}}_0({\mathbf{m}}_{\text{back}})$ … ${\mathbf{I}}_{14}({\mathbf{m}}_{\text{back}})$
• ${\mathbf{I}}_{\text{stack}}({\mathbf{m}}_{\text{back}})$
• ${\mathbf{m}}_0$ (其实就是${\mathbf{m}}_{\text{back}}$)

然后这里将引入作者介绍的迭代神经网络${\Lambda }_{\theta }^k$(·), 它的结构如下:

Fig5. 第二个网络结构 这个网络结构非常小, 它的输入是由四个图像结构按照通道拼接而成, 其用公式可表示为:

$${\mathbf{m}}_{k+1}={\Lambda }_{\theta }^k[{\mathbf{m}}_k,\mathbf{I}({\mathbf{m}}_{\text{back}}),{\mathbf{I}}_{\text{stack}}({\mathbf{m}}_{\text{back}}),\nabla \psi ({\mathbf{m}}_k)],k=0,1,\dots ,N-1$$
这里的前三者都是已知的, 但是$\nabla \psi ({\mathbf{m}}_k)$可能有点生疏, 通过作者介绍, 这里是Dirichlet energy的表示, 即
$$\psi ({\mathbf{m}}_k)=\frac{1}{2}\mid \mid \nabla \mathbf{m}\mid {\mid }_2^2$$
因此$\nabla \psi ({\mathbf{m}}_k)$可以表示为${\nabla }^{\ast }(\nabla {\mathbf{m}}_k)$.
但是这里在代码中我不确定怎么表示, $m$是当前迭代的速度模型, 但是它的梯度可以通过确定的手段得到吗? 这我有点疑问和不确定.
但是总的来说, 输入部分应当是清晰的, 我们将他们打包为通道数为1+15+1+1 = 18的图集输入到网络中.
这里依旧使用了残差的手段, 网络直接输出部分加上了当前迭代的速度模型${\mathbf{m}}_k$之后才进行的输出.
然后输出的结果还会作为作为下一回合循环的输入部分${\mathbf{m}}_{k+1}$, 这个输入部分和已有信息再通过1+15+1+1形成新的18通道的输入, 如此就构成了循环结构, 这个循环结构会执行$N$次 (作者设定的$N=10$)

这个过程当中, 并没有求导和逆向传播, 这就很有意思了. 而是在循环最后一轮, 通过最终的${\mathbf{m}}_{N-1}$来进行Loss计算, 公式如下:

$$L_4=\frac{1}{2}{\Vert {\Lambda }_{\theta }^N(\mathbf{B})-{\mathbf{m}}_{\text{true }}\Vert }_2^2,\mathbf{B}=[{\mathbf{m}}_{N-1},\mathbf{I}({\mathbf{m}}_{\text{back}}),{\mathbf{I}}_{\text{stack}}({\mathbf{m}}_{\text{back}}),\nabla \psi ({\mathbf{m}}_{N-1})]$$

仍然是MSE, 而且这次我们不再拟合平滑后的速度模型了, 而是直接向真实的速度模型靠拢. 如果说${\Gamma }_{\theta }$的学习目标是得到比较模糊的基础速度背景, 那么${\Lambda }_{\theta }^N$网络就是彻底得到高清的速度模型. 它不再是从${\mathbf{m}}_{\text{mig}}$ 到 ${\mathbf{m}}_{\text{back}}$ 的改变, 而是:

• 是一个从${\mathbf{m}}_{\text{back}}$ 到 ${\mathbf{m}}_{\text{ture}}$ 的改变
• 是从一个与真实速度模型有着类似运动学构造的模糊地层结构(Fig4 右) 到 刻画细致的高清地层图(Fig4 左)

最终, 不妨想想, 这个网络真的小吗? 其实一次循环完后他并没有求导, 如果我们将一次forward的持续时间规定为遇到求导即为结束的话, 那么循环在持续的话网络就没有结束, 因此, 这里作者设置的${\Lambda }_{\theta }^N$实际很长, 应该有接近30多层. 但又因为通道数不大, 因此学习的参数量应该不会很大.

上述这就是伪代码中后续部分的含义:

3 存在的主要问题

方法理清楚是这么个理.
但是站在代码复现角度, 仍然有些疑惑, 我感觉是读完论文没能完全搞清楚的

1. 第二个网络中的输入参数$\nabla \psi ({\mathbf{m}}_k)={\nabla }^{\ast }(\nabla {\mathbf{m}}_k)$究竟如何用代码来复现呢? 这篇论文并没有公布源码, 只是提供了一个关键词 “Dirichlet energy”. 这里的正则项$\psi ({\mathbf{m}}_k)$正是来源于这个东西, 它本身又表示为: $\psi ({\mathbf{m}}_k)=\frac{1}{2}\mid \mid \nabla \mathbf{m}\mid {\mid }_2^2$. 我觉得要了解这个之前需要学习一下Dirichlet energy的含义.
2. 本文我用橙色地方标注了一句话: “以及观测信息提供的地震资料得到RTM图像”. 作者这里直接就通过观测信息${\mathbf{P}}_{\text{obs}}$, 即多炮的共源炮集图像直接作为了RTM的资料, 这似乎没有解决我之前认识RTM的过程中提出的疑惑.
   之前我尝试做RTM的时候, 一次互相关构建需要所有时刻的波场快照, 而现场我们只能得到一炮释放后固定位置接收器接收到的共源炮集图像, 按照我的思路, 没法仅仅依靠后者得到RTM图像. 而这里作者是只通过后者得到的, 这和我的思路有出入.
   我只能猜测两种解释:
   • 在 仅仅 已知接收器获取的共源炮集图像 (就是长得像山峰那样的图像) 且 不知道全时刻的波场快照的情况下, 是可以直接得到RTM图像的.
   • 共源炮集图像 可以推到出 全时刻的波场快照.

关于第二个问题, 作者在文中引出了它采用的生成RTM图像的方法:

Here, we apply an inverse scattering imaging condition to produce the RTM image, for a common source recording, which can be formulated mathematically as [39]

作者采用了 “inverse scattering imaging condition” 来生成RTM图像, 作者也给出了相关论文的支撑.

[39] H. Douma, D. Yingst, I. Vasconcelos, and J. Tromp, “On the connection between artifact filtering in reverse-time migration and adjoint tomography,” Geophysics, vol. 75, no. 6, pp. 219–223, 2010

也许这里面会有答案.

4 下一步工作

为了获得更多启示, 接下来会尝试读论文《On the connection between artifact filtering in reverse-time migration and adjoint tomography》, 但是这篇文章数学公式有亿点多, 可能有点 hard to follow … 所以不见得马上能搞懂, 做长远打算吧.
更多来看, 我可能会接触点其他DL-FWI的论文.
有可能是经典VelocityGAN: 《Data-driven seismic waveform inversion A study on the robustness and generalization》, 这个挺好, 有源码, 但是时间有点早了, 是2020.
或者是 《Multiscale data-driven seismic full-waveform inversion with field data study》, 用自然图像做DL-FWI, 很有想法, 时间略近一点, 2021, 但是好像没有源码.
多看论文才有idea, 先不急着卡在RTM这里.