机器学习实战：Python基于Ridge岭回归进行正则化（十三）

文章目录

- 1.前言
- - 1.1 岭回归的介绍
  - 1.2 岭回归的应用
- 2.自定义数据集实战演示
- - 2.1 导入函数
  - 2.2 创建数据集
  - 2.3 alpha=0、1、10、100的分别情况
- 3.Dushanbe_house数据集实战演示
- - 3.1 导入函数和数据
  - 3.2 剔除空值及可视化
  - 3.3 整理数据
  - 3.4 训练和测试数据集
  - 3.5 评估数据集
- 4.讨论

1.前言

1.1 岭回归的介绍

岭回归（Ridge Regression）是一种常用的线性回归方法，用于处理具有共线性（collinearity）问题的数据集。在普通最小二乘线性回归中，如果自变量之间存在高度相关性，会导致估计的回归系数不稳定，甚至无法准确估计。岭回归通过引入一个正则化项来解决这个问题。

岭回归的关键思想是在最小二乘目标函数中添加一个L2正则化项，该项对回归系数进行惩罚。这个正则化项是通过对回归系数的平方和进行惩罚，乘以一个调节参数alpha。当alpha为0时，岭回归等效于普通最小二乘回归；而当alpha趋近于无穷大时，回归系数趋近于0。因此，岭回归通过控制alpha的取值，平衡了回归系数的拟合能力和稳定性。

优点：

解决共线性问题：岭回归能够有效降低多重共线性对回归系数估计的影响。在存在高度相关的自变量的情况下，岭回归可以提供更稳定和可靠的回归系数估计。
可控制的正则化参数：通过调节正则化参数alpha的取值，可以控制模型的拟合程度和回归系数的收缩程度。这使得岭回归具有灵活性，可以根据具体问题和数据来平衡模型的复杂性和拟合能力。
适用于高维数据：当数据集中存在大量自变量或特征时，岭回归可以提供更稳定的回归系数估计。它通过控制回归系数的大小来减少对噪声和不相关特征的过度拟合，从而提高模型的泛化能力。

缺点：

引入偏差：岭回归通过对回归系数进行惩罚，可能引入一定的偏差。正则化项的存在会导致回归系数的估计偏离普通最小二乘估计，可能造成一定的信息损失。
需要设置正则化参数：岭回归的性能受到正则化参数alpha的影响。选择合适的alpha值需要一定的经验或调参过程。过大或过小的alpha值可能导致模型性能下降或过拟合的问题。
不具备特征选择能力：与Lasso回归相比，岭回归不具备显式的特征选择能力。它对所有的自变量都进行了收缩，而不会将某些系数缩减到零。因此，在需要进行特征选择的情况下，Lasso回归可能更适合。

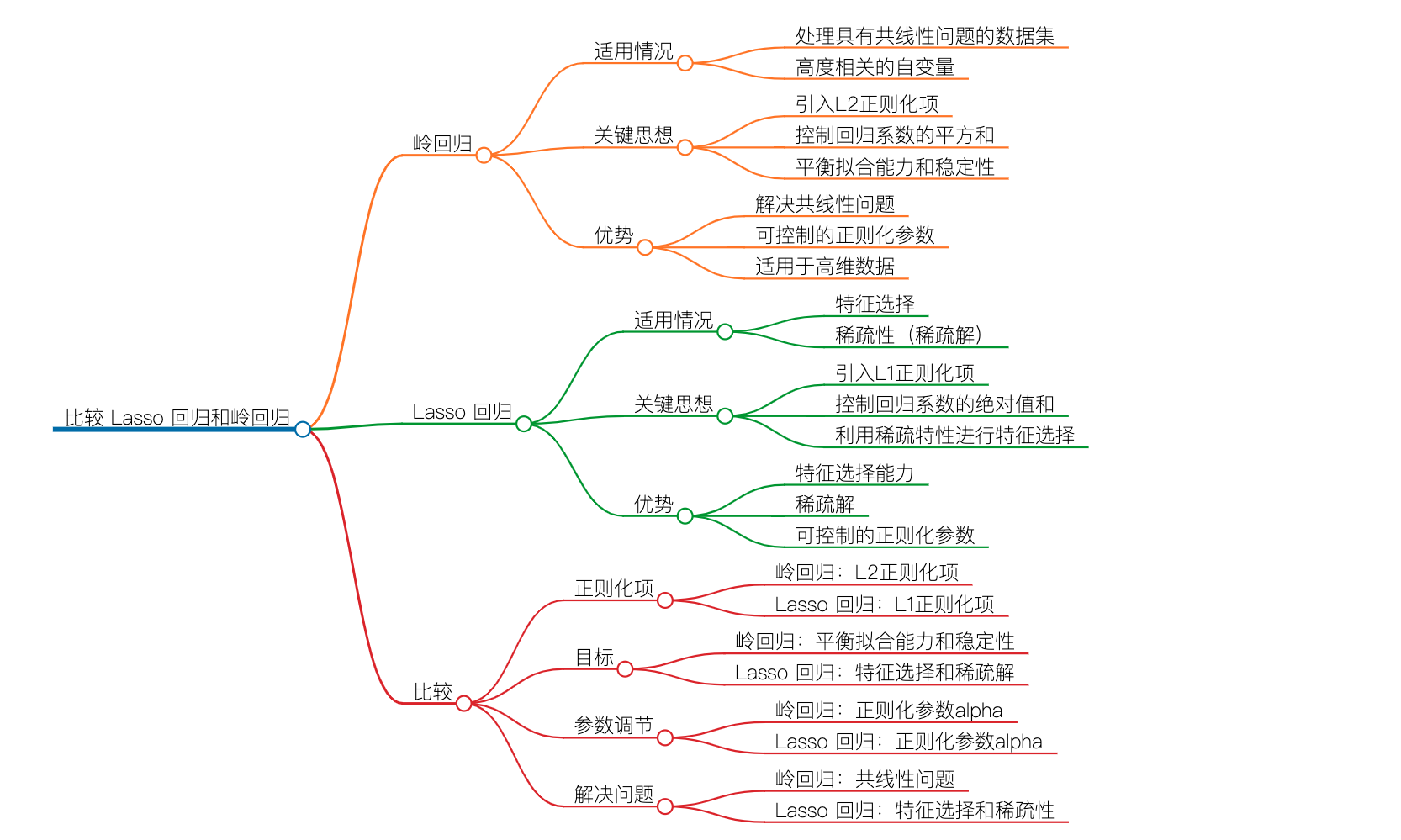
一张图看懂LASSO回归和岭回归

1.2 岭回归的应用

经济学和金融学：岭回归可用于建立资产定价模型、预测经济指标、研究金融市场的因素影响等。在金融领域，岭回归可以帮助识别并分析相关因素对金融市场和资产价格的影响。
医学和生物学：岭回归可应用于医学和生物学领域中的数据分析和预测任务。例如，在基因表达分析中，岭回归可以帮助识别与特定疾病或生物过程相关的基因，并预测基因表达与相关结果之间的关系。
社会科学：岭回归可用于社会科学领域中的数据分析和建模，如人口统计学、社会经济学、心理学等。它可以帮助研究人口特征、社会经济指标等与特定社会现象或行为之间的关联性。
工程和物理学：岭回归在工程和物理学领域中也有广泛应用。例如，在信号处理中，岭回归可用于信号恢复和噪声滤波任务。在材料科学中，岭回归可用于建立材料性能与各种特征参数之间的关系模型。
数据分析和预测：由于岭回归在处理多重共线性和高维数据方面的优势，它在数据分析和预测任务中被广泛使用。岭回归可以帮助建立准确和稳定的预测模型，适用于各种应用领域，如销售预测、市场分析、房地产估价等。

2.自定义数据集实战演示

2.1 导入函数

from sklearn.datasets import make_regression
from matplotlib import pyplot as plt
import numpy as np
from sklearn.linear_model import Ridge

2.2 创建数据集

A, b, coefficients = make_regression(
    n_samples=50,
    n_features=1,
    n_informative=1,
    n_targets=1,
    noise=5,
    coef=True,
    random_state=1
)

2.3 alpha=0、1、10、100的分别情况

当alpha等于0时，岭回归退化为最小二乘法（Ordinary Least Squares, OLS）回归。在岭回归中，正则化项的系数为0，不会对回归系数施加任何约束或惩罚。

alpha = 0
n, m = A.shape

I = np.identity(m)
w = np.dot(np.dot(np.linalg.inv(np.dot(A.T, A) + alpha * I), A.T), b)
plt.scatter(A, b)
plt.plot(A, w*A, c='red')

## w = array([89.22901347]）

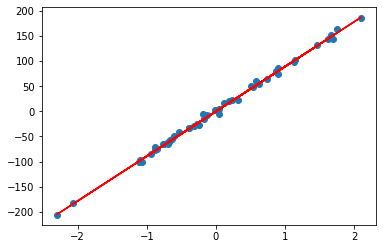
alpha=1时：

rr = Ridge(alpha=1)
rr.fit(A, b)
w = rr.coef_
print(w)
## Output w = array([87.39928165])

plt.scatter(A, b)
plt.plot(A, w*A, c='red')

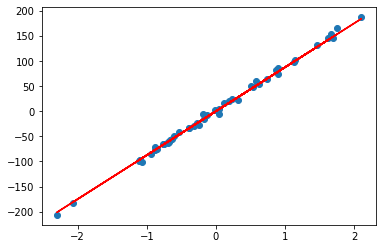
alpha=10时：

rr = Ridge(alpha=10)
rr.fit(A, b)
w = rr.coef_
print(w)
## Output w = array([73.60064637])

plt.scatter(A, b)
plt.plot(A, w*A, c='red')

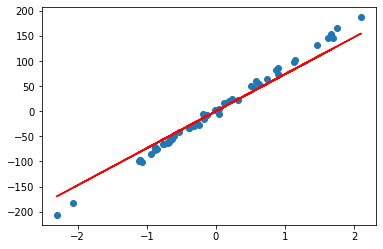
alpha=100时：

rr = Ridge(alpha=100)
rr.fit(A, b)
w = rr.coef_
print(w)
## Output w = array([28.54061056])

plt.scatter(A, b)
plt.plot(A, w*A, c='red')

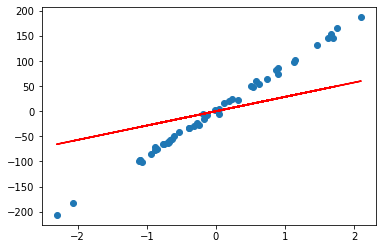
不难理解，当alpha值较大时，正则化项对回归系数的惩罚力度增加，使得回归系数更接近于零。回归线的斜率接近于零意味着预测函数对输入特征的影响减小，因此回归线可以看作是在整个数据集上取平均值为零的平面。这样可以有效地最小化不同数据集之间的方差。

通过增加alpha值，岭回归模型会更强调对训练数据整体的拟合，并减小对特定样本或异常值的过度拟合。这样可以提高模型的泛化能力，使其对新数据的预测更稳定，并减少模型在不同数据集上的变化。

3.Dushanbe_house数据集实战演示

3.1 导入函数和数据

import io
import urllib3
import pandas as pd


http = urllib3.PoolManager()
r = http.request('GET', 'https://hands-on.cloud/wp-content/uploads/2022/04/Dushanbe_house.csv')
Dushanbe = pd.read_csv(io.StringIO(r.data.decode('utf-8')))

# 查看数据示例
Dushanbe.head()

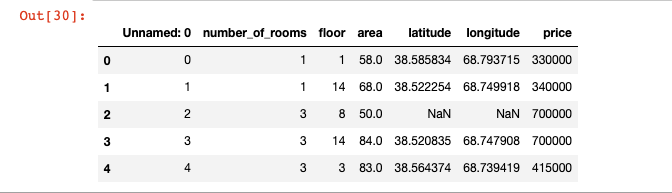
3.2 剔除空值及可视化

# 删除空值
Dushanbe.dropna(axis=0, inplace=True)

# 如果存在空值，显示空值数量
Dushanbe.isnull().sum()

# 使用 plotly.express 导入模块
import plotly.express as px

# 绘制三维散点图
fig = px.scatter_3d(Dushanbe, x='number_of_rooms', y='area', z='price',
                    color='price')
fig.show()

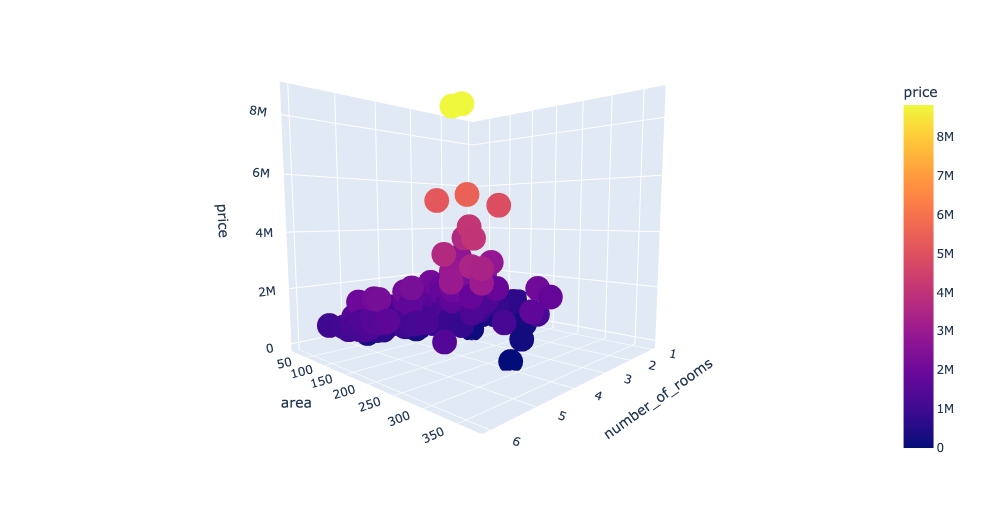
3.3 整理数据

# 提取数据集的列名
columns = Dushanbe.columns

# 存储输入和输出变量
Inputs = Dushanbe[columns[0:-1]]  # 输入变量
outputs = Dushanbe[columns[-1]]  # 输出变量

3.4 训练和测试数据集

from sklearn.model_selection import train_test_split

# 导入模块
from sklearn.model_selection import train_test_split

# 拆分训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(Inputs, outputs, test_size=0.3, random_state=42)

# 导入 Ridge 模型
from sklearn.linear_model import Ridge
# 设置 alpha 参数为 0.9 并初始化 Ridge 回归模型
model = Ridge(alpha=0.9)
# 使用训练数据拟合 Ridge 回归模型
model.fit(X_train, y_train)

# 预测
y_pred = model.predict(X_test)

3.5 评估数据集

from sklearn.metrics import r2_score
print('R-square score is:', r2_score(y_test, y_pred))
## R-square score is : 0.3787461308826928

import matplotlib.pyplot as plt
# 设置图形大小
plt.figure(figsize=(15, 8))
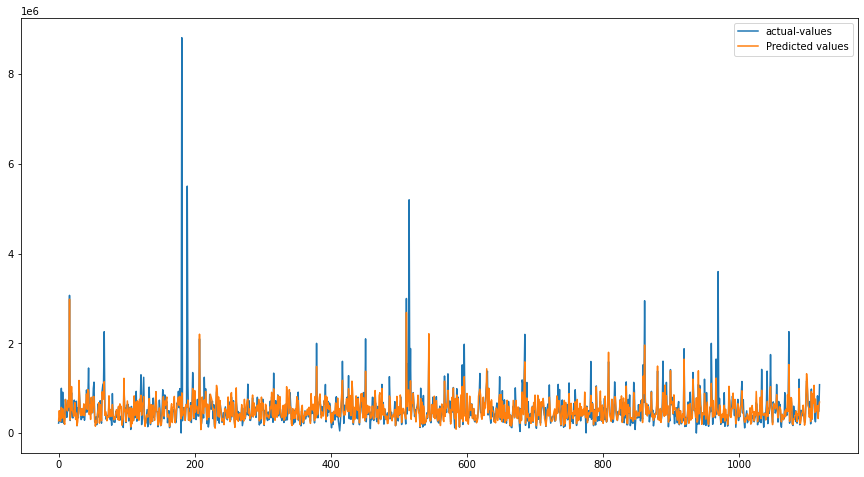
# 绘制实际值和预测值的图形
plt.plot([i for i in range(len(y_test))], y_test, label="实际值")
plt.plot([i for i in range(len(y_test))], y_pred, label="预测值")
# 添加图例
plt.legend()
# 显示绘图结果
plt.show()

此外还可以用多个矩阵评估指标评估模型性能：

 from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
# 计算均方误差（MSE）
mse = mean_squared_error(y_test, y_pred)
# 计算均方根误差（RMSE）
rmse = mean_squared_error(y_test, y_pred, squared=False)
# 计算决定系数（R^2）
r2 = r2_score(y_test, y_pred)
# 计算平均绝对误差（MAE）
mae = mean_absolute_error(y_test, y_pred)

# 打印评估结果
print("Mean Squared Error (MSE):", mse)
print("Root Mean Squared Error (RMSE):", rmse)
print("R-squared (R^2):", r2)
print("Mean Absolute Error (MAE):", mae)

## 结果
# Mean Squared Error (MSE): 138264386141.42395
# Root Mean Squared Error (RMSE): 371839.1939285367
# R-squared (R^2): 0.3787461308826928
# Mean Absolute Error (MAE): 143605.94681857855

4.讨论

岭回归是一种基于正则化的线性回归技术，通过引入L2范数惩罚项来平衡模型的拟合能力和复杂度。它在处理多重共线性和高维数据时具有显著优势，可以提高模型的稳定性和泛化能力。岭回归通过约束系数的大小，减小了变量间的相关性对模型预测的影响，避免了过拟合的问题。通过调节正则化参数alpha，可以控制岭回归模型的收缩程度，从而平衡模型的偏差和方差。

岭回归和Lasso回归在某种程度上是互补的，它们各自在特征选择和系数缩小方面有不同的优势。因此，根据具体问题的特点和数据集的情况，选择使用岭回归或Lasso回归，或者结合两者的方法，可以更好地处理线性回归问题，并获得更准确和稳定的模型。