0. 简介
融合方案是多传感器融合方法的关键,多传感器融合方法是地下矿山和行星表面等复杂极端环境下状态估计的最有前途的解决方案。本文提出了一种基于iEKF的轻量级LiDAR惯性里程计系统,该系统采用可感知退化的模块化传感器融合管道,仅在检测到退化时才在更新过程中同时测量来自另一个里程计的LiDAR点和相对位姿。通过CRLB理论和仿真实验验证了该方法与单一观测值方法相比具有更高的精度。此外,针对各种最先进的传感器融合方法,在感知挑战数据集上对所提出的系统进行了评估。结果表明,即使在恶劣的环境和较差的观测条件下,该系统仍具有较高的估计精度和实时性能。
虽然这个工作还没有开源,但是预计应该会在接收后开源吧,具体原文内容可以参考这里《DAMS-LIO: A Degeneration-Aware and Modular Sensor-Fusion LiDAR-inertial Odometry》。
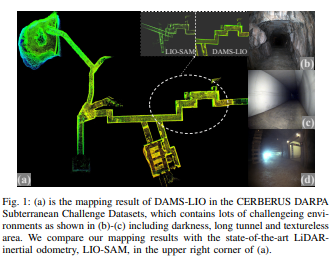
图1:(a)是DAMS-LIO在CERBERUS DARPA地下挑战数据集中的映射结果,其中包含许多具有挑战性的环境,如(b)-(c)所示,包括黑暗、长隧道和无纹理区域。我们将我们的映射结果与最先进的激光惯性测距导航系统LIO-SAM在(a)右上角进行比较。
1. 文章贡献
-
提出了一种基于退化感知和模块化传感器融合的轻量级激光雷达-惯性测程系统(DAMS-LIO),该系统能够在极端环境下进行鲁棒和准确的状态估计,在计算资源有限的情况下,为机器人执行复杂探测任务提供了明显的优势。
-
提出了一种新的传感器融合方法,将激光雷达和其他里程计的信息完全融合,仅在检测到退化时,将激光雷达点和其他里程计的相对位姿作为更新过程中的测量值。
-
基于CRLB定理进行了理论分析,以量化性能,并证明了所提出的传感器融合方法的高精度。
-
在模拟和真实数据集上的大量实验验证了我们方法的鲁棒性和准确性。
2. 系统架构
我们系统中每个坐标系的定义如图2所示。遵循典型的LIO坐标系定义,
{
L
}
\{L\}
{L}和
{
I
}
\{I\}
{I}分别对应于激光雷达和IMU坐标系,而
{
G
}
\{G\}
{G}是一个本地垂直参考坐标系,其原点与初始IMU位置重合。
{
O
}
\{O\}
{O}表示其他里程计测量,其原点标记为
{
M
}
\{M\}
{M}。
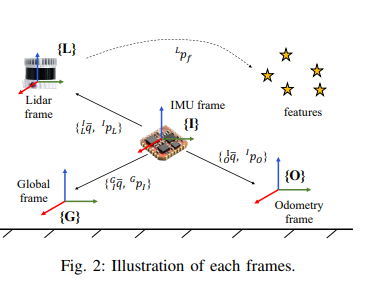
L p ^Lp Lp表示每个点相对于激光雷达坐标系的位置。一些重要且常用符号的定义在表格I中给出。

A. 状态向量(这部分内容比较通用)
我们系统中估计的状态包括当前的IMU状态 x I x_I xI,LiDAR和IMU之间的外参 I x L I_{x_L} IxL以及从其他里程计帧到IMU帧的变换 I x O I_{x_O} IxO。在时刻 t k t_k tk,状态可写为:
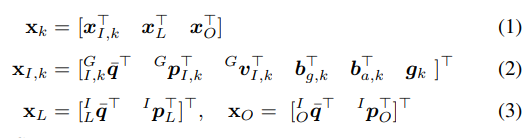
G
v
I
^Gv_I
GvI是IMU在全局坐标系下的速度,
b
g
,
k
b_{g,k}
bg,k和
b
a
,
k
b_{a,k}
ba,k分别表示陀螺仪和加速度计的偏差,
g
g
g是在
{
G
}
\{G\}
{G}坐标系下的重力向量,
x
L
=
{
L
I
q
ˉ
,
I
p
L
}
x_L = \{^I_L \bar{q}, ^Ip_L\}
xL={LIqˉ,IpL}和
x
O
=
{
O
I
q
ˉ
,
I
p
O
}
x_O = \{^I_O \bar{q}, ^Ip_O\}
xO={OIqˉ,IpO}表示从其他里程计坐标系{O}和LiDAR坐标系
{
L
}
\{L\}
{L}到IMU坐标系
{
I
}
\{I\}
{I}的变换。
B. IMU传播(同理IMU的传播)
由于IMU的测量受到偏差
b
b
b和零均值高斯噪声
n
n
n [15]的影响,因此它们可以被建模为:
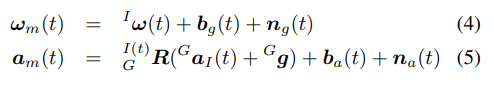
其中,
ω
m
(
t
)
ω_m(t)
ωm(t)和
a
m
(
t
)
a_m(t)
am(t)是原始的IMU测量数据,
I
ω
(
t
)
I_ω(t)
Iω(t)是IMU在本地坐标系
{
I
}
\{I\}
{I}下的角速度,
G
g
G_g
Gg和
G
a
I
(
t
)
G_{a_I}(t)
GaI(t)是重力和IMU在全局坐标系下的加速度。IMU运动学与[16]相同,为了保持简洁,我们这里不再重复描述。为了将协方差矩阵从时间
t
k
t_k
tk传递到时间
t
k
+
1
t_{k+1}
tk+1,我们按照[17]的线性离散时间模型生成格式:
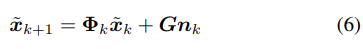
这段文本是关于状态向量和IMU传播的内容。其中,在
Φ
k
Φ_k
Φk是线性化的系统状态转移矩阵,
n
k
=
[
n
g
n
w
g
n
a
n
w
a
]
n_k=[n_g n_{wg} n_a n_{wa}]
nk=[ngnwgnanwa]是系统噪声。除了四元数以外,误差状态定义为
x
~
=
x
−
x
^
\tilde{x} = x − \hat{x}
x~=x−x^。其中,四元数通过关系式
q
=
q
^
⊗
δ
q
q = \hat{q}⊗δq
q=q^⊗δq定义。与[16]相同,符号
⊗
⊗
⊗表示四元数乘法,误差四元数定义为
δ
q
⋍
[
1
2
δ
θ
T
1
]
T
δq \backsimeq [ \frac{1}{2} δθ^T 1]^T
δq⋍[21δθT1]T。
如果将
n
k
n_k
nk的协方差定义为
Q
k
Q_k
Qk,则可以将状态协方差从
t
k
t_k
tk传播到
t
k
+
1
t_{k+1}
tk+1,具体方法见公式。
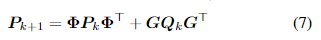
其中,
Φ
=
d
i
a
g
(
Φ
I
,
Φ
O
)
Φ = diag(Φ_I, Φ_O)
Φ=diag(ΦI,ΦO),
G
=
[
G
I
T
,
G
O
T
]
T
G = [G^T_I, G^T_O]^T
G=[GIT,GOT]T,
Φ
I
Φ_I
ΦI和
G
I
G_I
GI表示与其他里程计和IMU之间的外参之外的变量相关的部分,这与[12]中的定义相同。此外,
Φ
O
=
I
6
×
6
,
G
O
=
0
6
×
12
Φ_O = I_{6×6},G_O = 0_{6×12}
ΦO=I6×6,GO=06×12。
C. 测量模型(比较重点的知识)
1)LiDAR测量:对于来自LiDAR的测量,我们将其建模为[12]中的模型。在对在τi时间采样的扫描进行运动补偿后,我们将局部LiDAR坐标系中的第
j
j
j个点定义为
L
p
j
^Lp_j
Lpj。通过向后传播,该点可以更改为与
t
k
t_k
tk处IMU测量对应的扫描结束测量。同时,由于每个点应该位于地图中的小平面区域上,我们可以得到
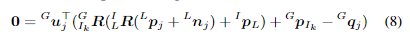
其中,
G
q
j
^Gq_j
Gqj 是小平面上的点,
G
u
j
^Gu_j
Guj 是平面的法向量。
I
R
L
^IR_L
IRL 和
G
R
I
k
^GR_{Ik}
GRIk 是对应于
%ILq
和
G
I
K
q
^GI_{Kq}
GIKq的旋转矩阵。
L
n
j
^Ln_j
Lnj 是点
L
p
j
^Lp_j
Lpj的测距和指向噪声。(8)也可以用更简洁的形式总结为:
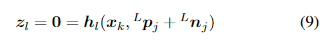
为了线性化更新的测量模型,我们将测量模型在
x
^
k
\hat{x}_k
x^k处进行一阶近似。
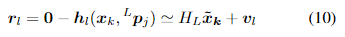 其中
v
l
∈
N
(
0
,
R
l
)
v_l ∈ N(0,R_l)
vl∈N(0,Rl)是由于原始测量噪声
L
n
j
^Ln_j
Lnj而产生的高斯噪声。
H
L
H_L
HL是残差
r
l
r_l
rl对误差状态
x
~
k
\tilde{x}_k
x~k的雅可比矩阵,给出如下:
其中
v
l
∈
N
(
0
,
R
l
)
v_l ∈ N(0,R_l)
vl∈N(0,Rl)是由于原始测量噪声
L
n
j
^Ln_j
Lnj而产生的高斯噪声。
H
L
H_L
HL是残差
r
l
r_l
rl对误差状态
x
~
k
\tilde{x}_k
x~k的雅可比矩阵,给出如下:
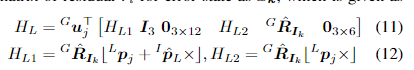
2) 另一种里程表测量:由于每个里程表的发布频率不同,我们执行线性插值以获取估计状态在时间
t
k
t_k
tk 和
t
k
+
1
t_{k+1}
tk+1 时的其他里程表姿态,并将它们的坐标系表示为
O
k
−
1
O_{k−1}
Ok−1 和
O
k
O_k
Ok。我们将从 A 到 B 的变换矩阵
A
T
B
^AT_B
ATB 定义为
A
T
B
=
[
A
R
B
,
A
p
B
;
0
3
×
3
,
1
]
^AT_B = [^AR_B ,^Ap_B ; 0_{3×3}, 1]
ATB=[ARB,ApB;03×3,1]。然后根据图 2,我们有以下变换关系:
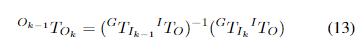
其中,$^{Q{k-1}}T_{O_k} = KaTeX parse error: Double superscript at position 19: …^{-1}_{O_{k-1}}^̲GT_{O_k} 是通过其他里程计计算出的相对位姿测量。因此,基于(13),我们可以很容易地得到测量模型
z
O
=
[
z
r
z
p
]
z_O = [\begin{matrix}z_r \\ z_p\end{matrix}]
zO=[zrzp],其中:
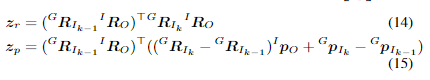
根据公式(10)计算的旋转和平移误差,其中
v
r
∈
N
(
0
,
R
r
)
v_r∈N(0,R_r)
vr∈N(0,Rr)和
v
p
∈
N
(
0
,
R
p
)
v_p∈N(0,R_p)
vp∈N(0,Rp)是相应的高斯噪声。因此,根据公式(14)和(15),我们可以得到旋转和平移残差的误差状态的雅可比矩阵。
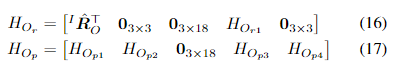
其中:
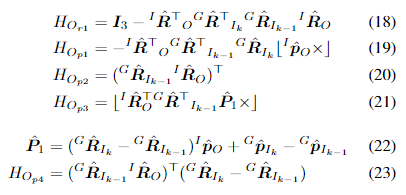
D. 变形感知更新(比较重点的知识)
与[12]类似,我们有以下误差状态:
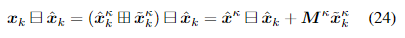
⊞
/
⊟
\boxplus/\boxminus
⊞/⊟表示Lie群中的加减运算符[18]。
M
κ
M_\kappa
Mκ是
(
x
^
k
κ
⊞
x
~
k
κ
)
⊟
x
^
k
(\hat{x}^\kappa_k \boxplus \tilde{x}^\kappa_k)\boxminus \hat{x}_k
(x^kκ⊞x~kκ)⊟x^k相对于
x
~
k
κ
\tilde{x}^\kappa_k
x~kκ的偏导数,以零为值进行评估。