简介

本例子函数参考了【1】中的函数，增加了解析方法的函数与四阶龙格-库塔方法对比，并计算了百分比误差，最大误差在0.3%左右。

参考

【1】Matlab代码分享-龙格库塔（Runge-Kutta）法

code

四阶龙格-库塔函数

参考自【1】链接

function [t,y]=Runge_Kutta4(fun,tb,te,y0,N,varargin)

%四阶龙格-库塔方法求解一阶微分方程数值解

%fun 微分方程

%tb t的取值范围的左端点

%te t的取值范围的左端点

%y0 y的迭代初始值

%N 步长

%如果函数的输入参数没有N时，步长数N取默认值200

if nargin<4

N = 200;

end

h = (te-tb)/N;%步长

t = tb+(0:N)'*h;

y = zeros(size(t));

y(1) = y0;

for k=1:N

K1 = feval(fun,t(k),y(k));

K2 = feval(fun,t(k)+h/2,y(k)+h/2*K1);

K3 = feval(fun,t(k)+h/2,y(k)+h/2*K2);

K4 = feval(fun,t(k),y(k)+h*K3);

y(k+1) = y(k) + h/6*(K1+2*K2+2*K3+K4);

end

end

微分方程函数

function f=RK4_fun(t,y)
f=-y+t.^2+3;
end

主程序

clc,clear,close all

%四阶龙格-库塔方法求解一阶微分方程数值解
tb=0;
te=3;
y0=1;
[t,soly]=Runge_Kutta4('RK4_fun',tb,te,y0,100);
disp([t,soly])
%解析法结果对比
tb=0;
te=3;
N=100;
h1=(te-tb)/N;
t1=tb+(0:N)'*h1;
ytrue=-4*exp(-t1)+t1.^2-2*t1+5;%解析法算的解
subplot(2,1,1);
plot(t,soly,'+',t1,ytrue,'*');

y_err=abs(soly-ytrue)./ytrue;
subplot(2,1,2);

plot(t,y_err,'*');
title('误差曲线');

结果

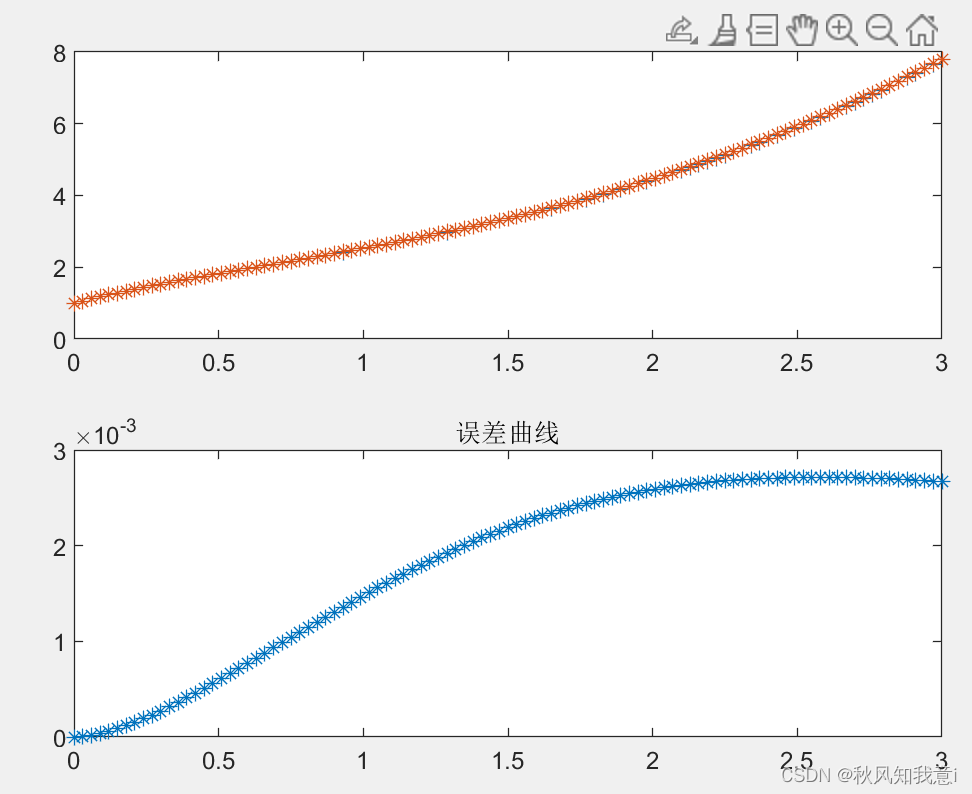
分析

从结果图中我们可以看到，绝对值误差在整个区间逐渐增大，最大有0.3%的误差，还是有相当的精度。