题目来源：https://leetcode.cn/problems/gas-station/description/

 

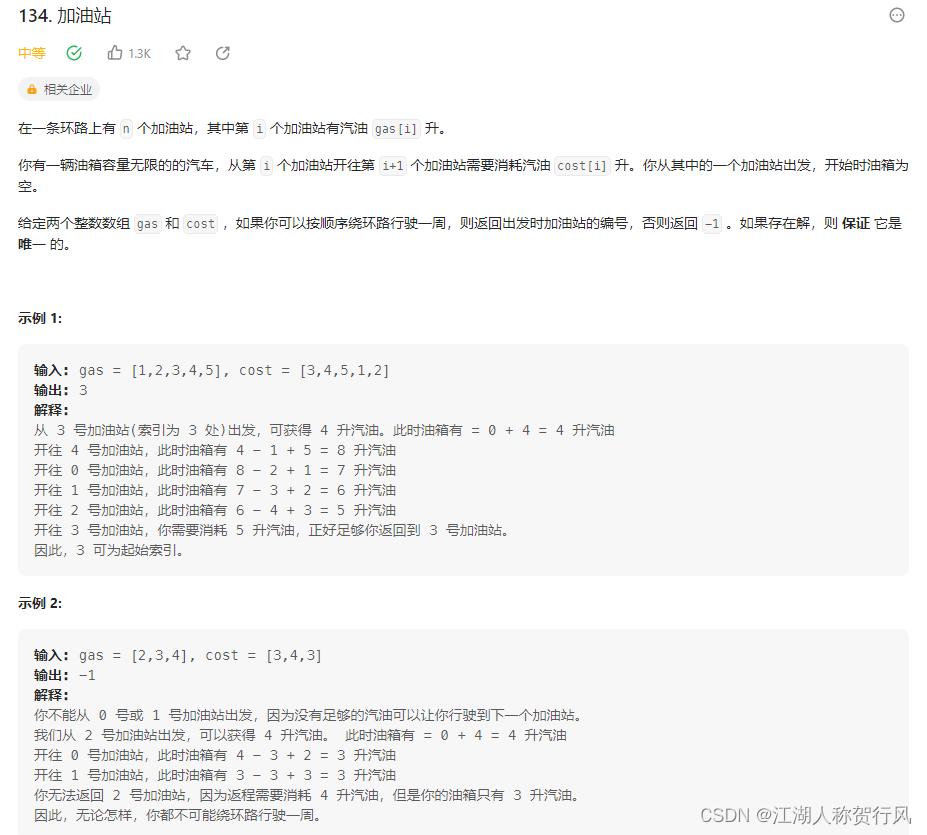
C++题解1： 感觉也属于暴力，有一点点简化。在汽油获得总量小于消耗总量时直接返回-1，对于出发的加油站编号，其当前站的汽油净获得量一定大于等于0，前一站的汽油净获得量一定小于0。

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int len = gas.size();
        vector<int> need(len, 0), inds;
        int sum = 0;
        for(int i = 0; i < len; i++) {
            need[i] = gas[i] - cost[i]; // 汽油净获得量
            sum = sum + need[i];
            // 保存可能的出发站
            if(i == 0 && need[i] >= 0) inds.push_back(0);
            else if(i > 0 && need[i] >= 0 && need[i-1] < 0) inds.push_back(i);
        }
        if(sum < 0) return -1;  // 总量判断
        // 遍历可能的出发站
        for(int j = 0 ; j < need.size(); j++){
            int acu = 0, k = inds[j];
            while(acu >= 0) { // 出现到不了的地方则跳出循环，去下一个可能的出发站
                acu = acu + need[k];
                k++;
                k = k%len;
                if(k == inds[j]) break; 
            }
            if(k == inds[j]) return inds[j];
        }
        return -1;
    }
};

C++题解2（来源代码随想录）：暴力解法

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        for (int i = 0; i < cost.size(); i++) {
            int rest = gas[i] - cost[i]; // 记录剩余油量
            int index = (i + 1) % cost.size();
            while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈（如果有rest==0，那么答案就不唯一了）
                rest += gas[index] - cost[index];
                index = (index + 1) % cost.size();
            }
            // 如果以i为起点跑一圈，剩余油量>=0，返回该起始位置
            if (rest >= 0 && index == i) return i;
        }
        return -1;
    }
};

C++题解3（来源代码随想录）：全局贪心。

• 情况一：如果gas的总和小于cost总和，那么无论从哪里出发，一定是跑不了一圈的

• 情况二：rest[i] = gas[i]-cost[i]为一天剩下的油，i从0开始计算累加到最后一站，如果累加没有出现负数，说明从0出发，油就没有断过，那么0就是起点。

• 情况三：如果累加的最小值是负数，汽车就要从非0节点出发，从后向前，看哪个节点能把这个负数填平，能把这个负数填平的节点就是出发节点。

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int min = INT_MAX; // 从起点出发，油箱里的油量最小值
        for (int i = 0; i < gas.size(); i++) {
            int rest = gas[i] - cost[i];
            curSum += rest;
            if (curSum < min) {
                min = curSum;
            }
        }
        if (curSum < 0) return -1;  // 情况1
        if (min >= 0) return 0;     // 情况2
                                    // 情况3
        for (int i = gas.size() - 1; i >= 0; i--) {
            int rest = gas[i] - cost[i];
            min += rest;
            if (min >= 0) {
                return i;
            }
        }
        return -1;
    }
};

C++题解4（来源代码随想录）：局部贪心。i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，因为这个区间选择任何一个位置作为起点，到i这里都会断油，那么起始位置从i+1算起，再从0计算curSum。

局部最优：当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i之前开始一定不行。全局最优：找到可以跑一圈的起始位置。局部最优可推出全局最优。

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int totalSum = 0;
        int start = 0;
        for (int i = 0; i < gas.size(); i++) {
            curSum += gas[i] - cost[i];
            totalSum += gas[i] - cost[i];
            if (curSum < 0) {   // 当前累加rest[i]和 curSum一旦小于0
                start = i + 1;  // 起始位置更新为i+1
                curSum = 0;     // curSum从0开始
            }
        }
        if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了
        return start;
    }
};