第一题:数位之和
给定一个十进制整数 n,输出 n 的各位数字之和。
输入格式
输入一个整数 n。
输出格式
输出一个整数,表示答案。
数据范围
1≤n≤1e9
输入样例:
20151220输出样例:
13样例解释
20151220 的各位数字之和为 2+0+1+5+1+2+2+0=13。
解题思路: 简单枚举每一位相加即可
以下是代码
C++
#include<iostream>
#include<algorithm>
using namespace std;
string s;
int main()
{
cin >> s;
int res = 0;
for(int i = 0;i < s.size();i ++)
res += s[i] - '0';
cout << res << endl;
return 0;
}Python
n = int(input())
res = 0
for i in str(n):
res += ord(i) - ord('0')
print(res)第二题:消除类游戏
消除类游戏是深受大众欢迎的一种游戏,游戏在一个包含有 n 行 m 列的游戏棋盘上进行,棋盘的每一行每一列的方格上放着一个有颜色的棋子,当一行或一列上有连续三个或更多的相同颜色的棋子时,这些棋子都被消除。
当有多处可以被消除时,这些地方的棋子将同时被消除。
现在给你一个 n 行 m 列的棋盘,棋盘中的每一个方格上有一个棋子,请给出经过一次消除后的棋盘。
请注意:一个棋子可能在某一行和某一列同时被消除。
输入格式
输入的第一行包含两个整数 n,m,用空格分隔,分别表示棋盘的行数和列数。
接下来 n 行,每行 m 个整数,用空格分隔,分别表示每一个方格中的棋子的颜色。
颜色使用 1 至 9 编号。
输出格式
输出 n 行,每行 m 个整数,相邻的整数之间使用一个空格分隔,表示经过一次消除后的棋盘。
如果一个方格中的棋子被消除,则对应的方格输出 0,否则输出棋子的颜色编号。
数据范围
所有的评测用例满足:1≤n,m≤30。
输入样例1:
4 5 2 2 3 1 2 3 4 5 1 4 2 3 2 1 3 2 2 2 4 4输出样例1:
2 2 3 0 2 3 4 5 0 4 2 3 2 0 3 0 0 0 4 4样例1解释
棋盘中第 4 列的 1 和第 4 行的 2 可以被消除,其他的方格中的棋子均保留。
输入样例2:
4 5 2 2 3 1 2 3 1 1 1 1 2 3 2 1 3 2 2 3 3 3输出样例2:
2 2 3 0 2 3 0 0 0 0 2 3 2 0 3 2 2 0 0 0样例2解释
棋盘中所有的 1 以及最后一行的 3 可以被同时消除,其他的方格中的棋子均保留。
解题思路:题目描述一行或一列上有连续三个或更多的棋子时,会被消除,因此我们可以遍历每一个点检查是否有连续三个相连,如果有那么,将这个点置成0即可
以下是代码
C++
#include<iostream>
#include<cstring>
using namespace std;
const int N = 50;
int n , m;
int g[N][N];
bool st[N][N];
int main()
{
memset(st , 0 , sizeof st);
cin >> n >> m;
for(int i = 0;i < n;i ++)
for(int j = 0;j < m;j ++)
cin >> g[i][j];
for(int i = 0;i < n;i ++)
for(int j = 0;j < m;j ++)
{
if(j + 2 < m && g[i][j] == g[i][j + 1] && g[i][j + 1] == g[i][j + 2])
st[i][j] = st[i][j + 1] = st[i][j + 2] = 1;
if(i + 2 < n && g[i][j] == g[i + 1][j] && g[i + 2][j] == g[i + 1][j])
st[i][j] = st[i + 1][j] = st[i + 2][j] = 1;
}
for(int i = 0;i < n;i ++)
{
for(int j = 0;j < m;j ++)
if(st[i][j]) cout << "0 ";
else cout << g[i][j] << " ";
cout << endl;
}
return 0;
}第三题:画图
用 ASCII 字符来画图是一件有趣的事情,并形成了一门被称为 ASCII Art 的艺术。
例如,下图是用 ASCII 字符画出来的 CSPRO 字样。
..____.____..____..____...___.. ./.___/.___||.._.\|.._.\./._.\. |.|...\___.\|.|_).|.|_).|.|.|.| |.|___.___).|..__/|.._.<|.|_|.| .\____|____/|_|...|_|.\_\\___/.本题要求编程实现一个用 ASCII 字符来画图的程序,支持以下两种操作:
- 画线:给出两个端点的坐标,画一条连接这两个端点的线段。简便起见题目保证要画的每条线段都是水平或者竖直的。水平线段用字符
-来画,竖直线段用字符|来画。如果一条水平线段和一条竖直线段在某个位置相交,则相交位置用字符+代替。- 填充:给出填充的起始位置坐标和需要填充的字符,从起始位置开始,用该字符填充相邻位置,直到遇到画布边缘或已经画好的线段。注意这里的相邻位置只需要考虑上下左右 4 个方向,如下图所示,字符
@只和 4 个字符*相邻。.*. *@* .*.输入格式
第 1 行有三个整数 m,n 和 q。m 和 n 分别表示画布的宽度和高度,以字符为单位。q 表示画图操作的个数。
第 2 行至第 q+1 行,每行是以下两种形式之一:
0 x1 y1 x2 y2:表示画线段的操作,(x1,y1) 和 (x2,y2) 分别是线段的两端,满足要么 x1=x2 且 y1≠y2,要么 y1=y2 且 x1≠x2。1 x y c:表示填充操作,(x,y) 是起始位置,保证不会落在任何已有的线段上;c 为填充字符,是大小写字母。画布的左下角是坐标为 (0,0) 的位置,向右为 x 坐标增大的方向,向上为 y 坐标增大的方向。
这 q 个操作按照数据给出的顺序依次执行。画布最初时所有位置都是字符
.(小数点)。输出格式
输出有 n 行,每行 m 个字符,表示依次执行这 q 个操作后得到的画图结果。
数据范围
2≤m,n≤100,
0≤q≤100,
0≤x<m(x 表示输入数据中所有位置的 x 坐标),
0≤y<n(y 表示输入数据中所有位置的 y 坐标)。输入样例1:
4 2 3 1 0 0 B 0 1 0 2 0 1 0 0 A输出样例1:
AAAA A--A输入样例2:
16 13 9 0 3 1 12 1 0 12 1 12 3 0 12 3 6 3 0 6 3 6 9 0 6 9 12 9 0 12 9 12 11 0 12 11 3 11 0 3 11 3 1 1 4 2 C输出样例2:
................ ...+--------+... ...|CCCCCCCC|... ...|CC+-----+... ...|CC|......... ...|CC|......... ...|CC|......... ...|CC|......... ...|CC|......... ...|CC+-----+... ...|CCCCCCCC|... ...+--------+... ................
解题思路:
对于填充操作,使用深度优先遍历进行图画
对于画线操作,直接遍历的方法进行遍历
坑点:注意这里的坐标和数组中使用的坐标是相反的,仅仅只需要倒着读入就行
以下是代码
C++
#include<iostream>
#include<cstring>
using namespace std;
const int N = 110;
int n , m , q;
char g[N][N];
bool st[N][N];
void dfs(int x , int y , char ch)
{
if(x < 0 || x >= n || y < 0 || y >= m) return ;
if(st[x][y] || g[x][y] == '-' || g[x][y] == '|' || g[x][y] == '+') return ;
st[x][y] = true;
g[x][y] = ch;
dfs(x + 1 , y , ch);
dfs(x - 1 , y , ch);
dfs(x , y + 1 , ch);
dfs(x , y - 1 , ch);
}
void change(int x1 , int y1 , int x2 , int y2)
{
if(x1 == x2)
{// 同一行
for(int i = y1;i <= y2;i ++)
{
if(g[x1][i] == '|' || g[x1][i] == '+') g[x1][i] = '+';
else g[x1][i] = '-';
}
}
// 同一列
else if (y1 == y2)
{
for(int i = x1;i <= x2;i ++)
{
if(g[i][y1] == '-' || g[i][y1] == '+') g[i][y1] = '+';
else g[i][y1] = '|';
}
}
}
int main()
{
cin >> m >> n >> q;
for(int i = 0;i < n;i ++)
for(int j = 0;j < m;j ++)
g[i][j] = '.';
while(q --)
{
// x 宽度
// y 高度
int type , x , y;
cin >> type;
// 填充操作
if(type)
{
memset(st , 0 , sizeof st);
char ch;
cin >> y >> x >> ch;
dfs(x , y , ch);
}
// 画线段的操作
else
{
int y1 , x1;
cin >> y >> x >> y1 >> x1;
if(x > x1) swap(x , x1);
if(y > y1) swap(y , y1);
change(x , y , x1 , y1);
}
}
for(int i = n - 1;i >= 0;i --)
{
for(int j = 0;j < m;j ++)
cout << g[i][j];
cout << endl;
}
return 0;
}第四题:送货
为了增加公司收入,F 公司新开设了物流业务。
由于 F 公司在业界的良好口碑,物流业务一开通即受到了消费者的欢迎,物流业务马上遍及了城市的每条街道。
然而,F 公司现在只安排了小明一个人负责所有街道的服务。
任务虽然繁重,但是小明有足够的信心,他拿到了城市的地图,准备研究最好的方案。
城市中有 n 个交叉路口,m 条街道连接在这些交叉路口之间,每条街道的首尾都正好连接着一个交叉路口。
除开街道的首尾端点,街道不会在其他位置与其他街道相交。
每个交叉路口都至少连接着一条街道,有的交叉路口可能只连接着一条或两条街道。
小明希望设计一个方案,从编号为 1 的交叉路口出发,每次必须沿街道去往街道另一端的路口,再从新的路口出发去往下一个路口,直到所有的街道都经过了正好一次。
输入格式
输入的第一行包含两个整数 n,m,表示交叉路口的数量和街道的数量,交叉路口从 1 到 n 标号。
接下来 m 行,每行两个整数 a,b(a≠b),表示和标号为 a 的交叉路口和标号为 b 的交叉路口之间有一条街道,街道是双向的,小明可以从任意一端走向另一端。
两个路口之间最多有一条街道。
输出格式
如果小明可以经过每条街道正好一次,则输出一行包含 m+1 个整数 p1,p2,p3,…,pm+1,表示小明经过的路口的顺序,相邻两个整数之间用一个空格分隔。
如果有多种方案满足条件,则输出字典序最小的一种方案,即首先保证 p1 最小,p1 最小的前提下再保证 p2 最小,依此类推。
如果不存在方案使得小明经过每条街道正好一次,则输出一个整数 −1。
数据范围
前 30%30% 的评测用例满足:1≤n≤10,n−1≤m≤20。
前 50%50% 的评测用例满足:1≤n≤100,n−1≤m≤10000。
所有评测用例满足:1≤n≤10000,n−1≤m≤100000。输入样例1:
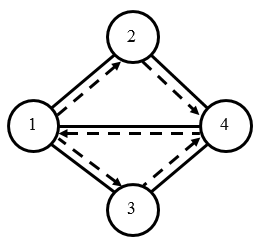
4 5 1 2 1 3 1 4 2 4 3 4输出样例1:
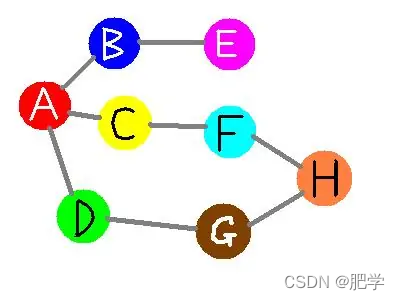
1 2 4 1 3 4样例1解释
城市的地图和小明的路径如下图所示。
输入样例2:
4 6 1 2 1 3 1 4 2 4 3 4 2 3输出样例2:
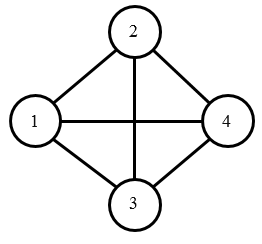
-1样例2解释
城市的地图如下图所示,不存在满足条件的路径。
解题思路:读题,可以知道需要找一条每一条边只经过一次的路径,这就是欧拉回路的经典模型。
存在欧拉回路的条件
1.每一个节点的度数是偶的
2.有且只有两个点的度数是奇的
对于这个题目:首先需要统计每一个节点的度数,注意题目并没有保证是联通的,因此需要使用并查集进行判断,注意题目需要从1号点出发,因此如果有度数为奇数的点,1号点一定是其中之一。
以下是代码
C++
// 使用并查集检查是否联通
// 使用欧拉回路判断条件进行判断是否有通路
// 使用dfs进行通路的枚举
#include<iostream>
#include<set>
using namespace std;
const int N = 10010 , M = 100010;
// 存边
set<int>se[M];
int res[M] , idx;
int p[M];
int n , m;
int find(int x)
{
if(x != p[x]) p[x] = find(p[x]);
return p[x];
}
void dfs(int u)
{
while(se[u].size())
{
int t = *se[u].begin();
se[u].erase(t) , se[t].erase(u);
dfs(t);
}
res[++ idx] = u;
}
int main()
{
cin >> n >> m;
for(int i = 1;i <= n;i ++)
p[i] = i;
while(m --)
{
int a , b;
cin >> a >> b;
se[a].insert(b) , se[b].insert(a);
if(find(a) != find(b)) p[find(a)] = find(b);
}
int cnt = 0;
for(int i = 1;i <= n;i ++)
{
if(find(i) != find(1))
{
puts("-1");
return 0;
}
// 计算奇数度数的点
else if(se[i].size() % 2) cnt ++;
}
// 题目需要从1号点出发因此1号点的度数应该是奇数
if(cnt != 2 && cnt != 0 || cnt == 2 && se[1].size() % 2 == 0)
{
puts("-1");
return 0;
}
dfs(1);
for(int i = idx;i;i --)
cout << res[i] << " ";
return 0;
}第五题:矩阵
题目很长,题目需要使用矩阵乘法、快速幂、位运算(考试的时候大概率做不出来)直接学习其他人的就行。
以下是代码
C++
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("inline")
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned int UI;
const int N = 1010, M = 32;
struct Bit
{
UI a[M];
void set1(int x)
{
a[x >> 5] |= 1u << (x & 31);
}
void set0(int x)
{
a[x >> 5] &= ~(1u << (x & 31));
}
int get(int x)
{
return a[x >> 5] >> (x & 31) & 1;
}
Bit operator& (const Bit& b) const
{
Bit c;
for (int i = 0; i < M; i ++ )
c.a[i] = a[i] & b.a[i];
return c;
}
int count_single(UI x)
{
x = x ^ (x >> 1);
x = x ^ (x >> 2);
x = x ^ (x >> 4);
x = x ^ (x >> 8);
x = x ^ (x >> 16);
return x;
}
int count()
{
int res = 0;
for (int i = 0; i < M; i ++ )
res ^= count_single(a[i]);
return res & 1;
}
};
struct Mat
{
Bit h[N], v[N];
int n, m;
Mat operator* (const Mat& b) const
{
Mat c;
c.n = n, c.m = b.m;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < b.m; j ++ )
if ((h[i] & b.v[j]).count())
c.h[i].set1(j), c.v[j].set1(i);
else
c.h[i].set0(j), c.v[j].set0(i);
return c;
}
}b, A[30];
char str[N];
int main()
{
int m;
scanf("%d", &m);
A[0].n = A[0].m = m, b.n = m, b.m = 1;
for (int i = 0; i < m; i ++ )
{
scanf("%s", str);
for (int j = 0; j < m; j ++ )
if (str[j] == '1')
A[0].h[i].set1(j), A[0].v[j].set1(i);
}
for (int i = 1; i < 30; i ++ ) A[i] = A[i - 1] * A[i - 1];
scanf("%s", str);
for (int i = 0; i < m; i ++ )
if (str[i] == '1')
b.h[i].set1(0), b.v[0].set1(i);
int n;
scanf("%d", &n);
while (n -- )
{
int k;
scanf("%d", &k);
Mat res = b;
for (int i = 0; i < 30; i ++ )
if (k >> i & 1)
res = A[i] * res;
for (int i = 0; i < m; i ++ )
printf("%d", res.h[i].get(0));
puts("");
}
return 0;
}