36、最长回文子串

(1) 题目解析

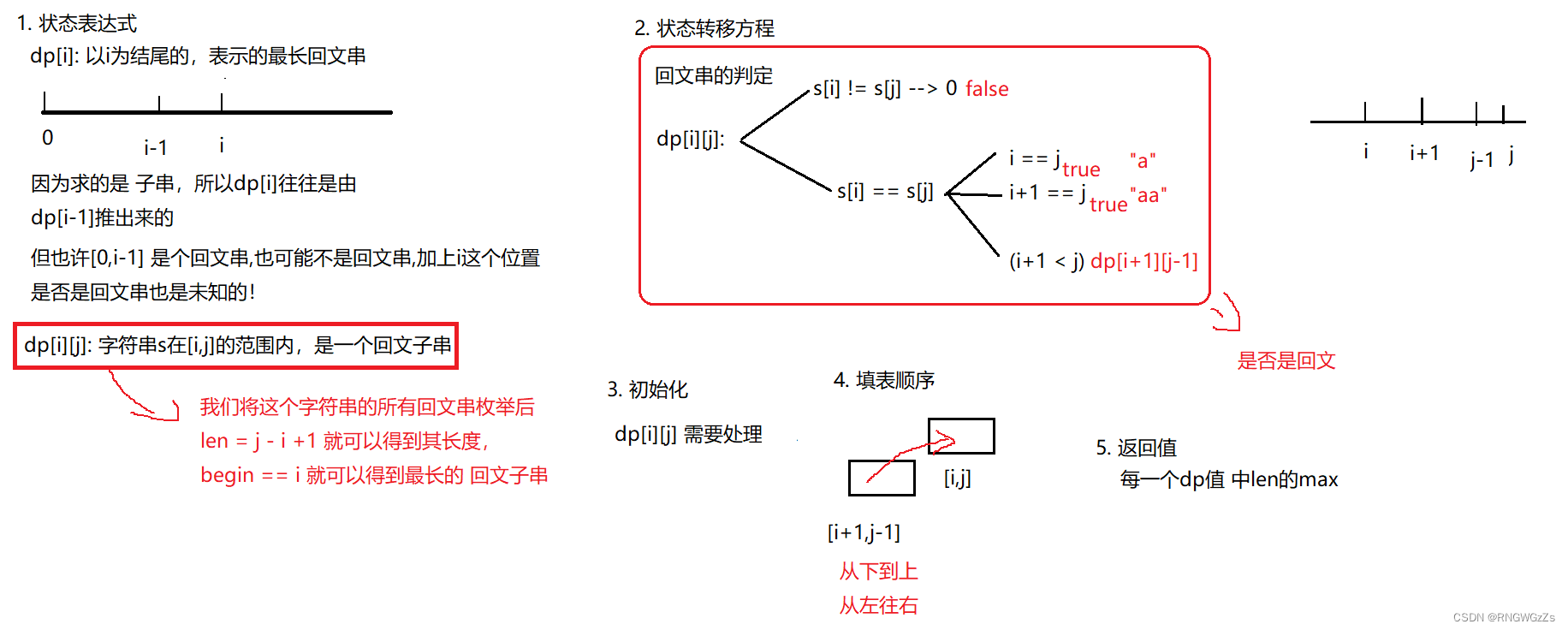
针对这一类回文串的动规问题得出该题解的状态表达式，不是经验+题目要求，以什么位置为结尾…… 因为，这样定义的状态表达式是得不出求不出转移方程的。

(2) 算法原理

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();

        vector<vector<bool>> dp(n,vector<bool>(n));

        int len = 0,begin = 0;
        for(int i=n-1; i>=0; --i) // 从上往下
        {
            // [i,j]
            for(int j=i; j<n;++j) // 从左往右
            {
                if(s[i] == s[j]) dp[i][j] = i+1 < j ? dp[i+1][j-1]:true;

                if(dp[i][j] && j-i+1 > len)
                {
                    // 判断
                    len = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substr(begin,len);
    }
};

37、回文串分割Ⅳ

(1) 题目解析

(2) 算法原理

class Solution {
public:
    bool checkPartitioning(string s) {
        int n = s.size();

        vector<vector<bool>> dp(n,vector<bool>(n));
        for(int i=n-1;i>=0;--i)
        {
            for(int j=i; j<n;++j)
            {
                if(s[i] == s[j]) dp[i][j] = i + 1 < j ? dp[i+1][j-1] : true;
            }
        } 

        // 枚举第二个字符串开头~留最后一个
        for(int i=1; i<n-1;++i)
        {
            // 枚举第三个字符串开头
            for(int j=i;j<n-1;++j)
            {
                if(dp[0][i-1] && dp[i][j] && dp[j+1][n-1])
                    return true;
            }
        }
        return false;
    }
};

38、回文串分割Ⅱ

(1) 题目解析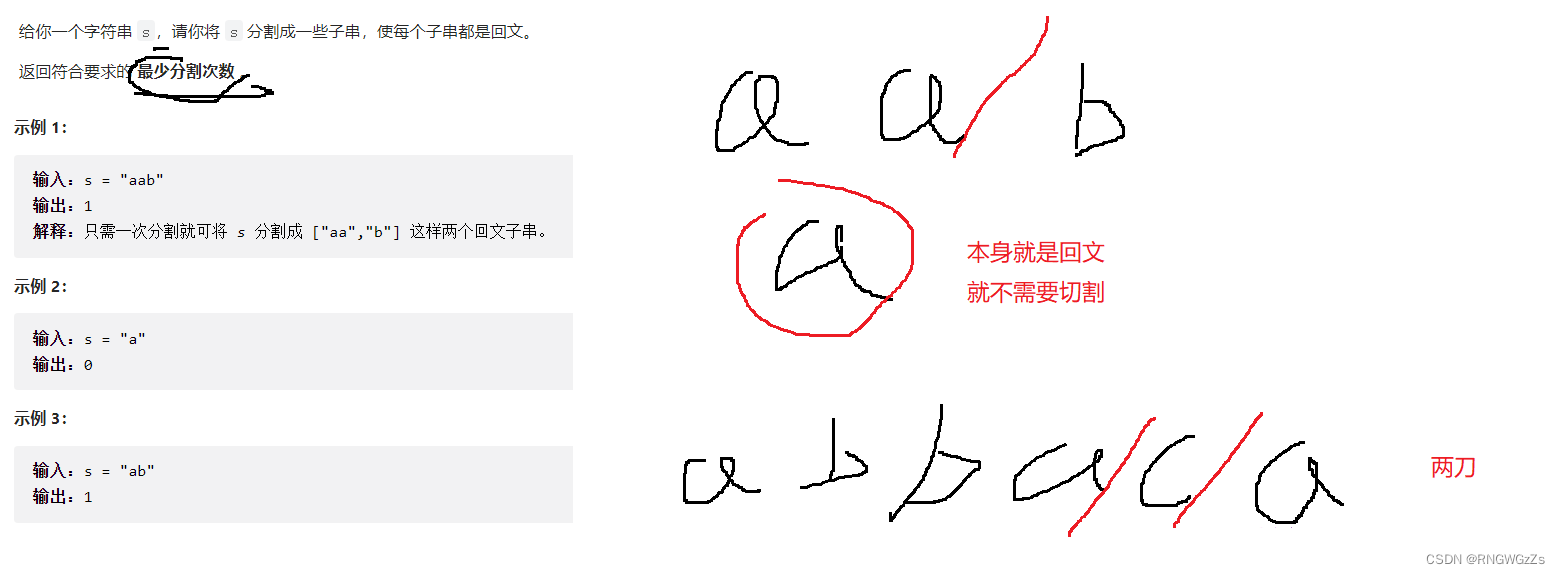

虽然这道题的要求是求最少的分割次数，但是和之前的回文串分割是大差不差的。

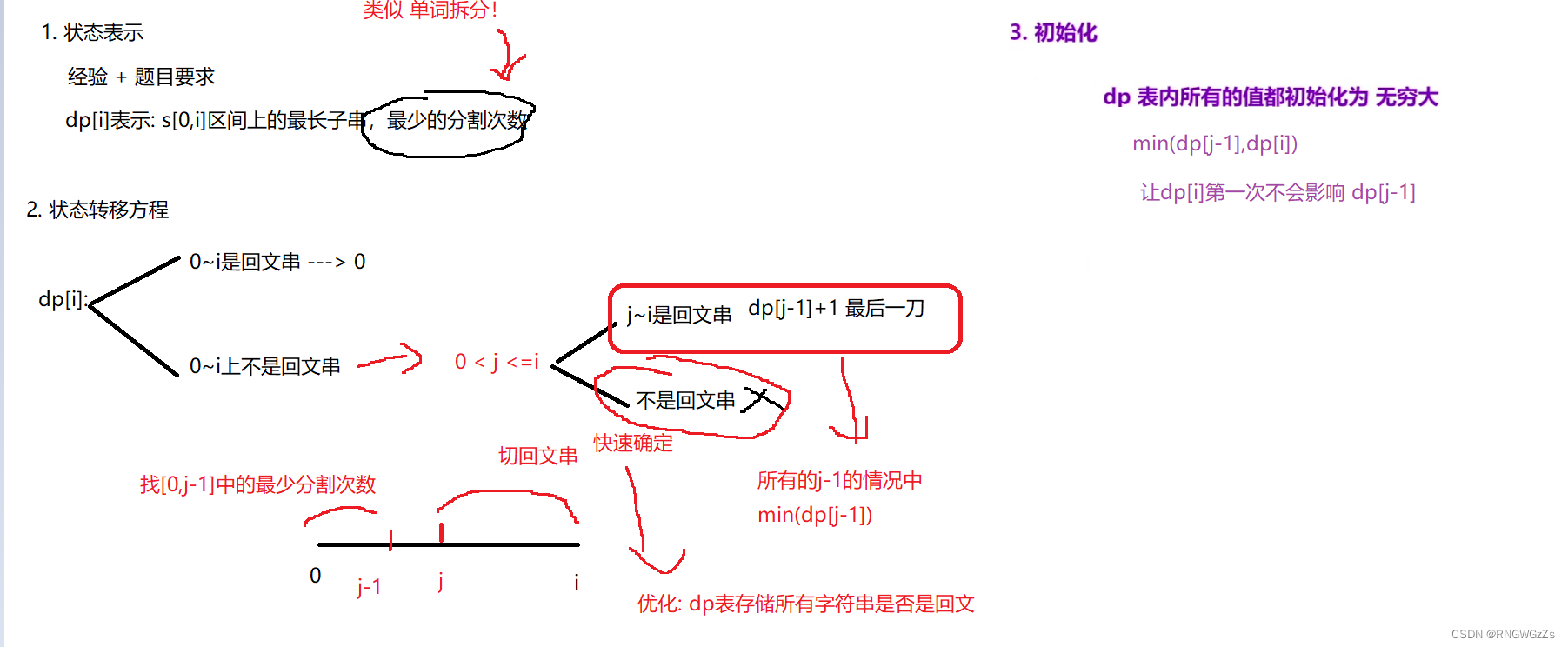
(2) 算法原理

class Solution {
public:
    int minCut(string s) {
        int n = s.size();

        vector<vector<bool>> isPal(n,vector<bool>(n));
        for(int i=n-1; i>=0;--i)
        {
            for(int j=i; j<n; ++j)
            {
                if(s[i] == s[j]) isPal[i][j] = i + 1 < j ? isPal[i+1][j-1]:true;
            }
        }

        // 处理分割次数
        // dp[i]: [0,i]的最少分割次数
        vector<int> dp(n,INT_MAX);
        for(int i=0; i<n;++i)
        {
            if(isPal[0][i]) dp[i] = 0;
            else 
            {
                // 不是回文 枚举0~i
                for(int j=1; j<=i;++j)
                {
                    // j~i是回文串
                    if(isPal[j][i]) dp[i] = min(dp[j-1]+1,dp[i]);
                }
            }
        }
        return dp[n-1];
    }
};

39、最长回文子序列

(1) 题目解析

(2) 算法原理

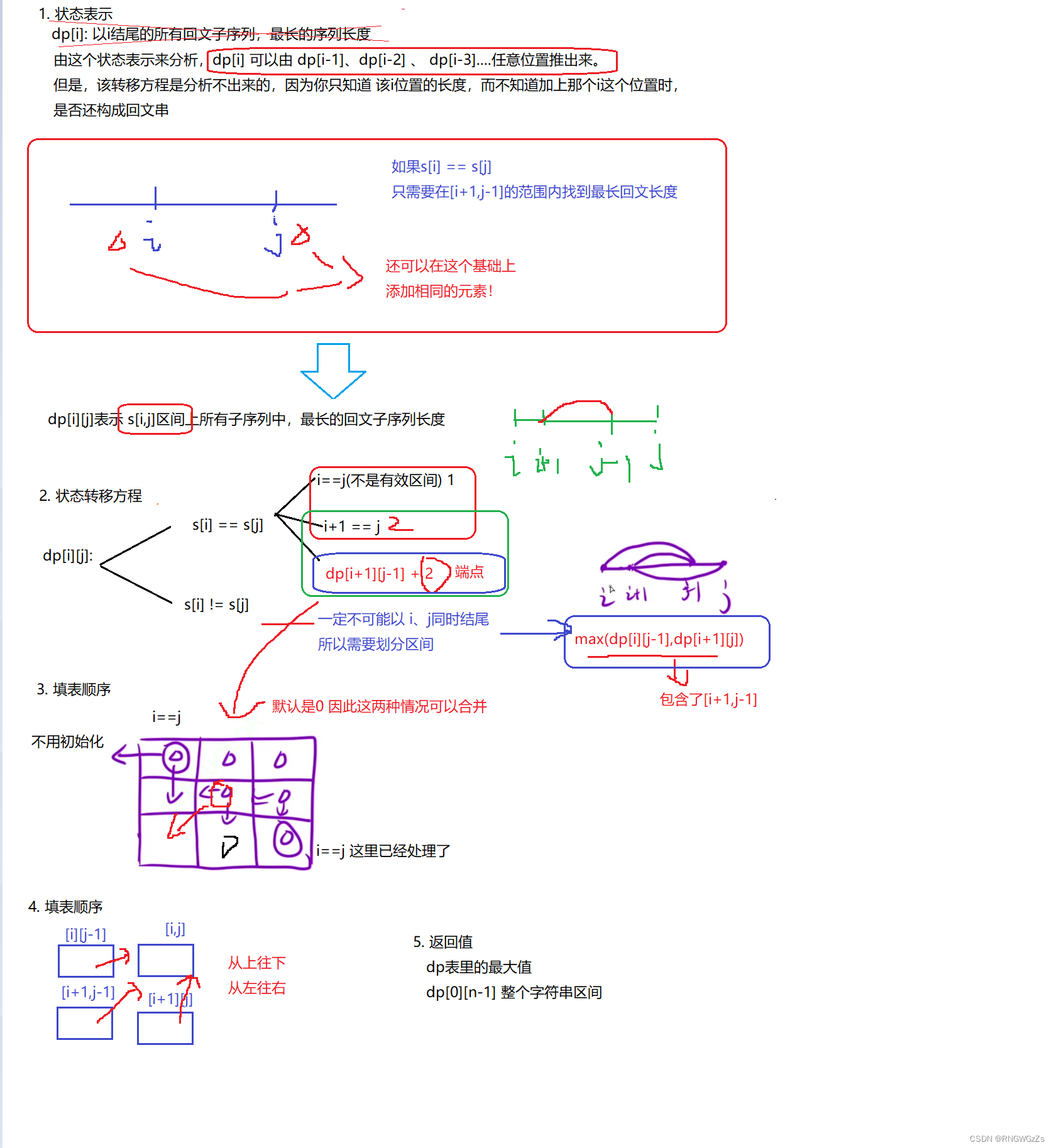
class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        // dp[i][j]: [i,j]区间里最长回文子序列
        vector<vector<int>> dp(n,vector<int>(n));
        for(int i=n-1; i>=0; --i)
        {
            // 因为j是从i位置起的 但是 i==j时 长度为1
            dp[i][i] = 1;
            for(int j=i+1;j<n;++j)
            {
                if(s[i] == s[j])
                    dp[i][j] = dp[i+1][j-1]+2;  
                else
                    dp[i][j] = max(dp[i][j-1],dp[i+1][j]);
            }
        }
        return dp[0][n-1];
    }
};

40、让字符串成为回文串的最小插入次数

(1) 题目解析

(2) 算法原理

class Solution {
public:
    int minInsertions(string s) {
        int n = s.size();
        vector<vector<int>> dp(n,vector<int>(n));
        for(int i=n-1;i>=0;--i)
        {
            // 因为 i==j 直接为0 这个位置不用考虑
            for(int j=i+1;j<n;++j)
            {
                if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1];
                else dp[i][j] = min(dp[i][j-1],dp[i+1][j]) + 1;
            }
        }
        return dp[0][n-1];
    }
};

本篇到此结束，感谢你的阅读。

祝你好运，向阳而生~