本文来自公众号“AI大道理”

 ——————

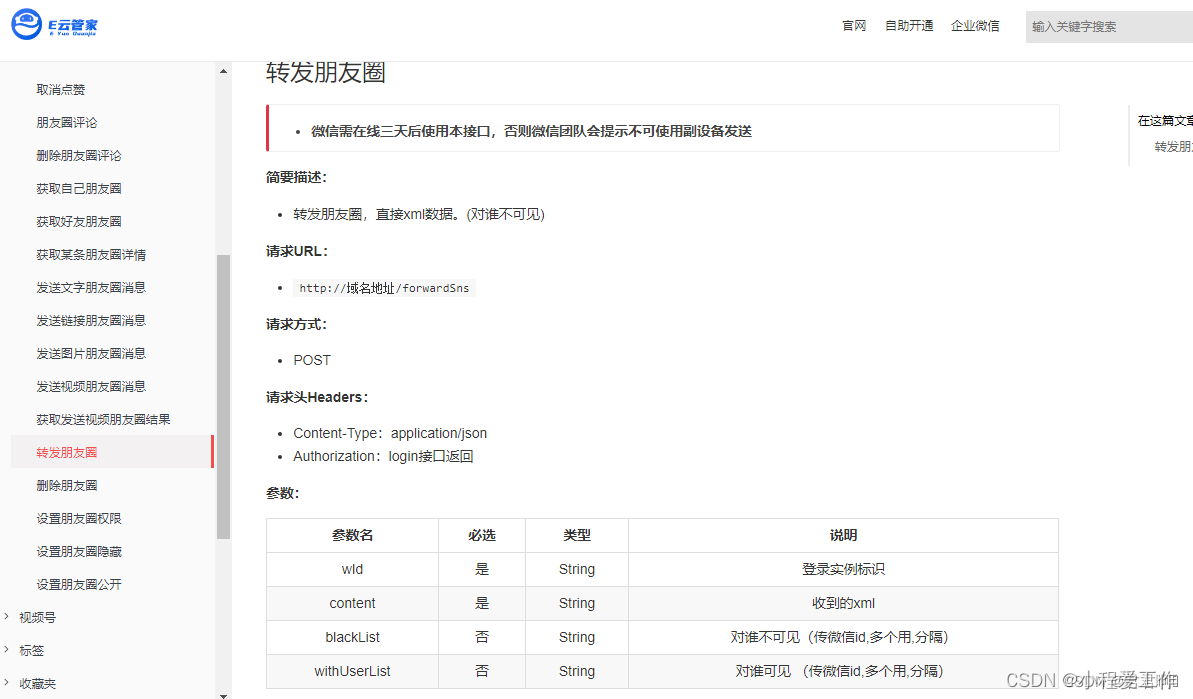
目标跟踪中，在数据关联后往往要进行卡尔曼滤波。

数据关联算法得到了每个目标的观测数据。

卡尔曼滤波使用关联的观测数据来估计目标的状态，并预测目标的未来位置和速度等信息。

目标跟踪过程中，测量数据通常会受到各种噪声的影响，例如传感器噪声、环境干扰等。卡尔曼滤波器可以通过对测量数据和系统模型的加权处理来减少噪声的影响，提供更准确的目标状态估计。

 

1、卡尔曼滤波简介

卡尔曼滤波用来估计带噪信号中隐藏的真实信息。

卡尔曼滤波是一种利用线性状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。

由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。

卡尔曼滤波利用目标的动态信息，设法去掉噪声的影响，得到一个关于目标位置的估计。这个估计可以是对当前目标位置的估计（滤波），也可以是对将来位置的估计（预测），也可以是对过去位置的估计（插值或平滑）。

卡尔曼滤波本质上是一个数据融合算法，将具有同样测量目的、来自不同传感器、(可能) 具有不同单位 (unit) 的数据融合在一起，得到一个更精确的目的测量值。

卡尔曼滤波基于状态空间模型，将系统的状态建模为一个随时间变化的状态向量，同时考虑了系统的测量值和系统动态之间的关系。它利用贝叶斯推断的思想，在每个时刻通过融合系统的观测值和先验预测，来估计系统的当前状态。

卡尔曼滤波主要包括两个步骤：预测步骤和更新步骤。

• 预测步骤（Prediction）：根据系统的动态模型，使用上一时刻的状态估计和控制输入，预测系统的下一时刻状态和状态协方差。

• 更新步骤（Update）：通过比较系统的观测值和预测值，结合观测噪声和系统模型的不确定性，更新系统的状态估计和协方差。

卡尔曼滤波通过递归的方式进行状态估计，每个时刻的状态估计都会考虑前一时刻的估计结果和当前的观测值。

需要注意的是，卡尔曼滤波的有效性和准确性取决于系统模型和噪声模型的准确性。如果系统模型或噪声模型与实际情况不符，卡尔曼滤波可能会产生较大的估计误差。因此，在应用卡尔曼滤波时，需要合理选择模型并进行参数调整和验证，以确保其适用性和效果。

2、卡尔曼滤波适用系统

卡尔曼滤波适用于线性高斯系统。

线性系统满足叠加性和齐次性，高斯指的噪声满足正态分布。

滤波即加权，理想状态下真实信号权重为1，噪声权重为0。

实际情况下则不是1和0，可能是0.7，0.3等。

卡尔曼滤波就是权重可选可调整的滤波，融合估计值的权重和观测值的权重得到一个修正的值。

估计的预测值不一定准，观测的（传感器的测量值、yolov5目标检测值）也不一定准，所以两者融合一下就可能得到更准确的值。

这里权重给的多少就看你更信任哪里值了。

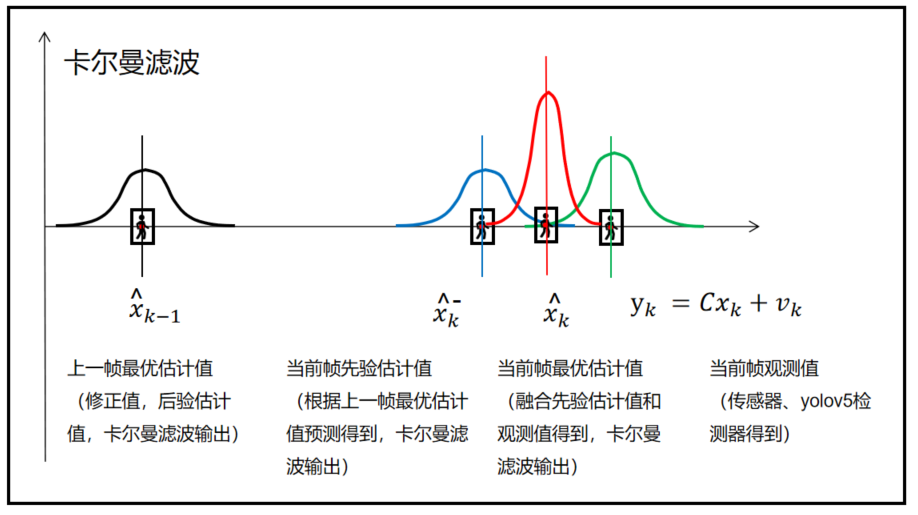
卡尔曼滤波这个算法的作用，就是在既有“过程误差”，又有“观测误差”的真实世界里，寻找一个最优的估计。

如何从两个概率分布中找到最准确的那个估计值呢？

卡尔曼滤波直接将两个概率分布相乘！

3、卡尔曼滤波基础：状态空间表达式

因为卡尔曼滤波是基于状态方程展开讨论的，所以在介绍卡尔曼滤波器之前需要建立一个状态空间方程组。

状态空间表达式是描述系统动态行为的一种数学形式，常用于卡尔曼滤波和系统控制理论中。

它将系统的状态、输入和输出之间的关系表示为一组差分方程或微分方程。

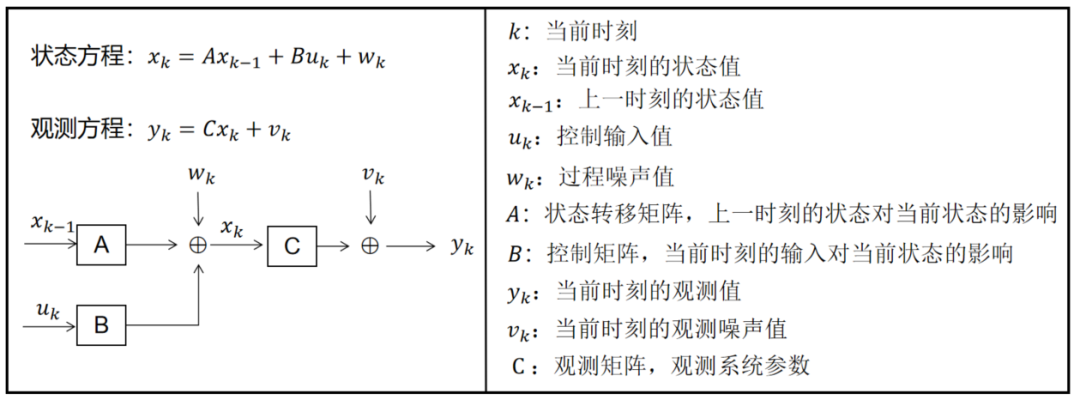
状态方程描述了系统的状态如何随时间演变。

观测方程则表示了状态与观测输出之间的关系。

通过状态方程和观测方程，可以进行状态估计、滤波、预测和控制等操作。

4、卡尔曼滤波基础：高斯分布（正态分布）

正态分布（Normal Distribution），也称常态分布，又名高斯分布（Gaussian Distribution），是一个常见的连续概率分布。

一维高斯分布：

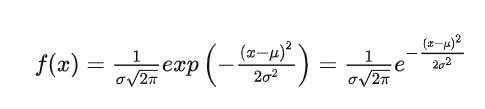
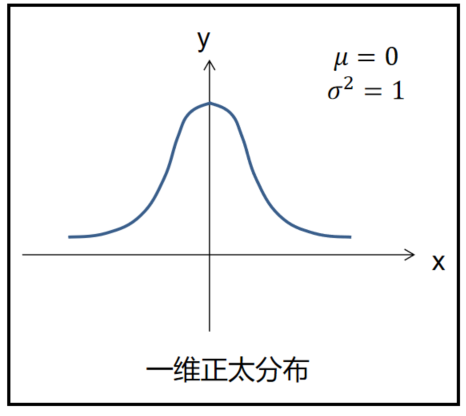
高斯分布的形状是一个钟形曲线，其峰值位于均值处。标准差决定了曲线的宽度，标准差越大，曲线越宽，表示观测值的变异程度越大。

多维高斯分布：

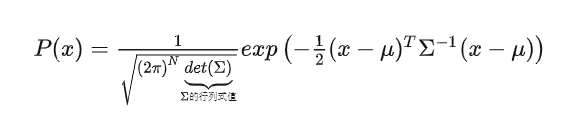
高斯分布融合：

A,B为相互独立的条件：即事件A（或B）是否发生对事件B（A）发生的概率没有影响。那么，AB 同时发生P(AB)=P(A)P(B)。

假如A,B都服从高斯分布：

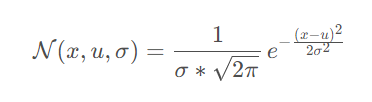
有高斯分布1：

有高斯分布2：

对分布进行融合：

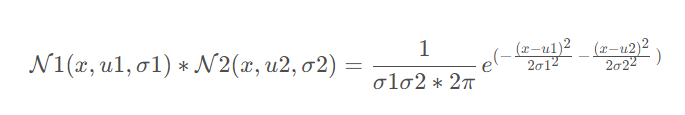
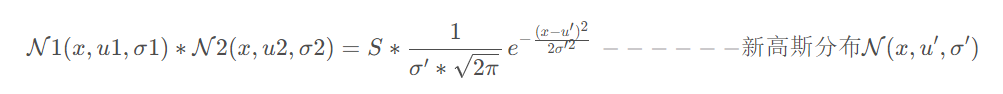
两个高斯分布相乘依旧是高斯分布。

5、卡尔曼滤波公式推导

卡尔曼滤波使用上一次的最优结果预测当前值，使用观测结果修正当前预测值，得到当前最优结果。

先验估计：

先验估计协方差：

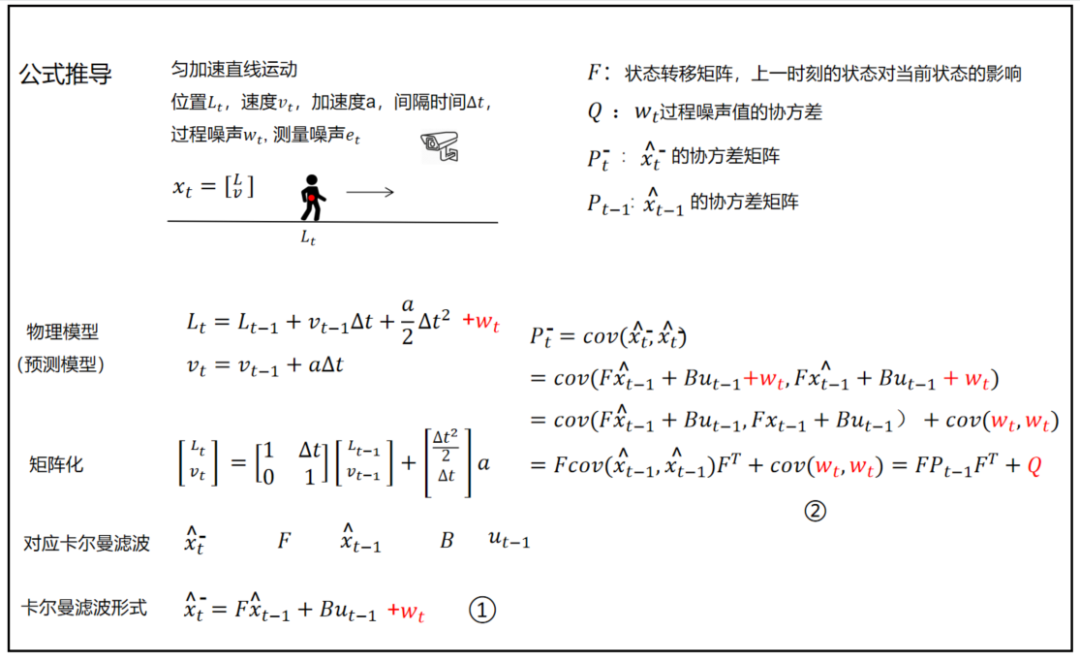
测量方程：

以上是预测的公式的推导，更新的公式推导稍微有点复杂，暂不推导，而是以理解为主。

6、卡尔曼滤波公式理解

修正估计也叫融合估计，也叫最优估计。

它是融合了预测值和测量值的结果。

而两个值如何融合就靠卡尔曼增益这个参数了，可以看成是这两个值的权重或者说信任度。

修正估计：

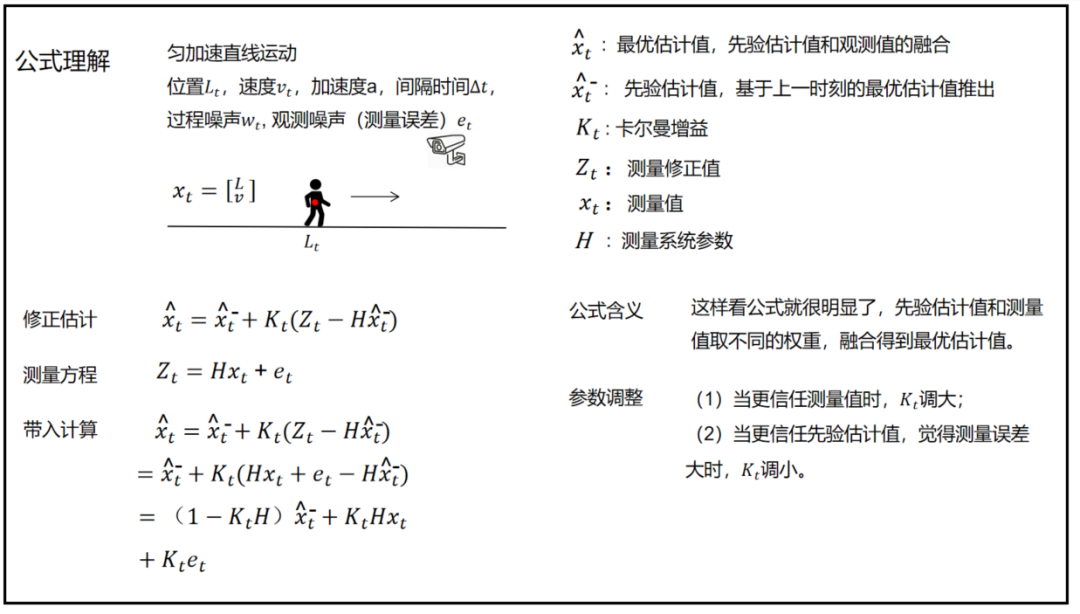
卡尔曼增益K实际上表征了状态最优估计过程中模型预测误差（Predicted error）与量测误差（Measurement error）的比重。

卡尔曼增益：

后验估计协方差：

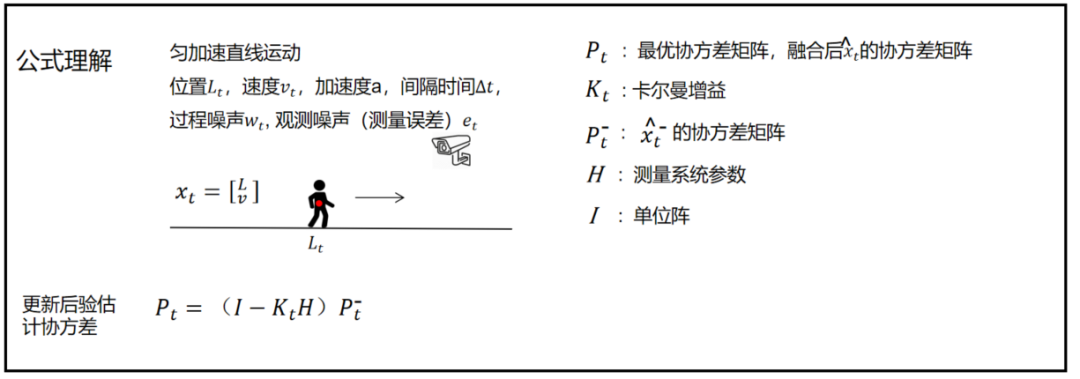
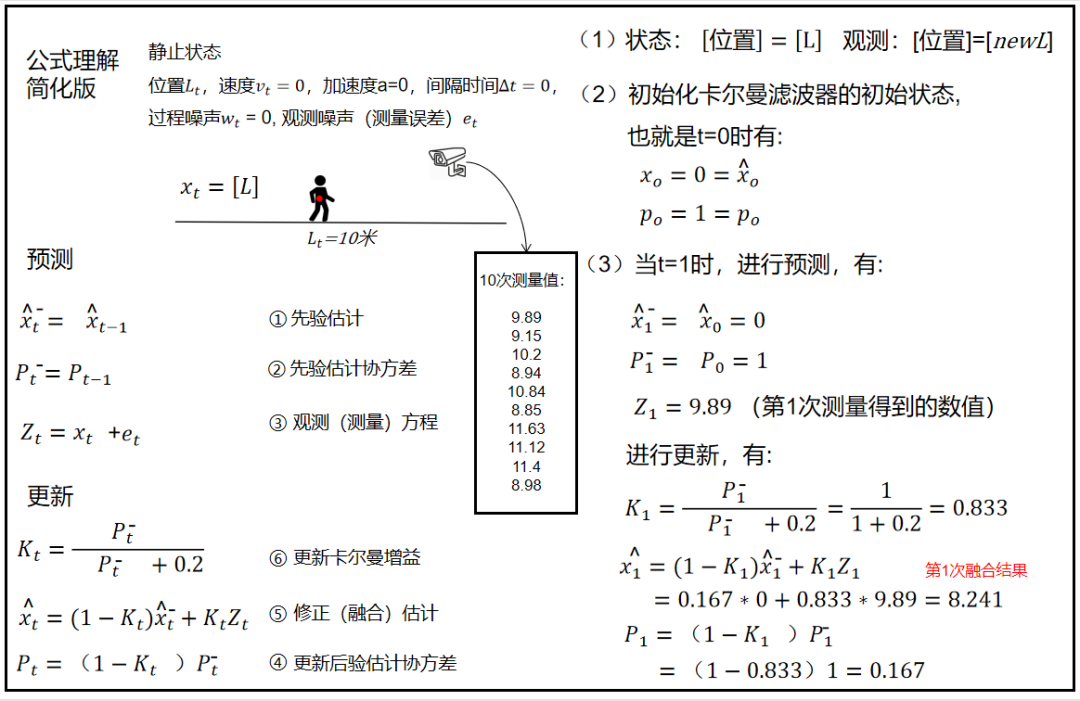
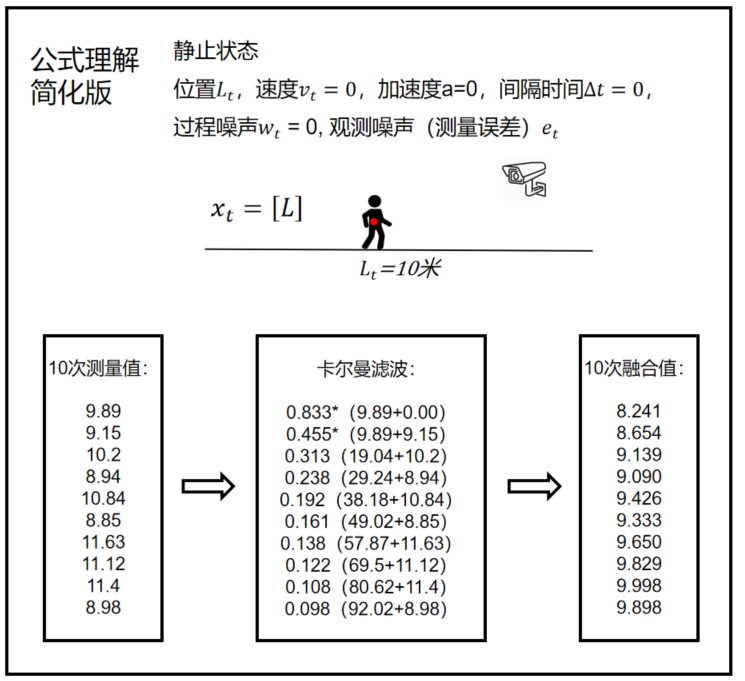
7、卡尔曼滤波简化版

卡尔曼滤波公式看起来很是复杂不好理解。

那么就进行化繁为简，看看它到底在干嘛。

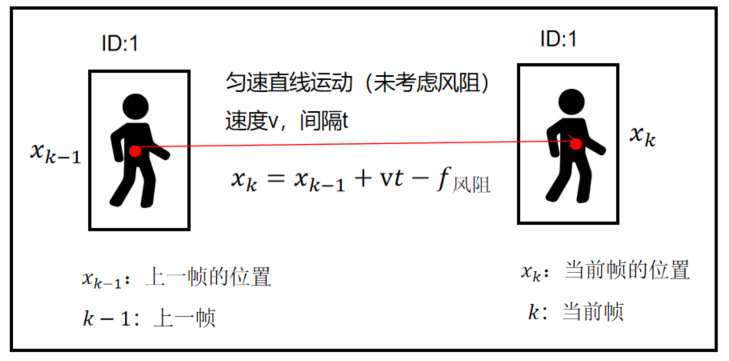
之前是匀加速直线运动，现在不加速了，不运动了，干脆静止吧。

这样就没有运动误差了，只有测量误差。

那就看你测的准不准了。

位置：由于静止，下一时刻的位置肯定等于上一时刻的位置等于初始位置。

且没有过程误差。

测量：依然存在测量误差，H等于1。

融合估计：H取1。

后验估计协方差：H取1。

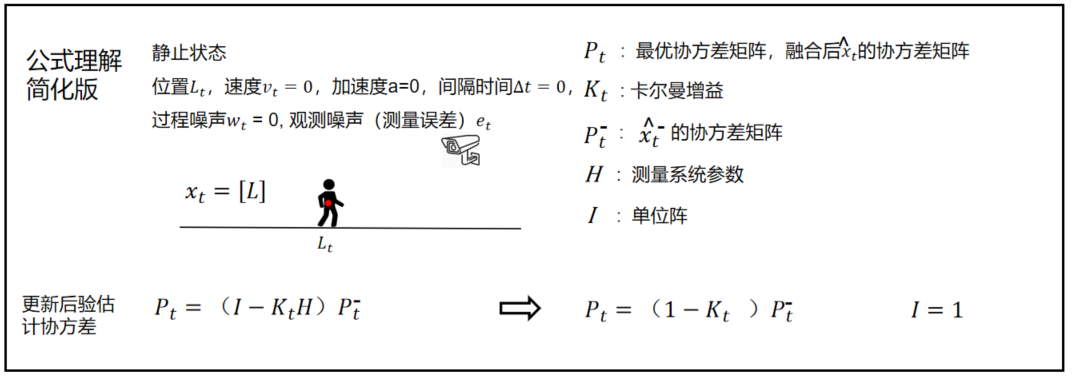
卡尔曼滤波匀加速直线运动和静止情况下公式对比：

简化版卡尔曼滤波过程：

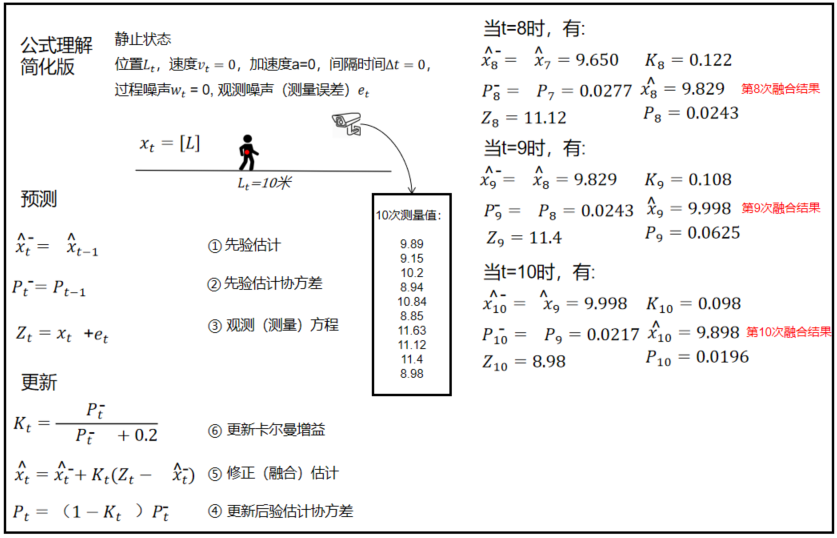
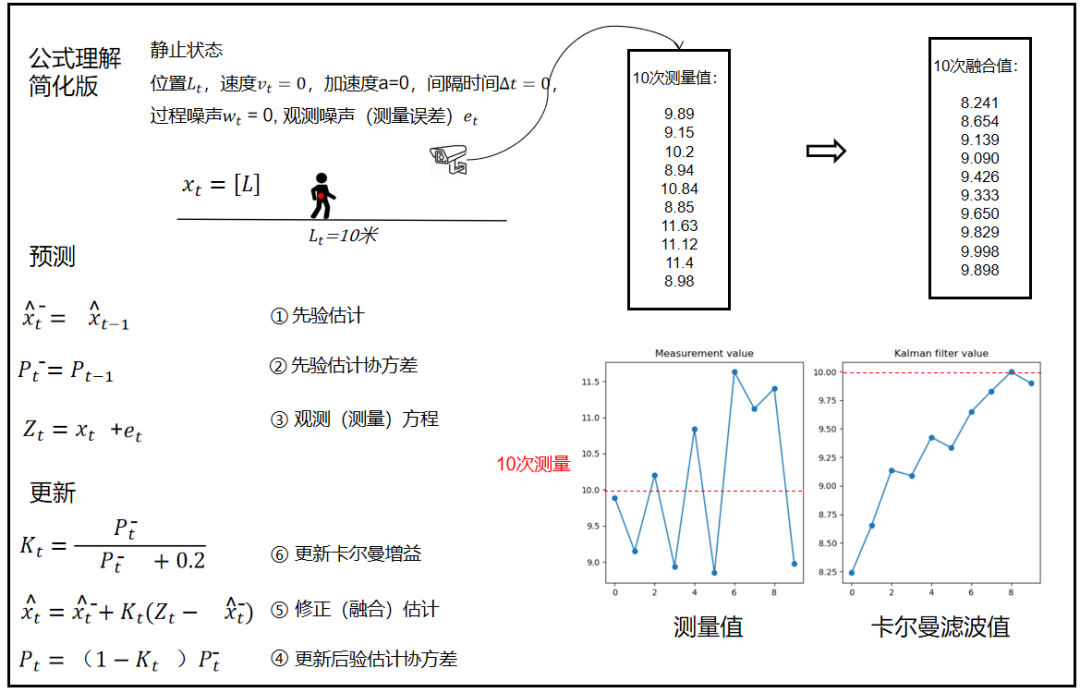
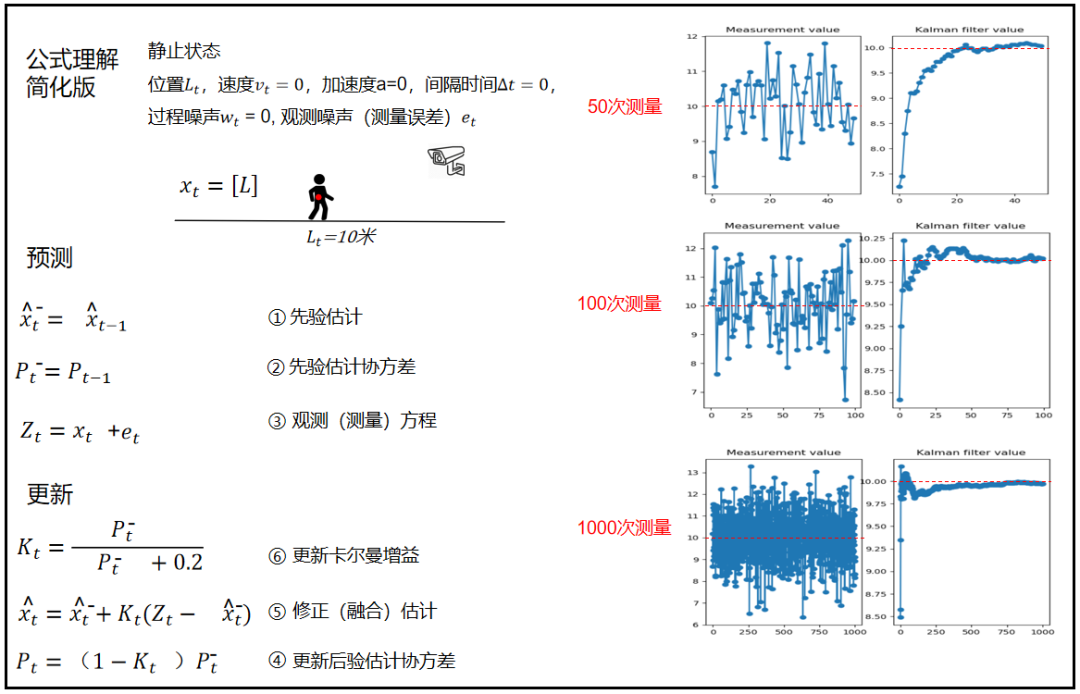
测量十次的时候卡尔曼滤波效果还不是很明显，当测量50次100次效果就出来了，在一定次数后的值明显不会偏离真实值很远。

这就是卡尔曼滤波达到的效果。

（50次，100次等每次的图不是一样的值，而是高斯分布随机生成的值，所以导致在数值上是不一样的。）

8、卡尔曼滤波简化版公式通式

进行融合估计值的计算：

最后发现相当于每个测量值权重一样了，只是权重相加不等于1，当然，当t很大的时候，就很接近1了。

卡尔曼滤波就是在求测量值的平均！

会不会是偶然所致？改变R=0.3试一下。

还是一样，权重一样，在求平均。

是什么导致了各个系数权重一样？

也就是说这个式子系数相等：

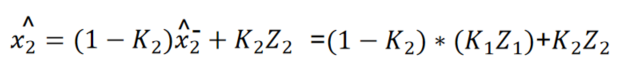
即（1-k2）k1=k2   ，即（1-kt）kt-1 =kt。

将K1的式子带入p1，最后得出一个通式：

证毕！

这就是为什么权重都一样的数学原因。

显然，当t趋于无穷大的时候，所有权重系数和就是1。

9、卡尔曼滤波类比

当我看到卡尔曼滤波的融合公式的时候，第一时间想到了Momentum的一阶动量公式，仿佛卡尔曼滤波的这个公式在哪里见过。

卡尔曼滤波能够利用前一时刻的状态和可能的测量值来得到当前时刻下的状态的最优估计。

卡尔曼滤波是一个根据未来输入不断变换并自我调整的过程。

动量梯度下降法是考虑了所有历史数据，只是分派了不同的权重，这个历史数据越近的数据权重越大。

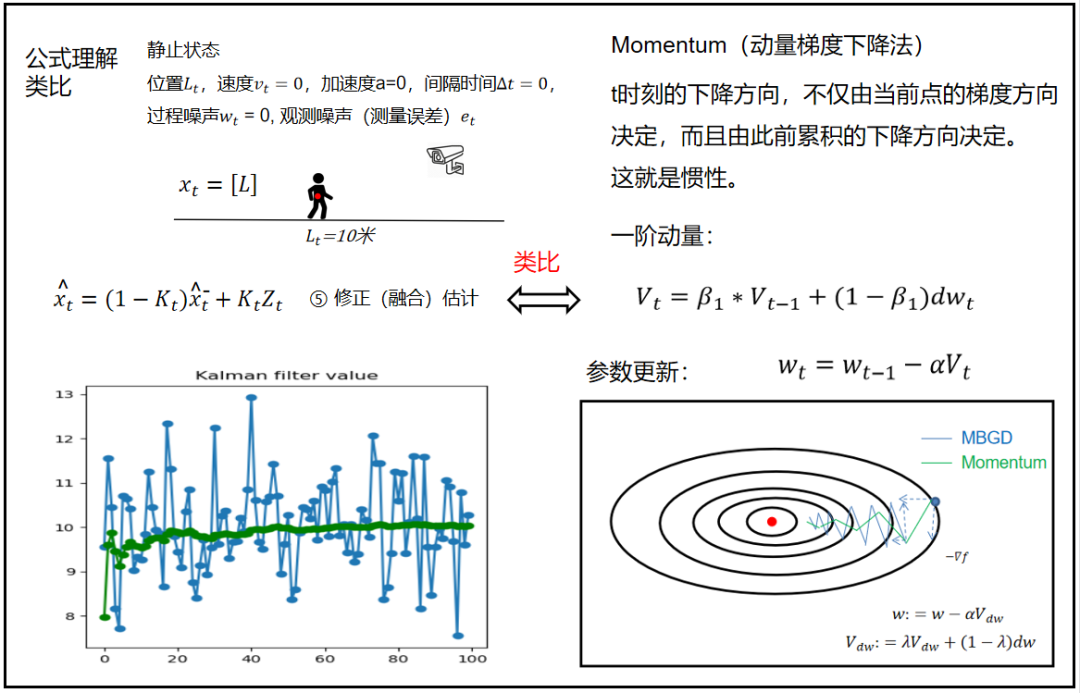
从图形上看：

Momentum，可以看成是MBGD的滤波，数值从两边压缩。

卡尔曼滤波，将测量值的上下波动，滤波成中间数值。

从公式上看：

Momentum，考虑了所有历史数据，这个历史数据越近的数据权重越大，太遥远的数据几乎可以忽略不计。

卡尔曼滤波，也考虑了所有历史数据，但这些历史数据权重一样，不可忽略。

10、卡尔曼滤波实例

上述忽略了过程噪声的影响，现在加上这个因素。

11、总结

目标跟踪中，在数据关联后往往要进行卡尔曼滤波。

数据关联算法得到了每个目标的观测数据。

卡尔曼滤波使用关联的观测数据来估计目标的状态，并预测目标的未来位置和速度等信息。

 ——————

浅谈则止，细致入微AI大道理

扫描下方“AI大道理”，选择“关注”公众号

—————————————————————

 

—————————————————————

投稿吧   | 留言吧