目录
一、理论基础
二、核心程序
三、测试结果
一、理论基础
1.1ESPRIT
ESPRIT算法全称为:Estimation of Signal Parameters using Rotational Invariance Techniques.与Root_MUSIC算法相同,也是一种参数估计技术。ESPRIT算法在旋转矢量中,一个元素上的信号来源于更早期元素信号的相移。ESPRIT推导如下:

 1.2 LS-ESPRIT
1.2 LS-ESPRIT
基于ESPRIT有两种经典的方法:最小二乘(LS)法和总体最小二乘(TLS)法。其推导过程如下所示:

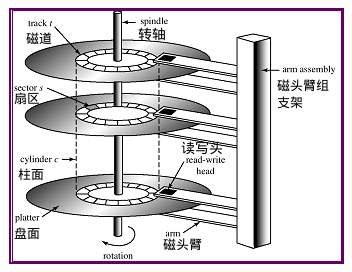
1.3 Music
MUSIC(Multiple Signal Classification),多重信号分类,是一类空间谱估计算法。其思想是利用接收数据的协方差矩阵(Rx)进行特征分解,分离出信号子空间和噪声子空间,利用信号方向向量与噪声子空间的正交性来构成空间扫描谱,进行全域搜索谱峰,从而实现信号的参数估计。
MUSIC算法是空间谱估计发展史上具有里程碑意义的算法,它实际上已经成为空间谱估计方法和理论的重要基石。其特点是测向分辨率高;对信号个数、DOA、极化、噪声干扰强度、来波的强度和相干关系可以进行渐近无偏估计;可以解决多径信号的DOA估计问题;可以用于高密度信号环境下的无线测向。如果噪声子空间大于信号子空间,MUSIC算法有更好的性能。
MUSIC算法是建立在以下假设基础上的:
(1)阵列形式为线性均匀阵,阵元间距不大于处理最高频率信号波长的二分之一;
(2)信号源数小于阵元的数目,以确保阵列流型矩阵的各个列线性独立;
(3)处理器的噪声为加性高斯分布,不同阵元间距噪声均为平稳随机过程,各阵元间噪声相互独立,空间平稳(各噪声方差相等);
(4)空间信号为零均值平稳随机过程,信号与阵源噪声与相互独立;
(5)信号源通常为窄带远场信号。正是由于MUSIC算法在特定的条件下具有很高的分辨力、估计精度及稳定性,从而吸引了大量的学者对其进行深入的研究和分析。
1.4 Root-Music
直接构造函数,并将噪声子空间的向量写成矩阵G,最终将信号频率估计问题转化成了一元高次方程的求根问题。在实际求解时,需要在2(M-1)个根中,找出其中位置最接近单位元的K个根,其相位就是信号频率的估计值。

二、核心程序
......................................................
st=randn(Q,K)+j*randn(Q,K);% 任意产生一个2行100列的复矩阵
SNR=10;
Pn=1;% 噪声能量为1
Ps=10^(SNR/10);% 信噪比公式 SNR=10log(Ps/Pn)
stt=sqrt(Ps/2)*st;
nt=sqrt(Pn/2)*(randn(N,K)+j*randn(N,K));
xt=A*stt+nt
RX=(xt*xt')/K;
RN=(nt*nt')/K;
[a1 d1]=eig(RX,RN)
Us=a1(:,N-1:N);
Us1=Us(1:N-1,:);
Us2=Us(2:N,:);
F=pinv(Us1);
FI=F*Us2;
[a d]=eig(FI)
x=-angle(d);
y=asin(x./pi);
ans=(y.*180)./pi
temp4=-90:0.1:90;
......................................................三、测试结果
使用matlab2021a仿真测试结果如下所示:
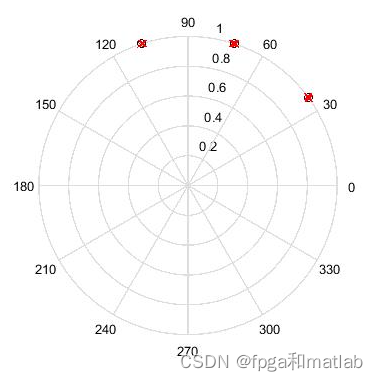
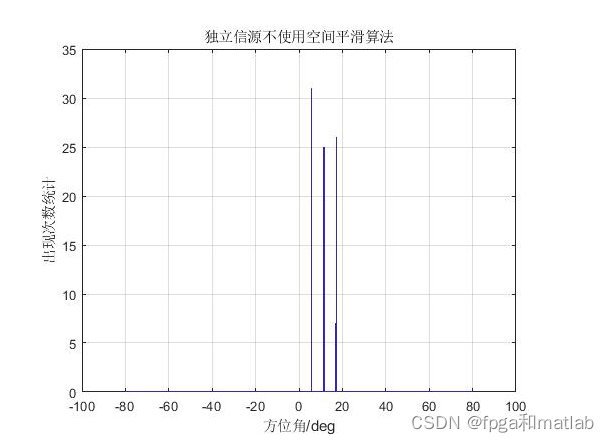



up00011



![[oeasy]python0027_整合程序_延迟输出时间_整合两个py程序](https://img-blog.csdnimg.cn/img_convert/18454516a5d87a12b4e7156b7207a07c.png)