2.4 线性表的插入删除

news2024/10/6 0:31:11

1. 链表的插入删除

1. 单链表插入删除

图1. 单链表插入结点

 图2. 单链表删除结点

#include <iostream>

typedef struct LNode {
    int data;
    struct LNode* next;
}LNode;


/// <summary>
/// 判断链表是否非空
/// </summary>
/// <param name="p"></param>
bool linkedListIsNotNull(LNode* p) {
    if (p == NULL) {
        return false;
    }
    return true;
}

/// <summary>
/// 遍历输出链表各个结点的值
/// </summary>
/// <param name="firstNode"></param>
void traverseLinkedList(LNode* p) {
    while (p != NULL) {
        // 对当前节点进行操作，打印节点的数据
        printf("%d\n", p->data);

        // 移动到下一个节点
        p = p->next;
    }
}

/// <summary>
/// 插入元素
/// </summary>
/// <param name="p">插入位置前面的元素</param>
/// <param name="q">要插入的元素</param>
void insertElement(LNode* p, LNode* q) {
    q->next = p->next;
    p->next = q;
}

/// <summary>
/// 删除元素
/// </summary>
/// <param name="p">要删除的元素的前一个元素</param>
/// <returns></returns>
LNode* deleteElement(LNode* p) {
    LNode* q = p->next;
    p->next = q->next;
    q->next = NULL;
    return q;
}

int main()
{
    LNode* A;
    A = new LNode;
    LNode* B;
    B = new LNode;
    LNode* C;
    C = new LNode;

    A->data = 10;
    B->data = 20;
    C->data = 30;

    A->next = B;
    B->next = NULL;
    C->next = NULL;

    LNode* p = A;
    LNode* q = C;
    bool isNotNull = linkedListIsNotNull(p);
    if (isNotNull) {
        insertElement(p, q);
        traverseLinkedList(p);
        printf("---------------------------\n");
        LNode* q = deleteElement(p);
        free(q);
        traverseLinkedList(p);
    }
    else {
        printf("链表为空!");
    }
}

代码1: 单链表的插入删除(没有考虑特殊情况)

        特殊情况: 在链表的第一个结点之前插入结点或者删除第一个结点. 

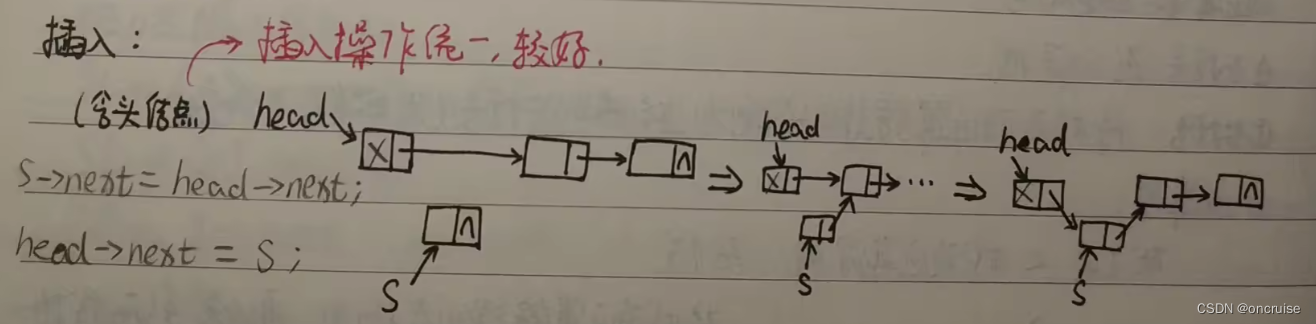
图3. 在含头结点的单链表的第一个结点之前插入结点

 图4. 在不含头结点的单链表的第一个结点之前插入结点

图5. 含头结点的单链表删除第一个结点

 图6. 不含头结点的单链表删除第一个结点

#include <iostream>

typedef struct LNode {
    int data;
    struct LNode* next;
}LNode;


/// <summary>
/// 判断链表是否非空
/// </summary>
/// <param name="p"></param>
bool linkedListIsNotNull(LNode* p) {
    if (p == NULL) {
        return false;
    }
    return true;
}

/// <summary>
/// 遍历输出链表各个结点的值
/// </summary>
/// <param name="firstNode"></param>
void traverseLinkedList(LNode* p) {
    while (p != NULL) {
        // 对当前节点进行操作，打印节点的数据
        printf("%d\n", p->data);

        // 移动到下一个节点
        p = p->next;
    }
}

/// <summary>
/// 插入元素
/// </summary>
/// <param name="p">插入位置前面的元素</param>
/// <param name="q">要插入的元素</param>
void insertElement(LNode* p, LNode* q) {
    q->next = p->next;
    p->next = q;
}

/// <summary>
/// 第一个结点之前插入元素
/// </summary>
/// <param name="p">第一个结点</param>
/// <param name="q">要插入的元素</param>
void insertFirstElement(LNode*& p, LNode* q) {   //在C++中，指针类型属于值类型。这里需要改变p的值, 因此传递p的引用
    q->next = p;
    p = q;
    printf("第一个数据: %d\n", p->data);
}

/// <summary>
/// 删除元素
/// </summary>
/// <param name="p">要删除的元素的前一个元素</param>
/// <returns></returns>
LNode* deleteElement(LNode* p) {
    LNode* q = p->next;
    p->next = q->next;
    q->next = NULL;
    return q;
}

/// <summary>
/// 删除第一个结点
/// </summary>
/// <param name="p">第一个结点</param>
/// <returns></returns>
LNode* deleteFirstElement(LNode*& p) {  //在C++中，指针类型属于值类型。这里需要改变p的值, 因此传递p的引用
    LNode* q = p;
    p = p->next;
    printf("删除的第一个数据: %d\n", q->data);
    return q;
}

int main()
{
    LNode* A;
    A = new LNode;
    LNode* B;
    B = new LNode;
    LNode* C;
    C = new LNode;

    A->data = 10;
    B->data = 20;
    C->data = 30;

    A->next = B;
    B->next = NULL;
    C->next = NULL;

    LNode* p = A;
    LNode* q = C;
    bool isNotNull = linkedListIsNotNull(p);
    if (isNotNull) {
        insertFirstElement(p, q);
        traverseLinkedList(p);
        printf("---------------------------\n");
        LNode* q = deleteFirstElement(p);
        free(q);
        traverseLinkedList(p);
    }
    else {
        printf("链表为空!");
    }
}

代码2: 在不含头结点的单链表的第一个结点之前插入结点或者删除第一个结点. 

        需要注意的是, 在C++中，指针类型属于值类型。在第一个结点之前插入结点或者删除第一个结点的函数中需要改变p的值, 因此传递p的引用. 

#include <iostream>

typedef struct LNode {
    int data;
    struct LNode* next;
}LNode;


/// <summary>
/// 判断链表是否非空
/// </summary>
/// <param name="p"></param>
bool linkedListIsNotNull(LNode* p) {
    if (p == NULL) {
        return false;
    }
    return true;
}

/// <summary>
/// 遍历输出链表各个结点的值
/// </summary>
/// <param name="firstNode"></param>
void traverseLinkedList(LNode* p) {
    while (p != NULL) {
        // 对当前节点进行操作，打印节点的数据
        if (p->data != 0) {
            printf("%d\n", p->data);
        }

        // 移动到下一个节点
        p = p->next;
    }
}

/// <summary>
/// 插入元素
/// </summary>
/// <param name="p">插入位置前面的元素</param>
/// <param name="q">要插入的元素</param>
void insertElement(LNode* p, LNode* q) {
    q->next = p->next;
    p->next = q;
}

/// <summary>
/// 删除元素
/// </summary>
/// <param name="p">要删除的元素的前一个元素</param>
/// <returns></returns>
LNode* deleteElement(LNode* p) {
    LNode* q = p->next;
    p->next = q->next;
    q->next = NULL;
    return q;
}

int main()
{
    LNode* H;
    H = new LNode;
    LNode* A;
    A = new LNode;
    LNode* B;
    B = new LNode;
    LNode* C;
    C = new LNode;

    H->data = NULL;
    A->data = 10;
    B->data = 20;
    C->data = 30;

    H->next = A;
    A->next = B;
    B->next = NULL;
    C->next = NULL;

    LNode* p = H;   //p指向头结点
    LNode* q = C;
    bool isNotNull = linkedListIsNotNull(p);
    if (isNotNull) {
        //第一个结点之前即头结点之后插入元素
        insertElement(p, q);
        traverseLinkedList(p);
        printf("---------------------------\n");
        //删除第一个结点, 即删除头结点之后的元素
        LNode* q = deleteElement(p);
        free(q);
        traverseLinkedList(p);
    }
    else {
        printf("链表为空!");
    }
}

代码3: 在含头结点的单链表的第一个结点之前插入结点或者删除第一个结点. 

        可以看出: 给链表设置头结点, 可以使得在第一个数据结点之前插入一个新结点和删除第一个数据结点的操作同表中部结点的这些操作统一起来, 方便写代码; 带头结点的链表, 其头指针值不随操作而改变, 可以减少错误. 

2. 双链表插入删除

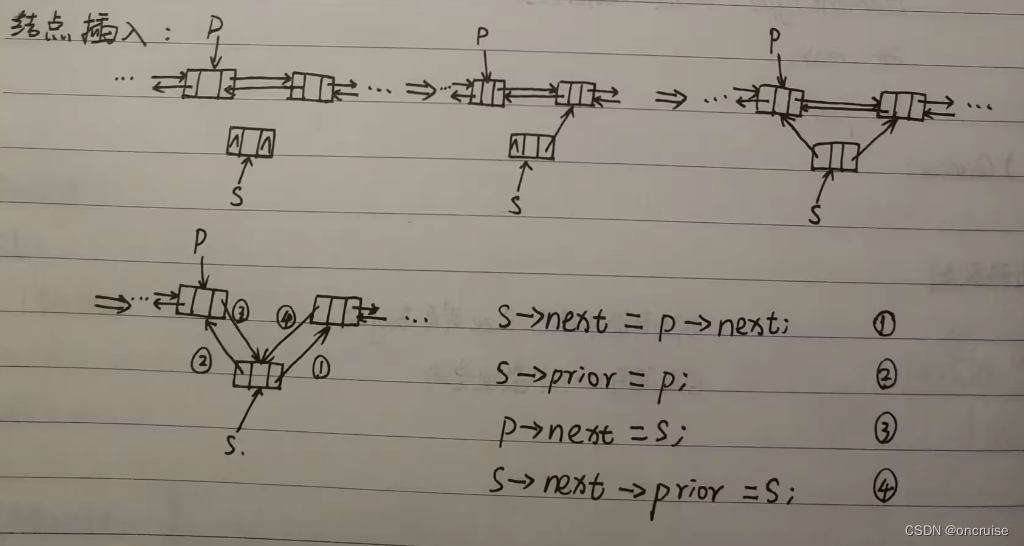
 图7. 双链表结点插入

图8. 双链表结点删除

#include <iostream>

typedef struct LNode {
    int data;
    struct LNode* next;
    struct LNode* prior;
}LNode;

/// <summary>
/// 遍历输出链表各个结点的值
/// </summary>
/// <param name="firstNode"></param>
void traverseLinkedList(LNode* p) {
    p = p->next;
    while (p != NULL) {
        // 对当前节点进行操作，打印节点的数据
        printf("%d\n", p->data);

        // 移动到下一个节点
        p = p->next;
    }
}

/// <summary>
/// 判断链表是否非空
/// </summary>
/// <param name="p"></param>
bool linkedListIsNotNull(LNode* p) {
    if (p->next == NULL) {
        return false;
    }
    return true;
}

/// <summary>
/// 插入元素
/// </summary>
/// <param name="p">插入位置前面的元素</param>
/// <param name="s">要插入的元素</param>
void insertElement(LNode* p, LNode* s) {
    s->next = p->next;
    s->prior = p;
    p->next = s;
    s->next->prior = s;
}

/// <summary>
/// 删除元素
/// </summary>
/// <param name="s">要删除的元素</param>
/// <returns></returns>
LNode* deleteElement(LNode* s) {
    s->prior->next = s->next;
    s->next->prior = s->prior;

    s->next = NULL;
    s->prior = NULL;
    return s;
}


int main()
{
    LNode* H;
    H = new LNode;
    LNode* A;
    A = new LNode;
    LNode* B;
    B = new LNode;
    LNode* C;
    C = new LNode;

    H->data = NULL;
    A->data = 10;
    B->data = 20;
    C->data = 30;

    H->next = A;
    A->next = B;
    B->next = NULL;
    C->next = NULL;

    H->prior = NULL;
    A->prior = H;
    B->prior = A;
    C->prior = NULL;

    LNode* p = H;        
    LNode* s = C;
    bool isNotNull = linkedListIsNotNull(p);
    if (isNotNull) {
        insertElement(p, s);
        traverseLinkedList(p);
        printf("---------------------------\n");
        LNode* q = deleteElement(s);
        free(q);
        traverseLinkedList(p);
    }
    else {
        printf("链表为空!");
    }
}

代码4: 在含头结点的双链表的第一个结点之前插入结点或者删除第一个结点. 

        可以看出, 在双链表里要删除一个结点, 我们只需要知道这个结点的地址信息即可, 因为其相邻的结点的地址信息已在该结点的内部储存. 

2. 顺序表的插入删除

1. 顺序表的插入操作

 图9. 顺序表插入元素

        可插入下标位置p的取值范围是: 0到length; 

        当表长length等于数组长度maxSize的时候, 不可以再插入元素; 

        移动元素从后往前后移; 

        接下来写一个可以在顺序表中任一位置合法地插入一个新元素的函数. 所谓合法, ①插入元素的位置必须合法, 即0 <= p <= length; ②插入元素的时机必须合法, 即length < maxSize. 

#include <iostream>

/// <summary>
/// 数组最大长度
/// </summary>
const int MAX_SIZE = 10;

/// <summary>
/// 顺序表插入元素
/// </summary>
/// <param name="arr">要操作的数组</param>
/// <param name="length">插入元素前的数组长度</param>
/// <param name="p">插入位置</param>
/// <param name="e">插入元素</param>
/// <returns></returns>
int insertElement(int* arr, int& length, int p, int e) {
    if (p < 0 || p > length || length > MAX_SIZE) {
        return 0;       //不合法
    }
    for (int i = length - 1; i >= p; i--)       //注意这里是i--
    {
        arr[i + 1] = arr[i];
    }
    arr[p] = e;
    length++;
    return 1;
}

int main()
{
    int arr[MAX_SIZE] = { 1,2,3,4,5,6 };
    int length = 6;

    int result = insertElement(arr, length, 0, 9999);

    if (result == 1) {
        for (int i = 0; i < length; i++)
        {
            printf("%d\n", arr[i]);
        }
    }
}

代码5: 顺序表插入元素

2. 顺序表的删除操作

图10. 顺序表删除元素

        注意, 若强行修改length的值, 如将length修改为3, 其它的不变, 则此时顺序表所存的线性表中的元素只有0, 1, 2中的元素, 其它的元素虽然也在数组中, 但是它们已经不属于该顺序表中的元素了. 0 ~ length - 1才是顺序表中的元素所在范围. 除此之外的都不算顺序表中的元素. 

        所以如果想将顺序表清零, 只需length = 0即可. 其它的不用管, 虽然那些元素还留在数组中, 但对于该顺序表来说, 它是不可见的. 

        可删除元素下标p的取值范围: 0 ~ length - 1; 

        当表长length等于0时, 不可以再删除元素; 

        移动元素从前往后前移; 

#include <iostream>

/// <summary>
/// 数组最大长度
/// </summary>
const int MAX_SIZE = 10;

/// <summary>
/// 顺序表插入元素
/// </summary>
/// <param name="arr">要操作的数组</param>
/// <param name="length">插入元素前的数组长度</param>
/// <param name="p">插入位置</param>
/// <param name="e">插入元素</param>
/// <returns></returns>
int insertElement(int* arr, int& length, int p, int e) {
    if (p < 0 || p > length || length > MAX_SIZE) {
        return 0;       //不合法
    }
    for (int i = length - 1; i >= p; i--)       //注意这里是i--
    {
        arr[i + 1] = arr[i];
    }
    arr[p] = e;
    length++;
    return 1;
}

/// <summary>
/// 顺序表删除元素
/// </summary>
/// <param name="arr">要操作的数组</param>
/// <param name="length">数组删除元素前的长度</param>
/// <param name="p">要删除的位置</param>
/// <param name="e">要删除的元素</param>
/// <returns></returns>
int deleteElement(int* arr, int& length, int p, int& e) {
    if (p < 0 || p > length - 1 || length <= 0) {
        return 0;
    }
    e = arr[p];
    for (int i = p; i < length - 1; i++)
    {
        arr[i] = arr[i + 1];
    }
    length--;
    return 1;
}

int main()
{
    int arr[MAX_SIZE] = { 1,2,3,4,5,6 };
    int length = 6;
    int e;
    int result = deleteElement(arr, length, 0, e);

    if (result == 1) {
        printf("删除的元素: %d\n", e);
        for (int i = 0; i < length; i++)
        {
            printf("%d\n", arr[i]);
        }
    }
}

代码6: 顺序表删除元素

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/757534.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

常见关于数组的函数的介绍

常见关于数组的函数的介绍

关于字符串函数的介绍 求字符串长度 strlen函数 用于计算字符串的长度的函数&#xff0c;需要使用的库函数是string.h 函数声明 size_t strlen(const char *str)函数模拟实现 #include<stdio.h> #include<assert.h> size_t my_strlen(const char* arr) {asse…
阅读更多...
review回文子串

review回文子串

给你一个字符串 s&#xff0c;请你将 s 分割成一些子串&#xff0c;使每个子串都是 回文串 。返回 s 所有可能的分割方案。 回文串 是正着读和反着读都一样的字符串。 class Solution {List<List<String>> lists new ArrayList<>(); // 用于存储所有可能…
阅读更多...
阿里瓴羊One推出背后，零售企业迎数字化新解

阿里瓴羊One推出背后，零售企业迎数字化新解

配图来自Canva可画 近年来随着数字经济的高速发展&#xff0c;各式各样的SaaS应用服务更是层出不穷&#xff0c;但本质上SaaS大多局限于单一业务流层面&#xff0c;对用户核心关切的增长问题等则没有提供更好的解法。在SaaS赛道日渐拥挤、企业增长焦虑愈演愈烈之下&#xff0c…
阅读更多...
Midjourney助力交互设计师设计网站主页

Midjourney助力交互设计师设计网站主页

Midjourney的一大核心优势是提供创意设计&#xff0c;这个功能也可以用在网站主页设计上&#xff0c;使用Midjourney prompt 应尽量简单&#xff0c;只需要以"web design for..." or "modern web design for..."开头即可 比如设计一个通用SAAS服务的初创企…
阅读更多...
单片机第一季：零基础5——LED点阵

单片机第一季：零基础5——LED点阵

1&#xff0c;第八章-LED点阵 如何驱动LED点阵&#xff1a; (1)单片机端口直接驱动。要驱动8*8的点阵需要2个IO端口&#xff08;16个IO口&#xff09;、要驱动16*16的点阵需要4个IO端口&#xff08;32个IO口&#xff09;。 (2)使用串转并移位锁存器驱动。要驱动16*16点阵只需要…
阅读更多...
Linux 系统编程-开发环境(二）

Linux 系统编程-开发环境(二）

目录 7 压缩包管理 7.1 tar 7.2 rar 7.3 zip 8 进程管理 8.1 who 8.2 ps 8.3 jobs 8.4 fg 8.5 bg 8.6 kill 8.7 env 8.8 top 9 用户管理 9.1 创建用户 9.2 设置用户组 9.3 设置密码 9.4 切换用户 9.5 root用户 9.6 删除用户 10 网络管理 10.1 i…
阅读更多...
MySQL-分库分表详解（七）

MySQL-分库分表详解（七）

♥️作者&#xff1a;小刘在C站 ♥️个人主页&#xff1a; 小刘主页 ♥️努力不一定有回报&#xff0c;但一定会有收获加油&#xff01;一起努力&#xff0c;共赴美好人生&#xff01; ♥️学习两年总结出的运维经验&#xff0c;以及思科模拟器全套网络实验教程。专栏&#xf…
阅读更多...
【熬夜送书 | 第二期】清华社赞助 | 《前端系列丛书》

【熬夜送书 | 第二期】清华社赞助 | 《前端系列丛书》

前端是什么? 前端&#xff08;Front-End&#xff09;&#xff0c;又称浏览器端、客户端等&#xff0c;是指 Web 应用程序中负责用户交互、界面展示和数据展示的部分。前端技术体系主要包括 HTML、CSS 和 JavaScript 等内容。 其中&#xff0c;HTML&#xff08;Hypertext Mar…
阅读更多...
❀如何获得铁粉❀

❀如何获得铁粉❀

文章目录 引言一、提供独特的价值1.1 分享专业知识和经验1.2 提供独特的产品或服务1.3 展示个人风格和个性 二、构建真实的关系2.1 回应评论和互动2.2 分享个人故事和经历2.3 建立信任和互信关系 三、提供独家福利3.1 提供折扣和促销3.2 推出限量版产品或服务3.3 独家活动和会员…
阅读更多...
位运算常见算法题

位运算常见算法题

文章目录 前言191. 位1的个数338. 比特位计数461. 汉明距离136. 只出现一次的数字260. 只出现一次的数字 III面试题 01.01. 判定字符是否唯一268. 丢失的数字371. 两整数之和137. 只出现一次的数字 II面试题 17.19. 消失的两个数字 前言 本篇文章会涉及多道位运算题目&#xf…
阅读更多...
图像处理学习笔记（一）

图像处理学习笔记（一）

目录 图像处理学习笔记&#xff08;一&#xff09;一、基础知识1、彩色图像&#xff08;1&#xff09;RGB&#xff08;2&#xff09;HSV&#xff08;3&#xff09;HSI&#xff08;4&#xff09;CMYK&#xff08;5&#xff09;YUV&#xff08;6&#xff09;YCbCr 2、灰度图像3、…
阅读更多...
谋合作、创新境 | 百度参观图为科技生产全链路

谋合作、创新境 | 百度参观图为科技生产全链路

当代科技的发展不断催生出新的变革和机遇&#xff0c;百度作为全球顶尖的高科技公司&#xff0c;凭借其强大的创新基因&#xff0c;一直处于人工智能领域的最前沿。 　　近日&#xff0c;百度公司派出了一支专业团队来到了图为科技&#xff0c;对图为的研发技术及生产线进行了全…
阅读更多...
python 把txt文本的log日志倒序处理

python 把txt文本的log日志倒序处理

在上述代码中&#xff0c;我们尝试了一系列常见的编码&#xff08;utf-8、gbk、latin-1&#xff09;来打开文件&#xff0c;直到找到一个能够成功解码文件内容的编码。 如果找到了匹配的编码&#xff0c;就使用该编码读取文件内容。如果仍然出现解码错误&#xff0c;你可能需要…
阅读更多...
虚幻Voxel插件

虚幻Voxel插件

虚幻Voxel插件 Voxel Plugin Voxel Plugin brings smoothed voxel terrain to Unreal Engine 4. Generate, destroy and terraform the world! 体素插件可以在虚幻引擎中生成平滑的体素地形。创造、破环和改造世界。 Terrain generation and terraforming both in game and i…
阅读更多...
CANOE 操作详情

CANOE 操作详情

canoe 手把手教你如何操作canoe工具&#xff1a; 1&#xff1a;创建test文件夹&#xff0c; 并在文件夹下创建3 文件夹 2&#xff1a;创建canoe工程&#xff0c;选择500波特率 3: 双击后进入 4&#xff1a;创建DBC文件 5 创建网络节点&#xff1a; 两个节点创建好之后&#x…
阅读更多...
mpVue 微信小程序基于vant-weapp 组件的二次封装TForm 表单组件（适配移动端）——新增仓库地址

mpVue 微信小程序基于vant-weapp 组件的二次封装TForm 表单组件（适配移动端）——新增仓库地址

一、前言 1、mpVue微信小程序不支持动态组件&#xff08;<component> &#xff09; 2、mpVue微信小程序不支持动态属性及事件穿透&#xff08;$attrs和$listeners&#xff09; 3、mpVue微信小程序不支持render函数 二、最终效果 三、配置参数&#xff08;Attributes&…
阅读更多...
OpenCV for Python 入坑第一天：图像的基础操作

OpenCV for Python 入坑第一天：图像的基础操作

我们都知道&#xff0c;OpenCV能够帮助我们处理视频和图像&#xff0c;咱们在图像处理中&#xff0c;除了Pillow库之外&#xff0c;最经常用到的也是它了。那么现在咱们就正式入坑OpenCV for Python&#xff0c;一起来感受一下OpenCV的魅力吧&#xff01; 文章目录 读取图像 im…
阅读更多...
深入了解Redis-基础篇

深入了解Redis-基础篇

文章目录 一、故事背景二、知识点主要构成2.1、redis简介2.2、基于CentOS Linux docker容器化安装redis2.3、redis的数据类型2.3.1、String类型2.3.2、Hash类型2.3.3、List类型2.3.4、Set类型2.3.5、SortedSet类型 2.4、Redis的Java客户端2.4.1、Jedis2.4.1.1、Jedis的使用步骤…
阅读更多...
leetcode 572. 另一棵树的子树(java)

leetcode 572. 另一棵树的子树(java)

另一棵树的子树 另一棵树的子树题目描述解法一 DFS解法二 KMP 算法 KMP 算法 另一棵树的子树 来源&#xff1a;力扣&#xff08;LeetCode&#xff09; 链接&#xff1a;https://leetcode.cn/problems/subtree-of-another-tree 题目描述 给你两棵二叉树 root 和 subRoot 。检验 …
阅读更多...
脑电微状态方法可靠吗？

脑电微状态方法可靠吗？

摘要 EEG微状态是在静息态EEG记录中观察到的代表功能性脑网络的状态&#xff0c;在快速切换到另一个网络之前保持稳定40-120ms。人们认为微状态特征(如持续时间、发生率、覆盖率和转换概率)可以作为精神和神经系统疾病以及心理社会特征的神经标志物。然而&#xff0c;需要可靠…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023