0. 前言

按照国际惯例，首先声明：本文只是我自己学习的理解，虽然参考了他人的宝贵见解，但是内容可能存在不准确的地方。如果发现文中错误，希望批评指正，共同进步。

本文旨在通过实例验证权重衰减法（L2范数正则化方法）对深度学习神经元网络模型训练过程中出现的过拟合现象的抑制作用，加深对这个方法的理解。

1. 权重衰减方法作用

在训练神经元网络模型时，如果训练样本不足或者网络模型过于复杂，往往会导致训练误差可以快速收敛，但是在测试数据集上的泛化误差很大，即出现过拟合现象。

出现这种情况当然可以通过增多训练样本数来解决，但是如果增加额外的训练数据很困难，对应这类过拟合问题常用方法就是权重衰减法。

2. 权重衰减方法原理介绍

权重衰减等价于L2范数正则化，其方法是在损失函数中增加权重的L2范数作为惩罚项。以MSE均方误差为例，原本损失函数应该是：

$$loss=\frac{1}{n}\Sigma (y-\hat{y}{)}^2$$

增加L2范数后变成：

$$loss=\frac{1}{n}\Sigma (y-\hat{y}{)}^2+\frac{\lambda }{2n}||w|{|}^2$$
其中$||w|{|}^2$代表权重的二范数，$\lambda$为权重二范数的系数，$\lambda$≥0。

可以见得，如果$\lambda$越大，权重的“惩罚力度”就越大，权重$w$的绝对值就越接近0，如果$\lambda$=0，相当于没有“惩罚力度”。

3. 验证权重衰减法实例说明

3.1 训练数据样本

本次演示实例使用的输入训练数据为x_train = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]，输出训练数据为y_train = [0.52, 8.54, 6.94, 20.76, 32.17, 30.65, 40.46, 80.12, 75.12, 98.83]。

这个数据集是由$y=x^2$函数增加一个噪声数据生成得出，可以理解为$y=x^2$为该实例的真实解析解（真实规律）。

3.2 网络模型

使用torch.nn.Sequential()构建6层全连接层网络，每层神经元个数为：
InputLayer = 1，HiddenLayer1 = 3，HiddenLayer2 = 5，HiddenLayer3 = 10，HiddenLayer4 = 5，OutputLayer = 1

3.3 损失函数

选择MSE均方差损失函数，使用 torch.norm()计算权重的L2范数。

3.4 训练参数

无论是否增加L2范数惩罚项，训练参数都是一样的（控制变量）：优化函数选用torch.optim.Adam()，学习速率lr=0.005，训练次数epoch=3000。

4. 结果对比

增加L2范数学习结果为：

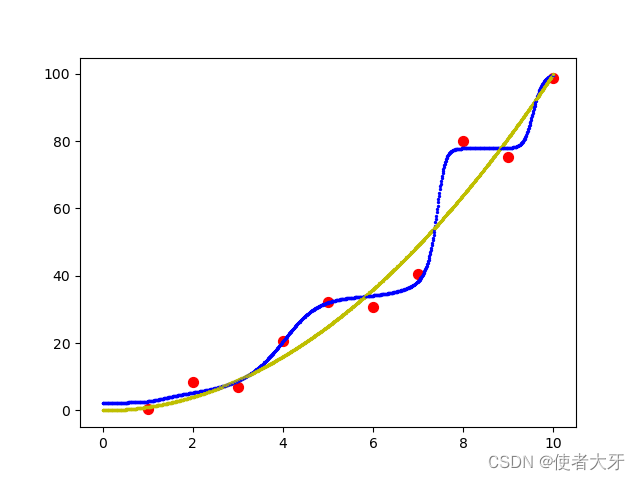
其中红点为训练数据；黄色线为解析解，即$y=x^2$；蓝色线为训练后的模型在$x=[0,10]$上的预测结果。

不加L2惩罚项的学习结果为：

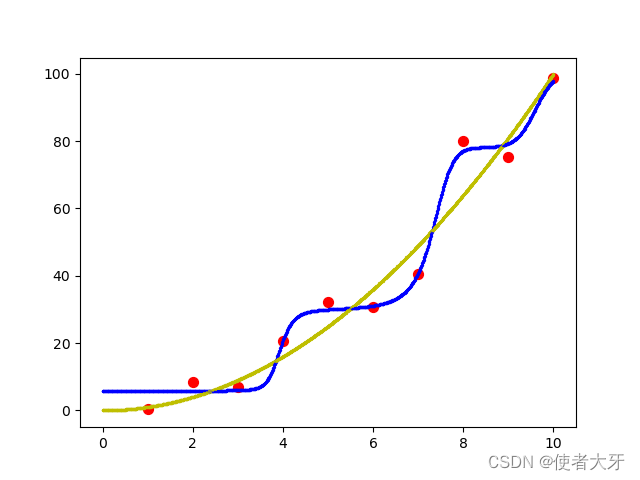
可以见得增加L2范数惩罚项后，测试的输出数据可以明显更贴合$y=x^2$理论曲线，尤其是在0~4范围上。

这里也可以增加一个类似损失函数的方式通过数据说明增加L2范数后学习结果更好，定义为：

$$loss=\Sigma \frac{(y-\hat{y}{)}^2}{{\hat{y}}^2}$$
其中$\hat{y}$为网络模型的输出结果，$y=x^2$

不加L2范数惩罚项$los{s}_{withoutL2}=183.65$
增加L2范数惩罚项后$los{s}_{withL2}=115.70$

5. 源码

import torch
import matplotlib.pyplot as plt

torch.manual_seed(25)

x_train = torch.tensor([1,2,3,4,5,6,7,8,9,10],dtype=torch.float32).unsqueeze(-1)
y_train = torch.tensor([0.52,8.54,6.94,20.76,32.17,30.65,40.46,80.12,75.12,98.83],dtype=torch.float32).unsqueeze(-1)
plt.scatter(x_train.detach().numpy(),y_train.detach().numpy(),marker='o',s=50,c='r')

class Linear(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.layers = torch.nn.Sequential(
            torch.nn.Linear(in_features=1, out_features=3),
            torch.nn.Sigmoid(),
            torch.nn.Linear(in_features=3,out_features=5),
            torch.nn.Sigmoid(),
            torch.nn.Linear(in_features=5, out_features=10),
            torch.nn.Sigmoid(),
            torch.nn.Linear(in_features=10,out_features=5),
            torch.nn.Sigmoid(),
            torch.nn.Linear(in_features=5, out_features=1),
            torch.nn.ReLU(),
        )

    def forward(self,x):
        return self.layers(x)

linear = Linear()

opt = torch.optim.Adam(linear.parameters(),lr= 0.005)
loss = torch.nn.MSELoss()


for epoch in range(3000):
    l = 0
    L2 = 0
    for iter in range(10):

        for w in linear.parameters():
            L2 = torch.norm(w, p=2)*1e8  #计算权重的L2范数，如果要取消L2正则化惩罚只要把这项*0就可以了
        opt.zero_grad()
        output = linear(x_train[iter])
        loss_L2 = loss(output, y_train[iter]) + L2
        loss_L2.backward()
        l = loss_L2.detach() + l
        opt.step()
    print(epoch,L2,loss_L2)

#     plt.scatter(epoch, l, s=5,c='g')
#
# plt.show()


if __name__ == '__main__':
    predict_loss = 0
    for i in range(1000):
        x = torch.tensor([i/100], dtype=torch.float32)
        y_predict = linear(x)
        plt.scatter(x.detach().numpy(),y_predict.detach().numpy(),s=2,c='b')
        plt.scatter(i/100,i*i/10000,s=2,c='y')
        predict_loss = (i*i/10000 - y_predict)**2/(y_predict)**2 + predict_loss   #计算神经元网络模型输出对解析解的loss
# plt.show()

# print(linear.state_dict())
print(predict_loss)

本文的主要参考文献：
[1]Aston Zhang, Mu Li. Dive into deep learning.北京：人民邮电出版社.2021-8