文章目录
- 一、空间复杂度讲解
- 二、计算下列经典例题的空间复杂度
- 1.冒泡排序的空间复杂度 O(1)
- 2.斐波那契递归的空间复杂度 O(N)
- 3.计算阶乘递归的空间复杂度 O(N)
- 三、时间复杂度和空间复杂度的对比
- 四、常见的函数的时间复杂度和空间复杂度的总结
一、空间复杂度讲解
1.空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用额外的存储空间大小的量度
2.空间复杂度算的是变量的个数
3.函数运行时所需要的栈空间(存储参数,局部变量,一些寄存器信息等)在编译期间就已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定(栈帧里面保存的寄存器,形参都可算进空间复杂度,都算常数个)
二、计算下列经典例题的空间复杂度
1.冒泡排序的空间复杂度 O(1)
// 计算BubbleSort的空间复杂度?O(1)
void BubbleSort(int* a, int n)
{//a指向一个数组
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
解析:
注意:用到数组,数组有n个空间,不算冒泡排序的消耗,并不是因为排序而开辟的空间,是本来就有,排序对数组的n个空间进行处理
函数里面开辟的空间end,exchange都是常数个,所以空间复杂度是O(1)
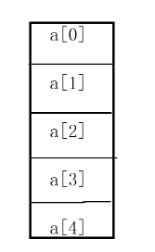
2.斐波那契递归的空间复杂度 O(N)
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}
解析:
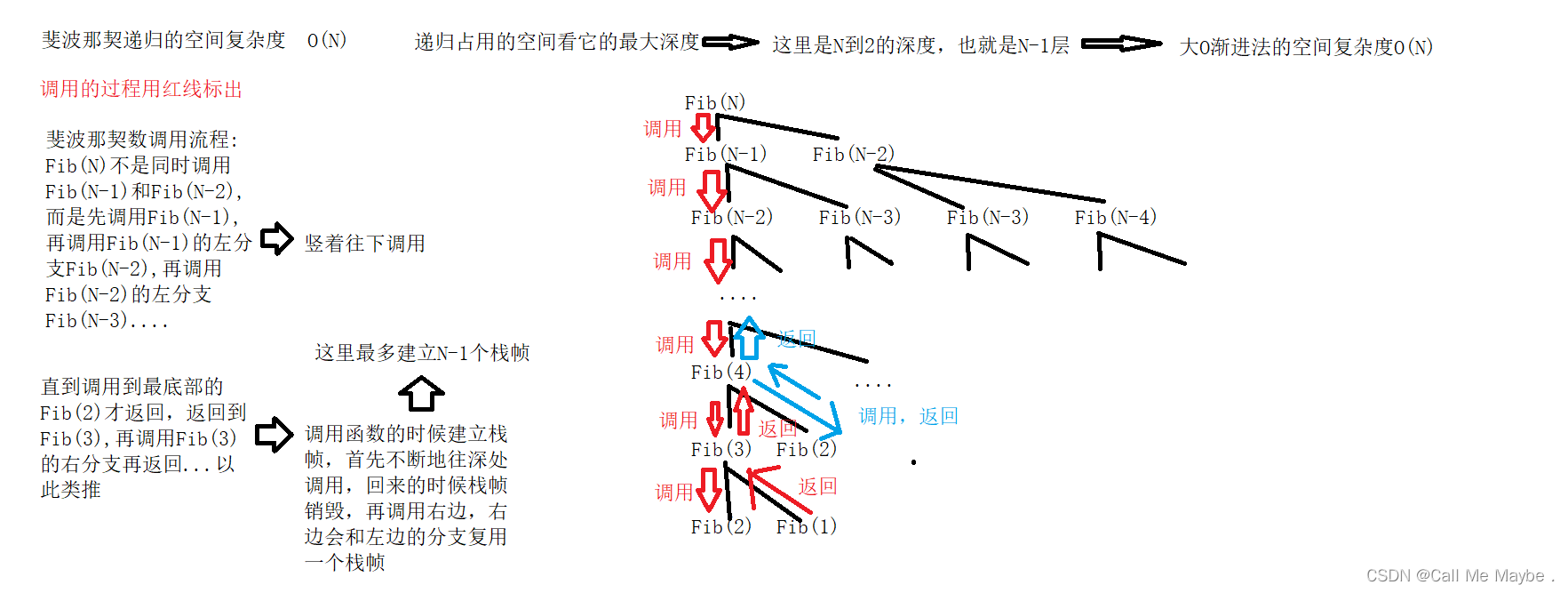
关于上面解析中提到的 栈帧销毁后,再调用函数,会复用栈帧的解释如下:
(1)问题:销毁了栈帧还怎么能够复用?
空间的销毁,栈帧的销毁,变量的销毁,malloc之后的free,他们都不是指把空间整没了,而是归还这块空间的使用权。
(2) 内存空间属于操作系统的进程,而调用函数建立栈帧,或者malloc都是去对应的区域申请空间的使用权。
销毁指的是将这块空间的使用权还给进程,而这块空间还可以给别人用
(3)之所以会复用,首先是因为栈帧是向下建立的,上面是高地址,下面是低地址,而堆是向上生长的,malloc的空间就在堆。
结合本题解释: 调用该函数的时候建立栈帧,调用完毕销毁该栈帧,也就是归还使用权,在此之后紧接着调用函数,又建立栈帧,由于栈帧是向下建立的,所以申请的空间还是刚刚使用过并归还的那块空间,也就是说这个栈帧的重复使用。
注意:在堆上两次malloc分配的空间的地址可能是不一样的
关于堆;
1.堆被称为"向上生长"是指在内存地址空间中,堆的分配方向是从低地址向高地址逐渐增长的。这意味着,随着堆中内存块的分配,新分配的内存块通常会位于已分配内存块的上方。
2.在一般情况下,如果连续多次调用malloc分配内存块,这些内存块的起始地址通常是递增的,即后续分配的内存块的地址比前面分配的内存块的地址要大。
当使用连续的malloc调用时,堆管理器会在堆内存中寻找足够的空闲空间来满足每个分配请求。由于管理机制和内存对齐的考虑,以及其他可能的因素(如堆的碎片化),每次分配的起始地址可能会有所不同。这意味着在实际情况下,即使连续调用多次malloc,返回的内存块的起始地址也可能不同。
因此,一般情况下,连续的malloc调用返回的内存块起始地址有可能不同,但是它们通常是递增的。这是由于堆管理器的分配机制和内存对齐的要求所决定的
(4)进程—(类比)—>酒店
申请内存–> 开房
销毁内存–> 退房
越界 --> 开了一个房间,但通过一些手段比如挖洞还进入了另一个房间
野指针 --> 开房自己偷偷配置了钥匙,再把房卡退了之后,拿着自己配的钥匙去把 房间打开住进去不是你的房间,这时报警相当于系统崩溃
(5)进程地址空间分几个区域:
栈 (局部变量)
堆 (malloc的空间)
静态区 (全局数据和静态数据)
常量区 (常量)
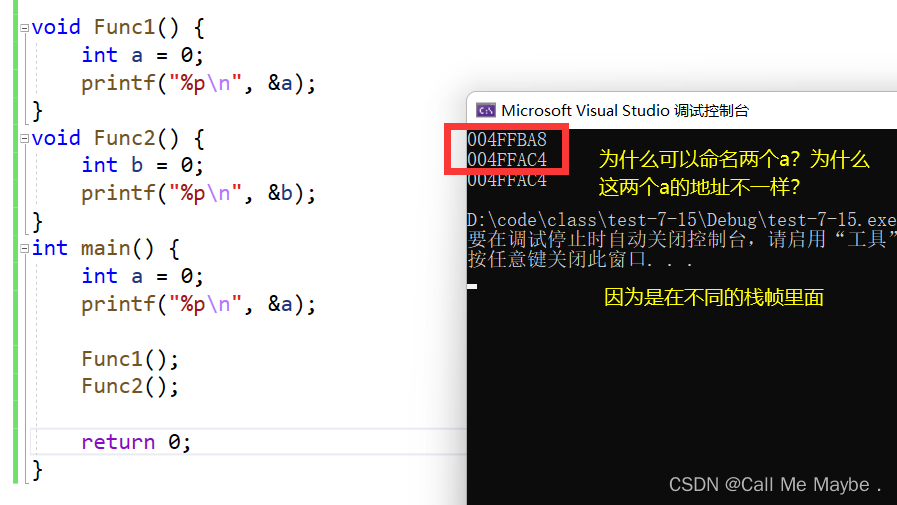
(6)
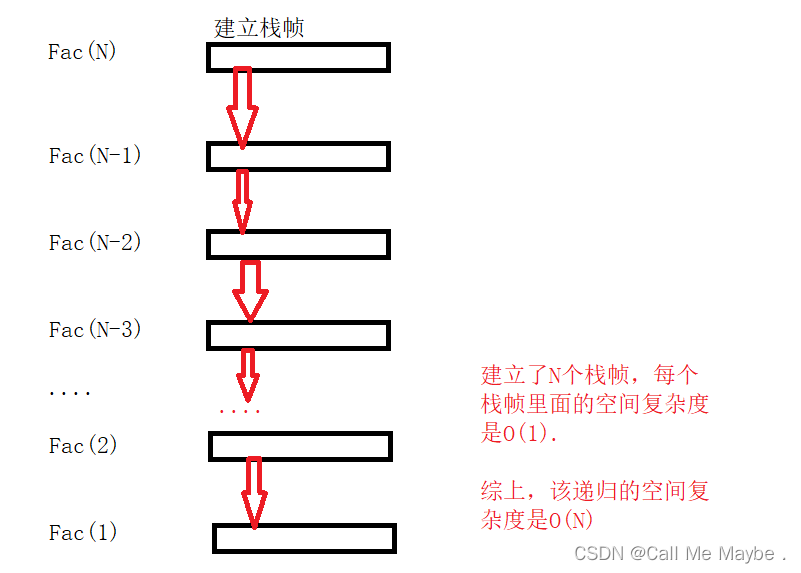
3.计算阶乘递归的空间复杂度 O(N)
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}
递归调用了N次,开辟了N个栈帧,每个栈帧里没有开辟额外的空间,每个栈帧里都是常数个空间
三、时间复杂度和空间复杂度的对比
时间一去不复返,时间是累积计算的、
空间是可以重复利用的,不累积计算
四、常见的函数的时间复杂度和空间复杂度的总结
冒泡排序 时间复杂度 O(N^2) 空间复杂度O(1)
斐波那契递归 时间复杂度 O(2^N) 空间复杂度O(N)
二分查找 时间复杂度 O( log2(N) )
阶乘递归 时间复杂度 O(N) 空间复杂度O(N)