A - Median?A - Median?

题目大意

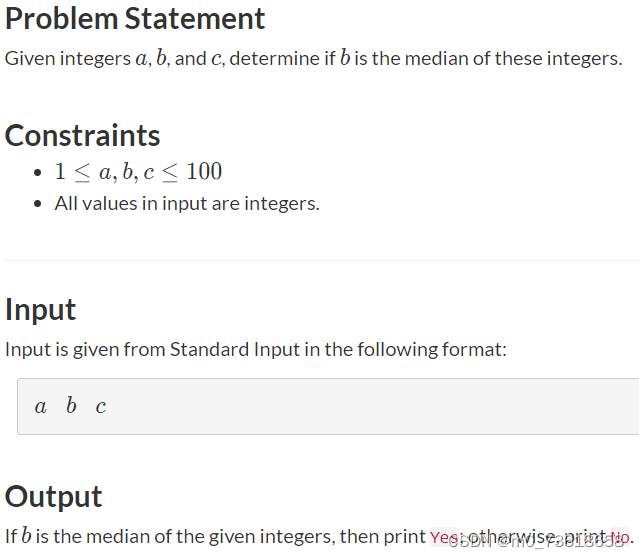
给定三个整数a、b和c，判断b是否是这些整数的中位数。

思路分析

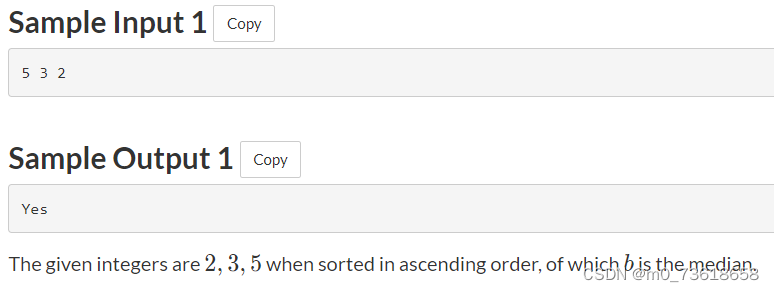
判断升序降序两种情况

时间复杂度分析

O(1)

代码

#include<iostream>
using namespace std;
int main()
{
int a,b,c;
cin>>a>>b>>c;
if((b>=a&&c>=b)||(a>=b&&b>=c))
cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}

B - Distance Between TokensB - Distance Between Tokens

题目大意

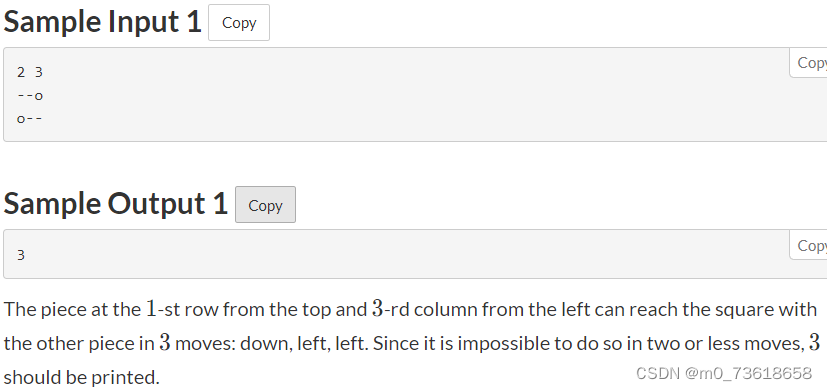
给定一个网格，其中有两个不同的方块上面有棋子。方块的状态由H行W列的字符串S1, …, SH表示。如果S_i,j = ‘o’，表示第i行第j列的方块上有一个棋子；如果S_i,j= ‘-’，表示该方块上没有棋子。允许将其中一个棋子移动到其四周相邻的方块中，但不能移动到网格外部。求使得两个棋子相遇所需的最小移动次数。

思路分析

先找出两个棋子的位置，然后计算它们之间的水平和垂直距离，将两者相加即可得到最小移动次数。

时间复杂度分析

O(H * W)
遍历网格需要O(H * W)的时间复杂度，计算最小移动次数只需常数时间。因此，整体的时间复杂度为O(H * W)。

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 105;

int main() {
    int h, w;
    cin >> h >> w;
    char a[N][N];
    vector<pair<int, int>> b;
    
    for(int i = 0; i < h; i++) {
        for(int j = 0; j < w; j++) {
            cin >> a[i][j];
            if(a[i][j] == 'o') {
                b.push_back({i, j});
            }
        }
    }
    
    cout << abs(b[0].first - b[1].first) + abs(b[0].second - b[1].second) << endl;

    return 0;
}

C - Max - Min QueryC - Max - Min Query

题目大意

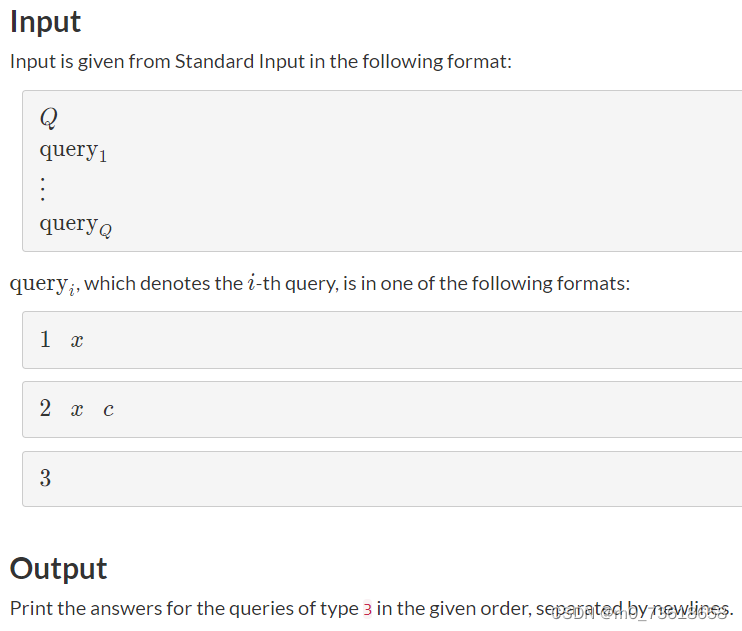
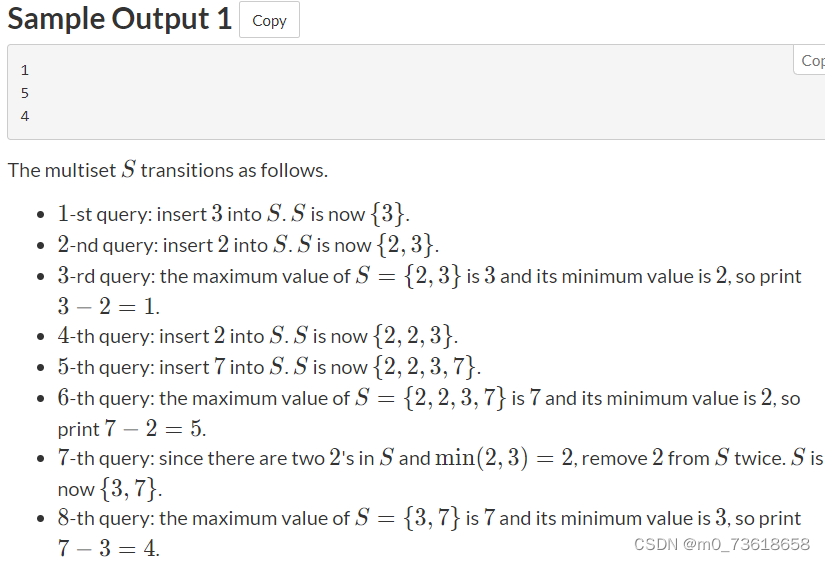
题目要求处理一系列的查询操作。

查询1，将一个整数插入到数列S中；
查询2，计算数列中移除指定整数的最多c个元素(不超过数列有指定整数的个数)；
查询3，计算multiset中最大值和最小值之间的差值。

思路分析

首先，我们声明一个空的multiset容器 multiset st; ，用于存储整数元素。

然后，使用循环处理所有的查询。在每个查询中，根据不同的操作类型执行相应的操作：

对于查询1，读取整数x，并使用 st.insert(x) 将x插入到multiset中。
对于查询2，读取整数x和次数c。通过循环 while (c-- and st.find(x) != st.end()) ，删除multiset中最多c个等于x的元素。
对于查询3，在multiset中找到最大值和最小值，计算并输出它们的差值 *st.rbegin() - *st.begin() 。

知识点积累

std::multiset<int> st;

1.erase() 当集合st包含{3, 3, 4}时，执行下面的代码会发生什么？

st.erase(3);

我们期望只删除一个3，但实际上st的内容变成了{4}。如果将一个值作为erase()的参数，它将删除所有具有该值的元素，因此需要小心处理。

如果要删除单独的x，应该这样编写代码：

st.erase(st.find(x));

2.count()的复杂度使用st.count(x)的计算时间为O(k + log N)，其中N是st中元素的数量，k是st中包含x的数量。

因此，如果在处理查询2时使用st.count(x)，最坏情况下总共需要O(Q^2)的时间。相反，你应该使用O(log N)的操作，它的时间复杂度为O(log N)。由于st.find(x)最多被调用O(Q)次，这样可以适应时间限制。

时间复杂度分析

O(Q^2 log N^)

代码

#include <bits/stdc++.h>
using namespace std;

int main() {
    int q;
    cin >> q;
    multiset<int> st;
    while (q--) {
        int t;
        cin >> t;
        if (t == 1) {
            int x;
            cin >> x;
            st.insert(x);
        } else if (t == 2) {
            int x, c;
            cin >> x >> c;
            while (c-- and st.find(x) != st.end()) {
                st.erase(st.find(x));
            }//c-- 表示每次循环时将c的值减1，并检查结果是否为非零。当c的值降至0时，循环将停止。
            //st.find(x) 用于查找multiset st 中第一个等于x的元素的迭代器。
        } 
        else {
            cout << *st.rbegin() - *st.begin() << endl;//st.begin() 返回multiset st 中第一个（最小的）元素的迭代器。
            //st.rbegin() 返回multiset st 中最后一个（最大的）元素的反向迭代器。
        }
    }
}