594. 最长和谐子序列（简单）

方法：哈希表计数

思路

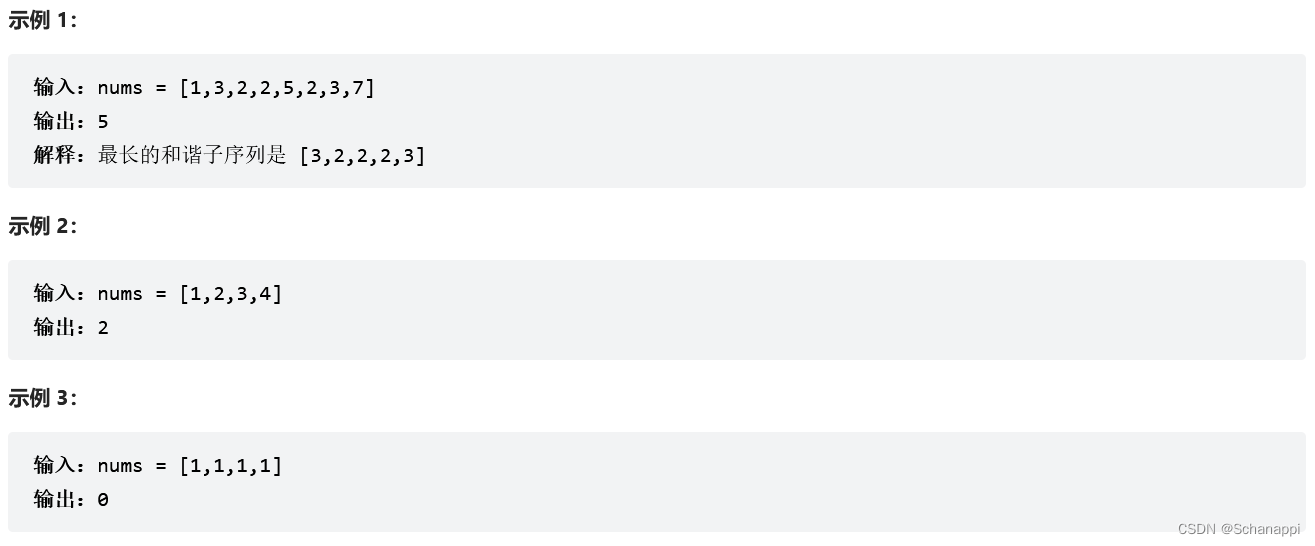
• 题目规定的「和谐子序列」中的最值差值正好为 1，因而子序列排序后必然符合[a,a,.., a +1,a+1]形式，即符合条件的和谐子序列长度为相邻两数(差值为 1)的出现次数之和。
• 因此，我们首先对 nums 各元素的出现次数计数，之后再次遍历，如果存在比该元素小 1 的元素，说明这两个元素会形成和谐子序列，此时将二者的出现次数相加，即为可能的答案之一。
• 最后，将最佳答案与可能答案相比较，较大者更新为最佳答案。

代码

class Solution {
public:
    int findLHS(vector<int>& nums) {
        unordered_map<int, int> mp;
        int ans = 0;
        for (int n : nums){
            if(mp.find(n) == mp.end()){
                mp.insert({n, 1});
            }
            else mp[n]++;
        }
        for(auto m : mp){
            if(mp.find(m.first - 1) != mp.end()){
                ans = max(ans, m.second + mp[m.first - 1]);
            }
        }
        return ans;
    }
};