A - You should output ARC, though this is ABC.A - You should output ARC, though this is ABC.
题目大意
给定整数R和C以及一个2x2矩阵A,需要输出A R,C的值。
思路分析
简单的矩阵查找。根据给定的索引R和C,找到矩阵A中相应位置的元素,并输出它的值。
这题用数组更好。
时间复杂度
O(1)
代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int m,n;
cin>>m>>n;
vector<vector<int>> a(2,vector<int>(2));
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
cin>>a[i][j];
}
}
cout<<a[m-1][n-1]<<endl;
return 0;
}
B - Light It UpB - Light It Up
题目大意
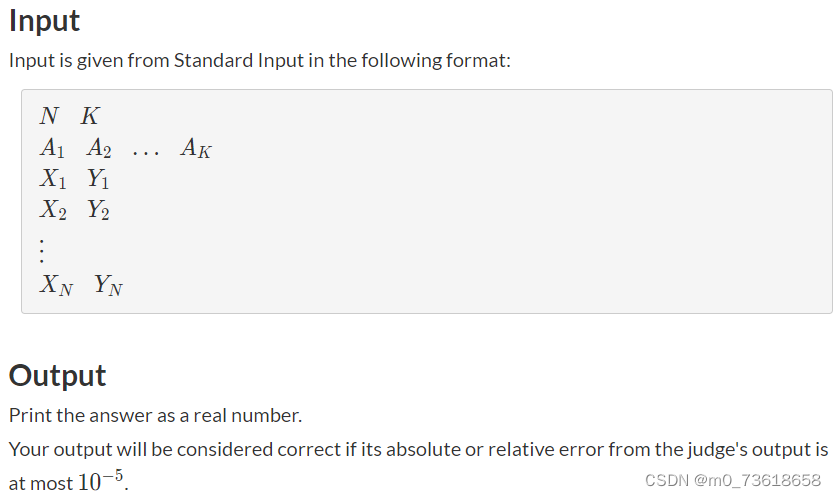
在二维平面上有N个人,编号为1, 2, …, N。每个人的坐标分别为(Xi, Yi)。
其中的K个人,即A1, A2, …, AK,将接收到相同强度的光。(这k个人有光)
当位于坐标(x, y)处的人拥有强度为R的光时,它会照亮以(x, y)为中心、半径为R的圆内部(包括边界)的区域。
要求找出使得每个人至少被一盏灯照亮所需的最小光强度。
思路分析
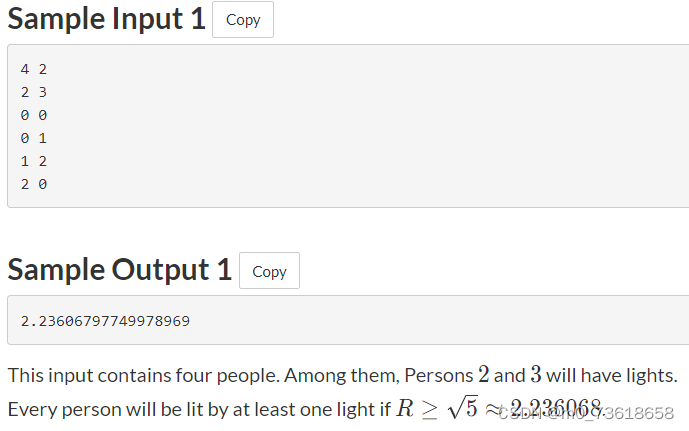
为了确保每个人至少被一盏灯照亮,我们需要找到每个人到最近(min)的具有灯的人之间的距离,并找到在所有人中每个人到最近(min)的具有灯的人之间的距离的最大值(max)作为光的强度。
实际上,只有当“对于每个人,存在至少一个距离不超过R的人”时才成立。
这可以进一步重新表述为:“如果D≤R,则一个人被一盏灯照亮”,其中D是该人与最近的具有光的人之间的距离。
因此,问题的答案是每个人到最近的“有光的人”的最大距离,可以通过双重循环在O(NK)时间内找到。
时间复杂度
O(NK)
代码
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,k;k
cin >> n >> k;
vector<int> a(k); // 存储接收光的人的编号
for(auto &nx : a){
cin >> nx;
nx--; // 让编号从0开始
}
vector<long long> x(n),y(n);
for(int i=0;i<n;i++){cin >> x[i] >> y[i];}
long long res=0;
for(int i=0;i<n;i++){
long long cres=8e18; // 初始化最近距离为一个很大的数
for(auto &nx : a){
cres=min(cres,(x[i]-x[nx])*(x[i]-x[nx]) + (y[i]-y[nx])*(y[i]-y[nx])); // 计算与当前人之间的距离的平方
}
res=max(res,cres); // 取最大距离作为光的强度
}
printf("%.12lf\n",sqrt((double)res)); // 输出最小光强度,保留12位小数
return 0;
}
C - ±1 Operation 1C - ±1 Operation 1
题目大意
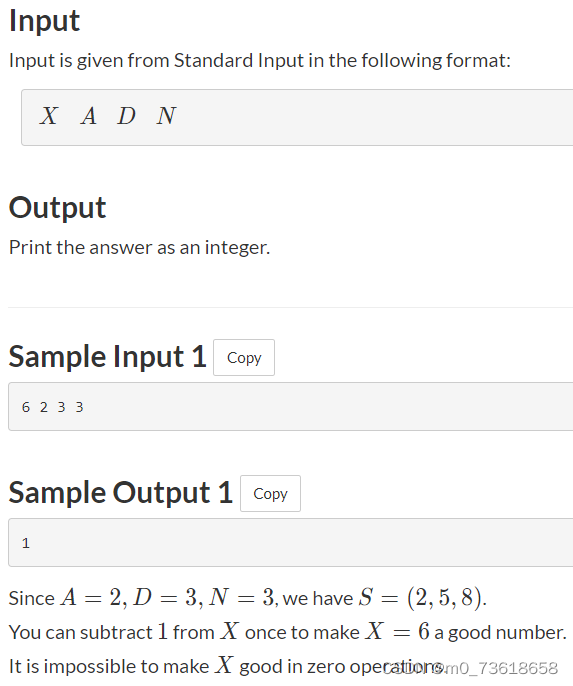
将给定的整数X转化为等差数列S中的一个好数字(good number),即满足初始项为A,公差为D,长度为N的等差数列S中的某一项。操作可以选择加1或减1。
思路分析
通过判断X与等差数列S的最小值st和最大值fi的关系来确定需要进行的操作次数。
- 如果st <= X <= fi,则X在等差数列范围内,可以计算X与st之间的差m,然后取m和D-m的较小值作为答案。这里使用了取模运算%。
- 如果X < st,则需要将X增加到st,操作次数为st-X。
- 如果X > fi,则需要将X减少到fi,操作次数为X-fi。
笔记
如果有正有负两种情况。把负数转换成正数,进行处理。
本题中,由于D < 0比较困难处理,所以进行规范化操作,使得D >= 0:
同时替换A=A+D * (N-1)和D=-D。
这相当于对等差数列进行反转。例如,如果A=8,D=-3,N=3,则序列S=(8,5,2),但是通过将A=2,D=3,N=3进行替换,我们得到S=(8,5,2),与之前的序列相反,而“好数字”的集合保持不变。
时间复杂度
O(1)
代码
#include<bits/stdc++.h>
using namespace std;
int main(){
long long x,a,d,n;
cin >> x >> a >> d >> n;
if(d<0){
long long fi=a+d*(n-1);
a=fi;
d*=-1;
}
long long st=a;
long long fi=a+d*(n-1);
if(st<=x && x<=fi){
long long m;
if(d!=0){m=(x-st)%d;}
else{m=0;}
cout << min(m,d-m) << '\n';
}
else if(x<st){cout << st-x << '\n';}
else{cout << x-fi << '\n';}
return 0;
}