问题描述

给定一个长度为 n 的整数数组 height 。有n条垂线，第i条线的两个端点是(i, 0)和(i, height[i])。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。

示例1

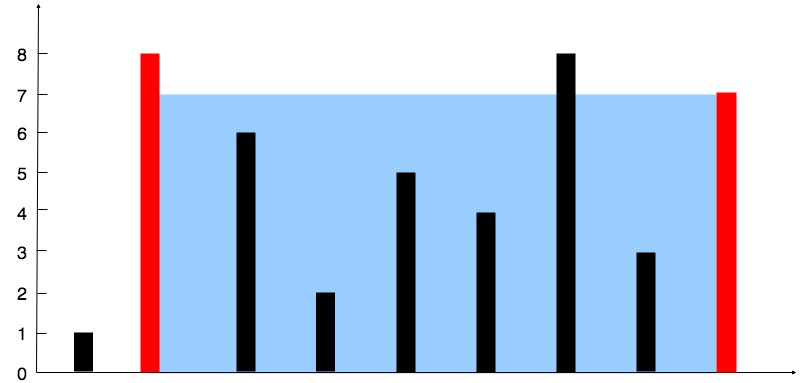
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例2

输入：height = [1,1]
输出：1

提示

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

思路分析

1. 首先，我们定义了一个Solution类，其中包含解决问题的方法maxArea。
2. 方法maxArea接收一个整数数组height作为参数。
3. 我们通过双指针来解决这个问题。左指针left初始化为数组的第一个元素下标0，右指针right初始化为数组最后一个元素的下标n-1。
4. 初始化最大面积max_area为0。
5. 进入循环，条件是左指针小于右指针。这是因为当左指针和右指针相遇时，无法再构成有效的容器。
6. 在每一次循环中，我们计算当前的面积curr_area。面积的计算公式是两个指针所指高度较小值乘以两个指针之间的距离即(right - left)。
7. 更新最大面积max_area，通过将当前面积curr_area与max_area比较，如果curr_area更大，则更新max_area。
8. 接下来，根据以下三种情况移动指针：
   • 如果height[left]小于height[right]，那么我们将左指针left向右移动一位，即left += 1，因为移动左指针不能增加当前的面积。
   • 如果height[left]大于height[right]，那么我们将右指针right向左移动一位，即right -= 1，因为移动右指针不能增加当前的面积。
   • 如果height[left]等于height[right]，那么我们既可以移动左指针也可以移动右指针。在这种情况下，无论移动哪个指针，都不会改变当前的面积。
9. 循环结束后，返回最大面积max_area作为结果。

这种解决方法的核心思想是通过不断缩小有效宽度的范围，来寻找容器的最大面积。通过比较较小高度的指针向内移动，可以保留更有可能得到更大面积的高度。最终，我们得到了两条垂线所形成容器的最大面积。

代码分析

1. 首先，我们定义了一个Solution类。
2. 在类中，我们定义了一个方法maxArea，它接收一个整数数组height作为参数。
3. 我们首先获取数组height的长度n，用于后续循环的条件判断。
4. 初始化左指针left为0，右指针right为数组最后一个元素的下标n-1。
5. 初始化最大面积max_area为0。
6. 进入循环，条件是左指针left小于右指针right。
7. 在循环中，我们计算当前的面积curr_area，即两个指针所指高度较小值乘以两个指针之间的距离，使用min()函数取得较小值。
8. 更新最大面积max_area，通过将当前面积curr_area与max_area比较，并将较大值赋给max_area，用max()函数实现。
9. 接下来，使用三个判断条件来决定指针的移动：
   • 如果height[left]小于height[right]，说明左指针指向的高度较低，移动左指针left向右移动一位，即left += 1。
   • 如果height[left]大于height[right]，说明右指针指向的高度较低，移动右指针right向左移动一位，即right -= 1。
   • 如果height[left]等于height[right]，说明两边的高度相等，无论左指针left还是右指针right都可以移动，所以同时将左指针left向右移动一位，即left += 1，右指针right向左移动一位，即right -= 1。
10. 循环结束后，返回最大面积max_area作为结果。

完整代码

class Solution(object):
    def maxArea(self, height):
        n = len(height)  # 获取数组height的长度n
        left, right = 0, n - 1  # 初始化左指针left为0，右指针right为数组最后一个元素的下标n-1
        max_area = 0  # 初始化最大面积max_area为0

        while left < right:  # 进入循环，条件是左指针left小于右指针right
            curr_area = min(height[left], height[right]) * (right - left)  # 计算当前的面积curr_area，即两个指针所指高度较小值乘以两个指针之间的距离
            max_area = max(max_area, curr_area)  # 更新最大面积max_area，通过将当前面积curr_area与max_area比较，并将较大值赋给max_area

            if height[left] < height[right]:  # 如果height[left]小于height[right]
                left += 1  # 移动左指针left向右移动一位
            elif height[left] > height[right]:  # 如果height[left]大于height[right]
                right -= 1  # 移动右指针right向左移动一位
            else:  # 如果height[left]等于height[right]
                left += 1  # 同时移动左指针left向右移动一位
                right -= 1  # 同时移动右指针right向左移动一位
        
        return max_area  # 返回最大面积max_area作为结果

详细分析

1. 首先定义一个名为Solution的类。

class Solution(object):

2. 然后，我们在Solution类中定义了一个名为maxArea的方法，该方法接收一个名为height的参数。

    def maxArea(self, height):

3. 在方法体内部，我们获取数组height的长度，并将结果赋给变量n。

        n = len(height)

4. 接下来，我们初始化左指针left为0，右指针right为数组最后一个元素的下标n-1。

        left, right = 0, n - 1

5. 我们还定义了一个变量max_area，并将其初始化为0，用于保存最大面积的值。

        max_area = 0

6. 在接下来的while循环中，我们判断左指针是否小于右指针，如果是，则执行循环体内的代码。

        while left < right:

7. 在循环体内部，我们首先计算当前的面积curr_area，即两个指针所指高度较小值乘以两个指针之间的距离。

            curr_area = min(height[left], height[right]) * (right - left)

8. 接着，我们更新最大面积max_area，通过将当前面积curr_area与max_area比较，并将较大值赋给max_area。

            max_area = max(max_area, curr_area)

9. 然后，我们根据左指针和右指针指向的高度来移动指针。

• 如果左指针指向的高度小于右指针指向的高度，则将左指针向右移动一位。

            if height[left] < height[right]:
                left += 1

• 如果左指针指向的高度大于右指针指向的高度，则将右指针向左移动一位。

            elif height[left] > height[right]:
                right -= 1

• 如果左指针指向的高度等于右指针指向的高度，则同时将左指针向右移动一位，并将右指针向左移动一位。

            else:
                left += 1
                right -= 1

10. 循环结束后，我们返回最大面积max_area作为结果。

        return max_area

运行效果截图

调用示例

solution = Solution()
x = [1,8,6,2,5,4,8,3,7]
x1 = [1,1]
print(solution.maxArea(x))
print(solution.maxArea(x1))

运行结果

完结