各位CSDN的uu们你们好呀,今天继续数据结构与算法专栏中的二叉树,下面,让我们进入二叉树的世界吧!!!
二叉树(上)——“数据结构与算法”_认真学习的小雅兰.的博客-CSDN博客
二叉树链式结构的实现
二叉树链式结构的实现
求二叉树的高度
//求二叉树的高度 int BTreeHeight(BTNode* root) { if (root == NULL) { return 0; } else { return BTreeHeight(root->left) > BTreeHeight(root->right) ? BTreeHeight(root->left) + 1 : BTreeHeight(root->right) + 1; } }但是这种写法有很大的问题!!!
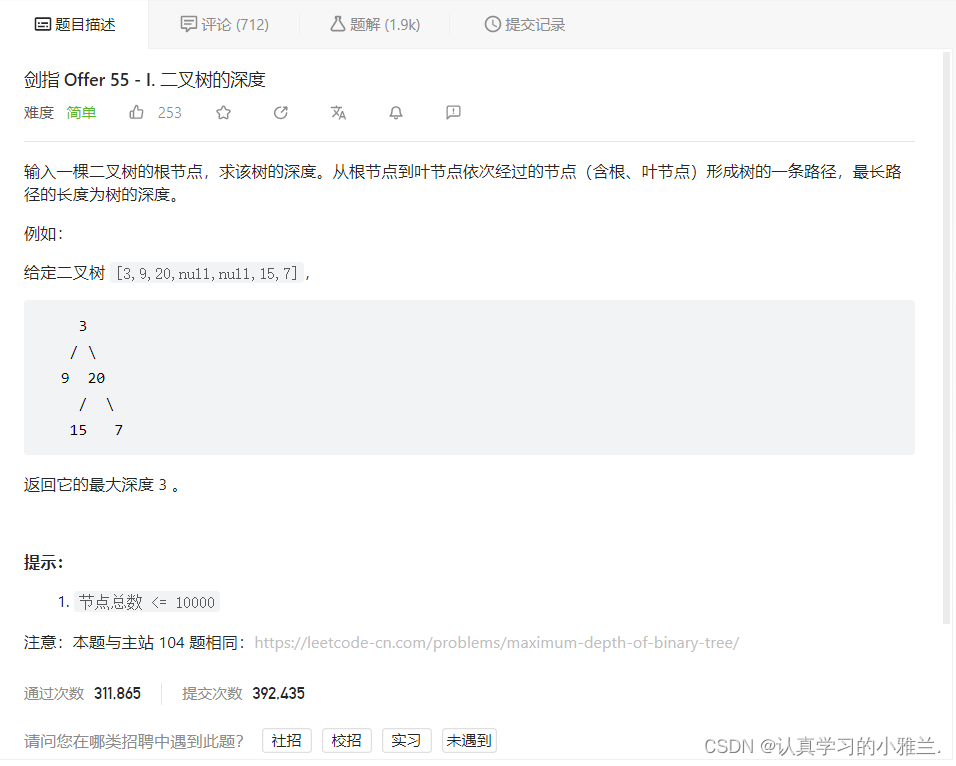
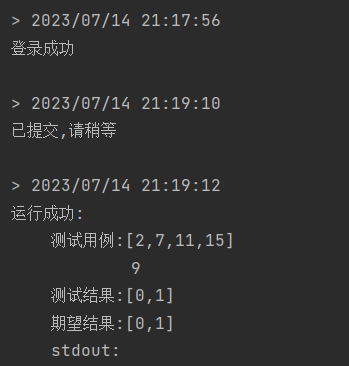
下面,我们来看leetcode上面有一个类似的题目。
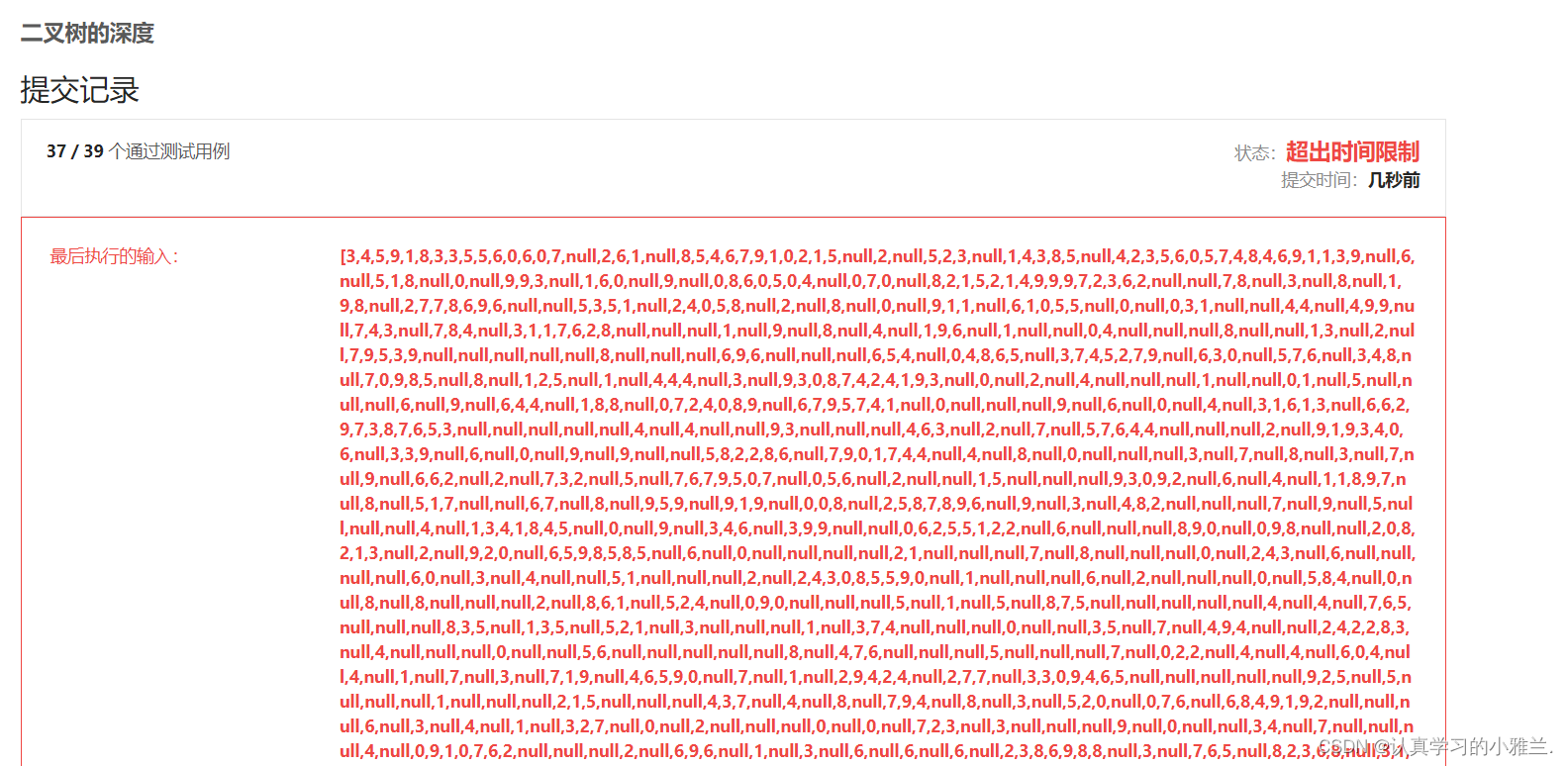
会发现:这种写法是过不了的!!!
当这棵树特别大的时候,leetcode会提示超出时间限制!!!
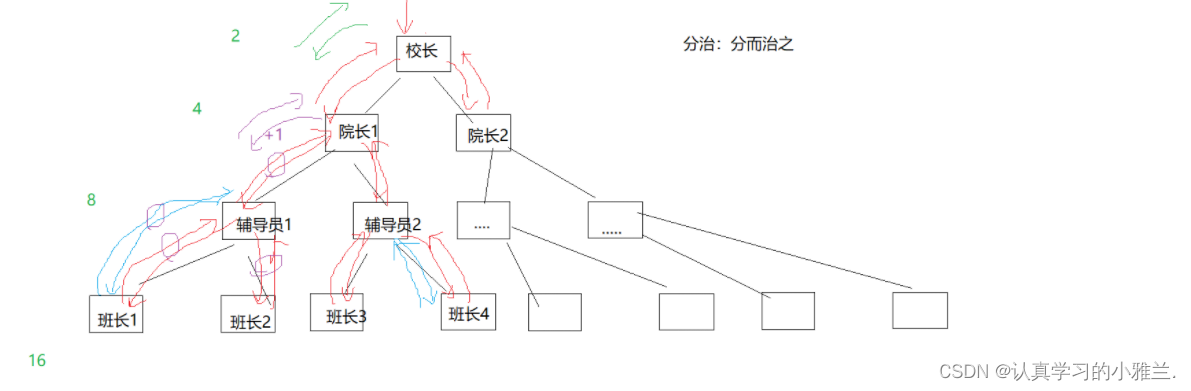
下面,我来举一个生动形象的例子
在这张图上,所有的领导都不记事。校长找院长1,院长1找辅导员1,辅导员1找班长1,班长1返回了一个结果给辅导员1,辅导员1又找班长2,班长2也返回了一个结果给辅导员1,但是这个辅导员1只比较了班长1和班长2所返回的结果谁大谁小,并没有把数据记录下来。等到班长2返回完结果之后,辅导员1又再一次找班长1要数据(班长1的数据比较好),班长1又要再一次返回数据结果。现在,辅导员1终于可以把结果返回给院长1了, 然后,院长1开始找辅导员2,辅导员2找班长3,班长3返回结果给辅导员2,辅导员2找班长4,班长4也返回结果给辅导员2,但是辅导员2仍然只是比较了班长3和班长4所返回的数据结果的大小,并没有把数据记录下来,假设班长4的数据比较好,也就是:班长4刚刚把数据报给辅导员2,回到宿舍,辅导员紧接着打了个电话给班长4,要他来汇报数据。现在辅导员2终于把数据汇报给院长1了,但是,这个院长1只比较了辅导员1和辅导员2所返回的数据结果的大小,还是没有记录数据。假设辅导员1的数据比较好,辅导员1又得找两个班长重复上面的过程(关键是辅导员1不记事,再一次比较了班长1和班长2的数据后,又得把班长1叫过去汇报数据)(班长1:我真是栓Q,没完没了了是吧)
这样是非常恐怖的!!!
调用的次数成等比数列(成倍地增加,每一层都是一个叠加的double)
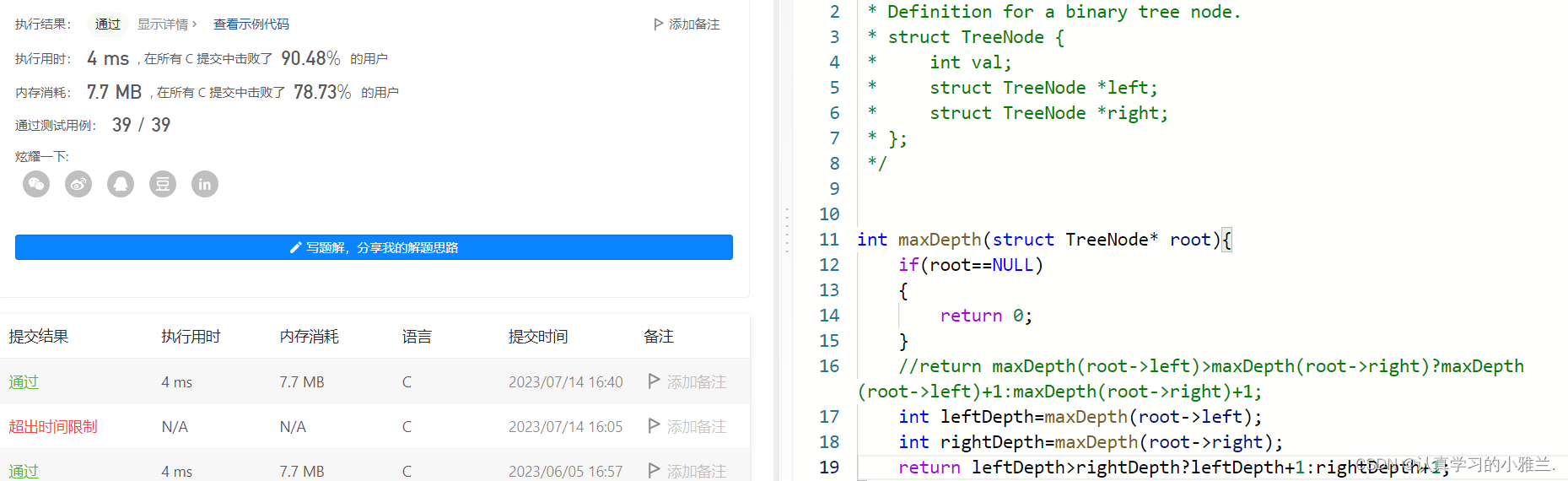
所以,这个题目的最优解是:
int maxDepth(struct TreeNode* root) { if(root==NULL) { return 0; } int leftDepth=maxDepth(root->left); int rightDepth=maxDepth(root->right); return leftDepth>rightDepth?leftDepth+1:rightDepth+1; }
所以求二叉树的高度的源代码:
//求二叉树的高度 int BTreeHeight(BTNode* root) { if (root == NULL) { return 0; } else { int leftHeight = BTreeHeight(root->left); int rightHeight = BTreeHeight(root->right); return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1; } }
二叉树第k层结点个数
子问题:转换成左子树的第k-1层和右子树的第k-1层
结束条件:k==1且结点不为空
// 二叉树第k层节点个数 int BTreeLevelKSize(BTNode* root, int k) { assert(k > 0); if (root == NULL)//无论k是多少 { return 0; } //root一定不为空 if (k == 1) { return 1; } //root不为空并且k不为1 return BTreeLevelKSize(root->left, k - 1) + BTreeLevelKSize(root->right, k - 1); }
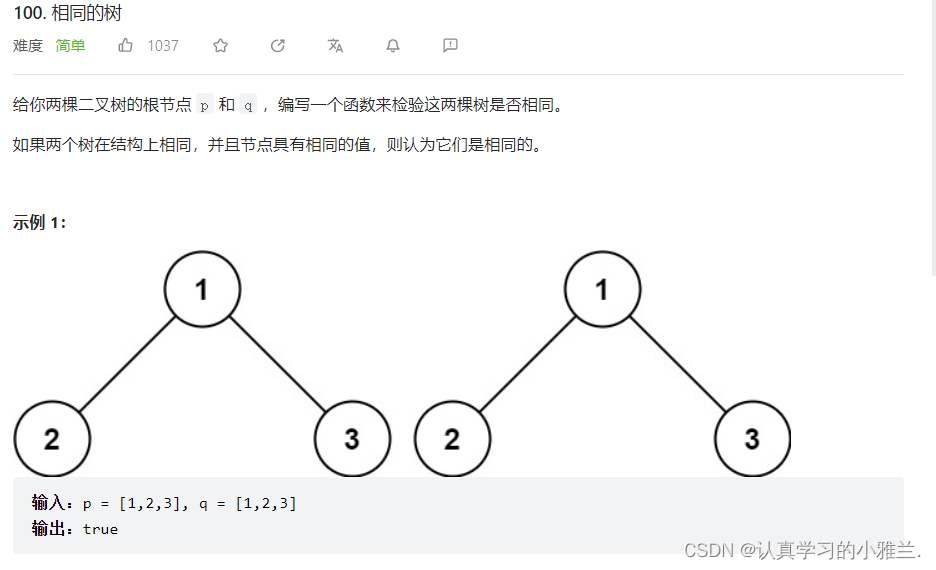
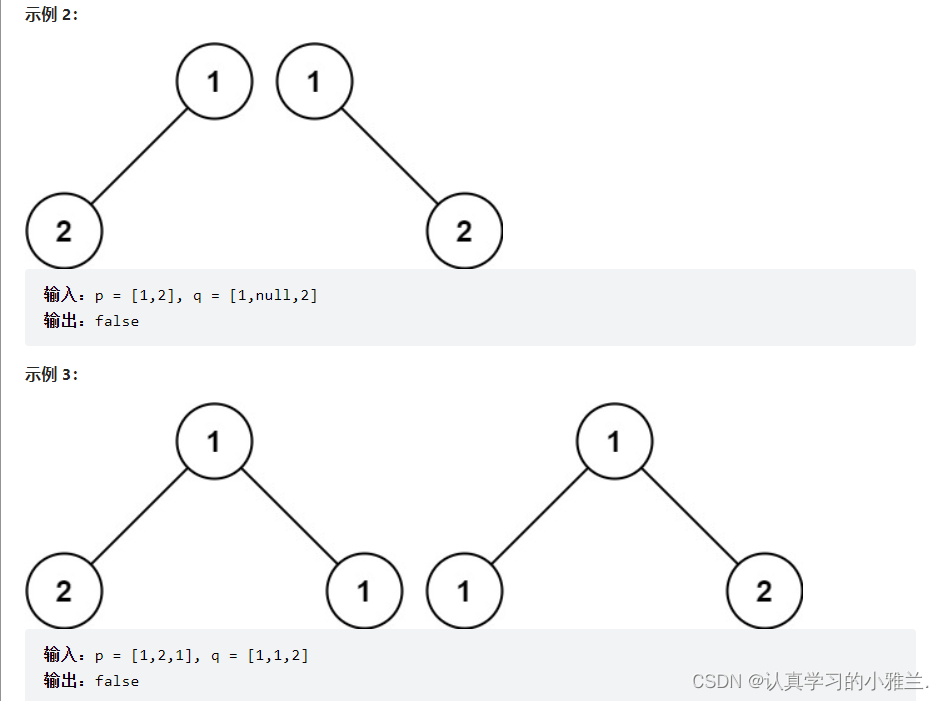

使用前序比较!!!
二叉树里面不敢轻易使用断言(因为二叉树里面有NULL)
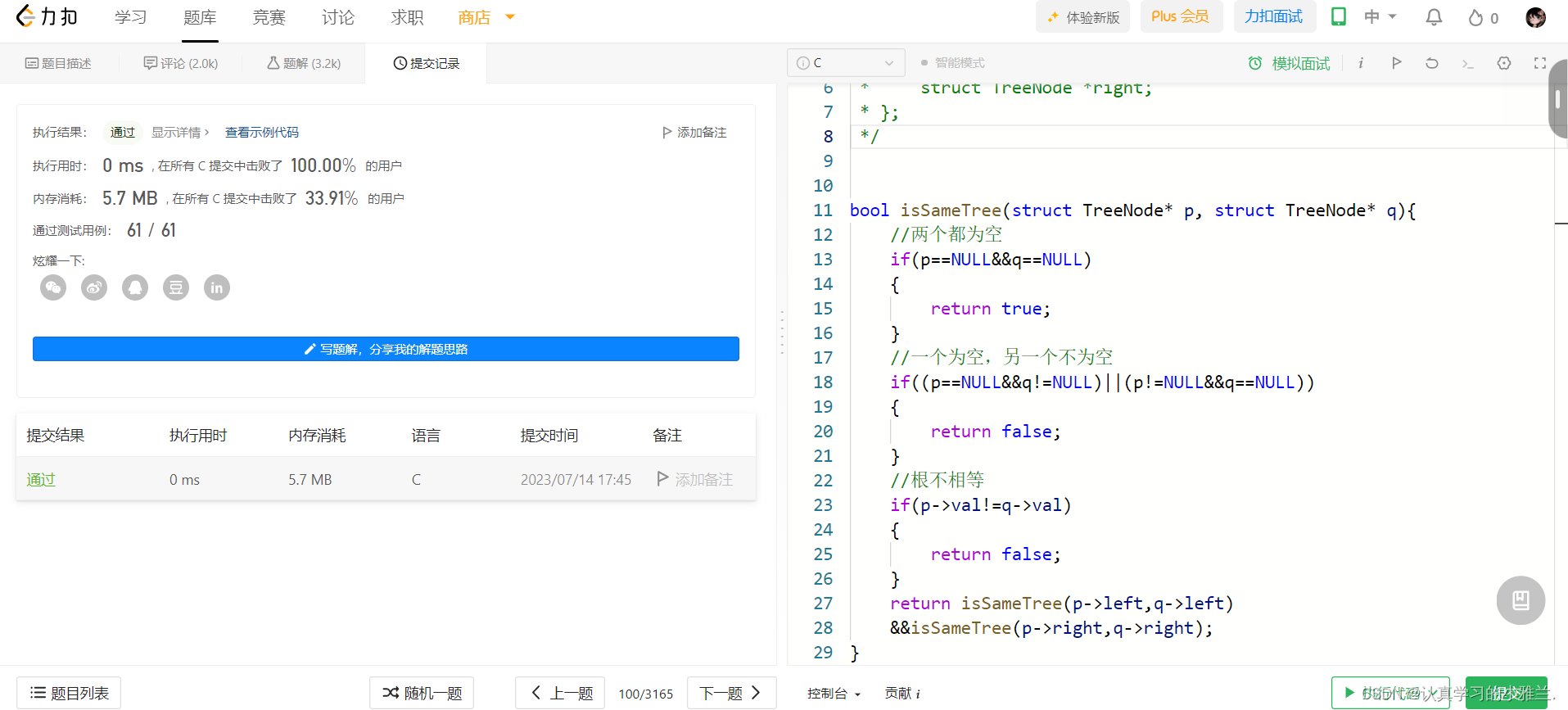
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//两个都为空
if(p==NULL&&q==NULL)
{
return true;
}
//一个为空,另一个不为空
if((p==NULL&&q!=NULL)||(p!=NULL&&q==NULL))
{
return false;
}
//根不相等
if(p->val!=q->val)
{
return false;
}
return isSameTree(p->left,q->left)
&&isSameTree(p->right,q->right);
}
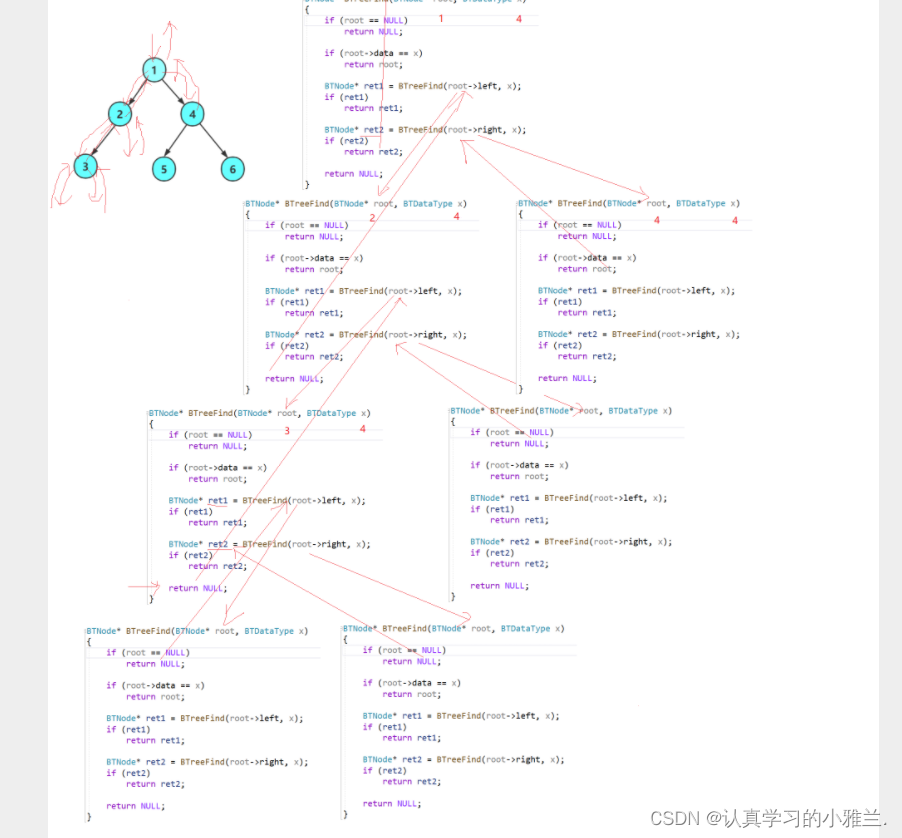
二叉树查找值为x的结点
使用前序查找!!! 根 左子树 右子树
// 二叉树查找值为x的节点 BTNode* BTreeFind(BTNode* root, BTDataType x) { if (root == NULL) { return NULL; } if (root->data == x) { return root; } BTNode* ret1 = BTreeFind(root->left, x); if (ret1) { return ret1; } BTNode* ret2 = BTreeFind(root->right, x); if (ret2) { return ret2; } return NULL; }

bool isUnivalTree(struct TreeNode* root){
if(root==NULL)
{
return true;
}
if(root->left&&root->left->val!=root->val)
{
return false;
}
if(root->right&&root->right->val!=root->val)
{
return false;
}
return isUnivalTree(root->left)&&
isUnivalTree(root->right);
} 
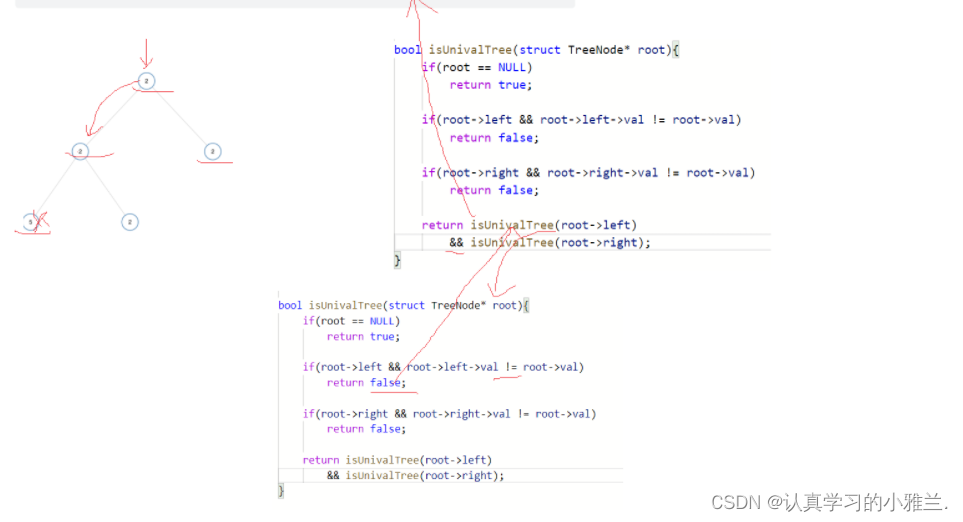
二叉树的源代码如下:
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
//求二叉树的高度
int BTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
else
{
int leftHeight = BTreeHeight(root->left);
int rightHeight = BTreeHeight(root->right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
}
// 二叉树第k层节点个数
int BTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)//无论k是多少
{
return 0;
}
//root一定不为空
if (k == 1)
{
return 1;
}
//root不为空并且k不为1
return BTreeLevelKSize(root->left, k - 1) + BTreeLevelKSize(root->right, k - 1);
}
// 二叉树查找值为x的节点
BTNode* BTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* ret1 = BTreeFind(root->left, x);
if (ret1)
{
return ret1;
}
BTNode* ret2 = BTreeFind(root->right, x);
if (ret2)
{
return ret2;
}
return NULL;
}int main()
{printf("BTreeHeight:%d\n", BTreeHeight(root));
printf("BTreeLevelKSize:%d\n", BTreeLevelKSize(root, 3));
printf("BTreeFind:%p\n", BTreeFind(root, 3));
return 0;
}
好啦,小雅兰今天的内容就到这里啦,还要继续加油呀!!!