文章目录
- 简单知识导入:
- 具体过程:
- 密钥生成
- 代码部分
- 参考
简单知识导入:
DES算法是属于对称密码算法中的分组加算法。
分组加密和流密码加密是相对应的。
流密码是逐字节进行加密,即一个字节一个字节进行加密
分组加密算法也叫块加密,将明文分成固定字节块,对每个字节块分别进行加密,最后拼接在一起得到密文
密钥长64位,56位参与运算,其余8位为校验位。(8,16,24,32,40,48,56,64) 可以看出是8的倍数
当n个64位明文数据块都经过DES加密处理后,所得到的n个64位密文数据块串在一起就是密文。
具体过程:
采用
F
e
i
s
t
e
l
算法
:
采用Feistel算法:
采用Feistel算法:
L
i
=
R
i
−
1
L_i = R_{i-1}
Li=Ri−1
R
i
=
L
i
−
1
⊕
f
(
R
i
−
1
,
K
i
)
R_i = L_{i-1} \oplus f(R_{i-1}, K_i)
Ri=Li−1⊕f(Ri−1,Ki)


首先对 64 b i t s 的明文进行初始 I P 置换,得到打乱顺序的 64 b i t s 的数据 接着对它对半分,得到 32 b i t s 的 L 0 和 R 0 自此开始进入 F e i s t e l 算法,知道 R 就很容易知道 L , 所以要解决就得从 R 入手, 已知 R i = L i − 1 ⊕ f ( R i − 1 , K i ) , f ( ) 即使图中的 F 轮函数,进行完【 4. P 置换】后即可得到 f ( R i − 1 , K i ) 接着将其与 L i − 1 进行异或即可得到 R i , 自此第一轮运算结束, 经过 16 轮相同的运算得到 L 16 和 R 16 , 拼接在一起后进行最后的逆初始置换即可得到最终的密文 首先对64bits的明文进行初始IP置换,得到打乱顺序的64bits的数据\\接着对它对半分,得到32bits的L_{0}和R_{0}\\自此开始进入Feistel算法,知道R就很容易知道L,所以要解决就得从R入手,\\ 已知R_i = L_{i-1} \oplus f(R_{i-1}, K_i),\\f()即使图中的F轮函数,进行完【4.P置换】后即可得到f(R_{i-1}, K_i)\\ 接着将其与L_{i-1}进行异或即可得到R_{i},自此第一轮运算结束,\\经过16轮相同的运算得到L_{16}和R_{16},\\拼接在一起后进行最后的逆初始置换即可得到最终的密文 首先对64bits的明文进行初始IP置换,得到打乱顺序的64bits的数据接着对它对半分,得到32bits的L0和R0自此开始进入Feistel算法,知道R就很容易知道L,所以要解决就得从R入手,已知Ri=Li−1⊕f(Ri−1,Ki),f()即使图中的F轮函数,进行完【4.P置换】后即可得到f(Ri−1,Ki)接着将其与Li−1进行异或即可得到Ri,自此第一轮运算结束,经过16轮相同的运算得到L16和R16,拼接在一起后进行最后的逆初始置换即可得到最终的密文
下面我们对照图中一个一个来讲解
IP置换( 64 − > 64 64->64 64−>64)
按照一定的规则,将原来的
64
比特的二进制数进行重新排序,
这里的规则即指初始置换表(最后的
I
P
逆置换和此处置换过程一模一样,仅表不同),
对照下面的表,将二进制明文的第
58
位放到第一位,
第
50
位放到第二位,以此类推,最终得到重新排序的数据。自此,
I
P
置换完成。
按照一定的规则,将原来的64比特的二进制数进行重新排序,\\这里的规则即指初始置换表(最后的IP逆置换和此处置换过程一模一样,仅表不同),\\ 对照下面的表,将二进制明文的第58位放到第一位,\\第50位放到第二位,以此类推,最终得到重新排序的数据。自此,IP置换完成。
按照一定的规则,将原来的64比特的二进制数进行重新排序,这里的规则即指初始置换表(最后的IP逆置换和此处置换过程一模一样,仅表不同),对照下面的表,将二进制明文的第58位放到第一位,第50位放到第二位,以此类推,最终得到重新排序的数据。自此,IP置换完成。

轮函数–E扩展置换( 32 − > 48 32->48 32−>48)
我觉得这里对照下面的图看是能看懂的,先将
32
b
i
t
s
的
R
分成
8
组,每组
4
b
i
t
s
,
每组最前和最后各加
1
b
i
t
s
,
不是随便加,按图中所给的表进行扩展
我觉得这里对照下面的图看是能看懂的,先将32bits的R分成8组,每组4bits,\\每组最前和最后各加1bits,不是随便加,按图中所给的表进行扩展
我觉得这里对照下面的图看是能看懂的,先将32bits的R分成8组,每组4bits,每组最前和最后各加1bits,不是随便加,按图中所给的表进行扩展

不好理解的话举个例子:①中是
32
b
i
t
s
的数据,按照置换表进行置换后得到③④
(此过程和最开始的
I
P
置换的原理和过程是一样的)
扩展后得到
48
b
i
t
s
不好理解的话举个例子:①中是32bits的数据,按照置换表进行置换后得到③④\\(此过程和最开始的IP置换的原理和过程是一样的)\\扩展后得到48bits
不好理解的话举个例子:①中是32bits的数据,按照置换表进行置换后得到③④(此过程和最开始的IP置换的原理和过程是一样的)扩展后得到48bits

轮函数–与子密钥异或( 48 − > 48 48->48 48−>48)
上一步得到的拓展流与子密钥异或 , 子密钥均为 48 b i t s ( 为什么是 48 b i t s ,文章最后来讲 ) 上一步得到的拓展流与子密钥异或,子密钥均为48bits\\(为什么是48bits,文章最后来讲) 上一步得到的拓展流与子密钥异或,子密钥均为48bits(为什么是48bits,文章最后来讲)
轮函数–S盒压缩处理( 48 − > 32 48->32 48−>32)
首先先将
48
b
i
t
s
输入等分为
8
块,每块
6
b
i
t
s
,
压缩后得到
4
位的输出,最终得到
32
b
i
t
s
输出,那如何进行压缩呢?(请移步下图的举例)
首先先将48bits输入等分为8块,每块6bits,\\压缩后得到4位的输出,最终得到32bits输出,那如何进行压缩呢?(请移步下图的举例)
首先先将48bits输入等分为8块,每块6bits,压缩后得到4位的输出,最终得到32bits输出,那如何进行压缩呢?(请移步下图的举例)


举个例子:
例如前
6
位
111111
,取头尾两个结合得到二进制
11
,转为
10
进制
3
,将其作为行数
中间四位数据组合得到二进制
1111
,转为
10
进制
15
,将其作为列数,
到
S
盒中相应的行列中去找,得到
13
,
13
转成的二进制数
1101
即为最终结果
自此,
6
b
i
t
s
−
>
4
b
i
t
s
,
48
b
i
t
s
−
>
32
b
i
t
s
举个例子:\\例如前6位111111,取头尾两个结合得到二进制11,转为10进制3,将其作为行数\\中间四位数据组合得到二进制1111,转为10进制15,将其作为列数,\\到S盒中相应的行列中去找,得到13,13转成的二进制数1101即为最终结果\\自此,6bits->4bits,48bits->32bits
举个例子:例如前6位111111,取头尾两个结合得到二进制11,转为10进制3,将其作为行数中间四位数据组合得到二进制1111,转为10进制15,将其作为列数,到S盒中相应的行列中去找,得到13,13转成的二进制数1101即为最终结果自此,6bits−>4bits,48bits−>32bits
注意:行列都是从0开始,故等下代码阶段在S盒中找数,行列不需减一


轮函数–P盒置换
S
盒所得结果再经过
P
盒置换(与初始
I
P
置换过程相同)。
至此,一次轮函数操作完毕
S盒所得结果再经过P盒置换(与初始IP置换过程相同)。\\至此,一次轮函数操作完毕
S盒所得结果再经过P盒置换(与初始IP置换过程相同)。至此,一次轮函数操作完毕

异或
一次轮函数加密后的数据与 L i − 1 进行异或即可得到 R i ( R i = L i − 1 ⊕ f ( R i − 1 , K i ) ) 自此,一轮迭代完成 一次轮函数加密后的数据与L_{i-1}进行异或即可得到R_{i}(R_i = L_{i-1} \oplus f(R_{i-1}, K_i))\\自此,一轮迭代完成 一次轮函数加密后的数据与Li−1进行异或即可得到Ri(Ri=Li−1⊕f(Ri−1,Ki))自此,一轮迭代完成
IP逆置换
进行 16 轮相同的运算,得到 L 16 , R 16 后将其进行拼接得到 64 b i t s 的数据, 将该 64 b i t s 的数据进行 I P 逆置换后即可得到最终密文 进行16轮相同的运算,得到L_{16},R_{16}后将其进行拼接得到64bits的数据,\\将该64bits的数据进行IP逆置换后即可得到最终密文 进行16轮相同的运算,得到L16,R16后将其进行拼接得到64bits的数据,将该64bits的数据进行IP逆置换后即可得到最终密文
注意:以上所有置换表都是已知的,固定的,给定的,不可改的(但如果有人拿此出题进行修改就不好说了)
接下来讲讲密钥生成
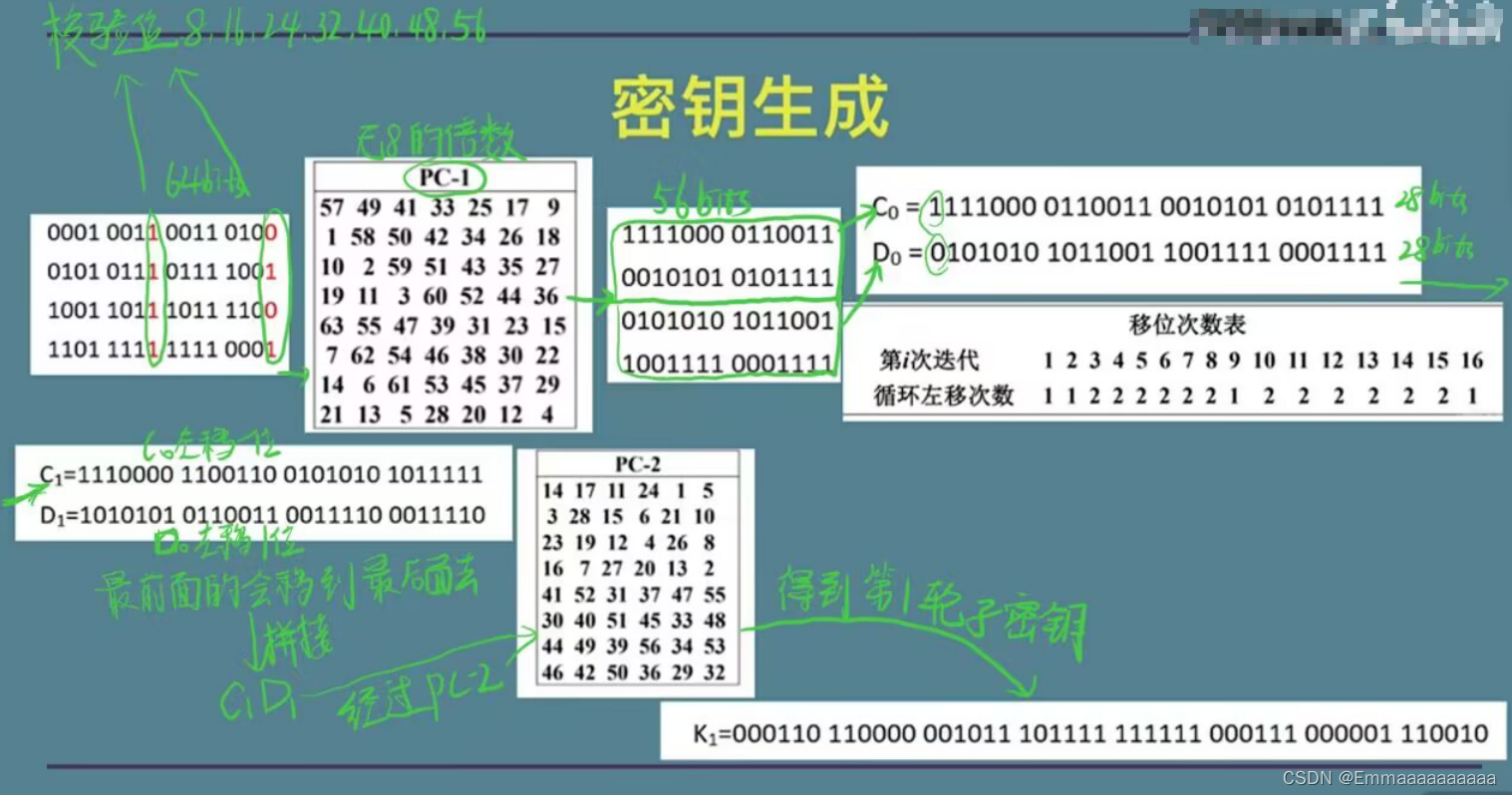
密钥生成
64
b
i
t
s
密钥(种子密钥),首先通过
P
C
−
1
表的置换得到
56
b
i
t
s
数据
(里面无
8
的倍数,故该表的主要作用是去除校验码)
平分分别得到
28
b
i
t
s
的
C
0
,
D
0
根据移位次数表将
C
,
D
进行左移
第一次:将
C
0
,
D
0
左移
1
位得到
C
1
,
D
1
将
C
1
,
D
1
进行拼接再通过
P
C
−
2
表置换得到第一轮子密钥
K
1
第二次:将
C
1
,
D
1
左移
1
位得到
C
2
,
D
2
将
C
2
,
D
2
进行拼接再通过
P
C
−
2
表置换得到第一轮子密钥
K
2
第三次:将
C
2
,
D
2
左移
2
位得到
C
3
,
D
3
将
C
3
,
D
3
进行拼接再通过
P
C
−
2
表置换得到第一轮子密钥
K
3
以此类推,最终生成
16
轮子密钥
64bits密钥(种子密钥),首先通过PC-1表的置换得到56bits数据\\(里面无8的倍数,故该表的主要作用是去除校验码)\\平分分别得到28bits的C_{0},D_{0}\\根据移位次数表将C,D进行左移\\ 第一次:将C_{0},D_{0}左移1位得到C_{1},D_{1}\\ \hspace{4em}将C_{1},D_{1}进行拼接再通过PC-2表置换得到第一轮子密钥K_{1}\\ 第二次:将C_{1},D_{1}左移1位得到C_{2},D_{2}\\ \hspace{4em}将C_{2},D_{2}进行拼接再通过PC-2表置换得到第一轮子密钥K_{2} \\ 第三次:将C_{2},D_{2}左移2位得到C_{3},D_{3}\\ \hspace{4em}将C_{3},D_{3}进行拼接再通过PC-2表置换得到第一轮子密钥K_{3}\\ 以此类推,最终生成16轮子密钥
64bits密钥(种子密钥),首先通过PC−1表的置换得到56bits数据(里面无8的倍数,故该表的主要作用是去除校验码)平分分别得到28bits的C0,D0根据移位次数表将C,D进行左移第一次:将C0,D0左移1位得到C1,D1将C1,D1进行拼接再通过PC−2表置换得到第一轮子密钥K1第二次:将C1,D1左移1位得到C2,D2将C2,D2进行拼接再通过PC−2表置换得到第一轮子密钥K2第三次:将C2,D2左移2位得到C3,D3将C3,D3进行拼接再通过PC−2表置换得到第一轮子密钥K3以此类推,最终生成16轮子密钥

代码部分
# 本脚本名: __table.py
# 明文M 的初始置换 IP
IP = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7] # 将明文中的第58位换到第一位
# 逆初始置换 IP^-1
IP_INV = [40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25]
# 右子密钥扩展表 32->48位
E = [32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1]
# 轮结构中的F函数中的置换P
P = [16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25]
# 压缩置换: 64位母密钥->56位母密钥
PC_1 = [57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4]
# 压缩置换: 56位左右密钥->48位子密钥
PC_2 = [14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32]
# 左右子密钥的循环移位表
ROTATE = [1, 1, 2, 2, 2, 2, 2, 2,
1, 2, 2, 2, 2, 2, 2, 1]
# 8 个 S 盒
SBOX = [
[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],
[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],
[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],
[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],
[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],
[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],
[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],
[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]]
# 本脚本名: __util.py
from __table import *
import time
def permutate(bitstr, table):
""" 通用置换运算
@table: 置换盒
"""
res = ""
for i in table:
res += bitstr[i-1] # 下标从0开始,故减一
return res
def leftShift(key, num):
""" 子密钥LR: 左循环移位
@key: 待移位的子密钥
@num: 列表左移位位数
"""
return key[num:] + key[0:num]
def XOR(str1, str2):
""" 两比特串进行异或 """
res = ""
for i in range(0, len(str1)):
xor = int(str1[i]) ^ int(str2[i])
res += str(xor)
return res
def Sbox(binstr):
""" S盒置换: 48位->32位 """
box = 0 # S盒的索引
res = ""
for i in range(0, len(binstr), 6):
tmp = binstr[i:i+6]
row = int(tmp[0] + tmp[5], 2) # 头尾数据结合成的2进制数据转化为10进制作为行数
col = int(tmp[1:5], 2) # 中间4位数据结合成的2进制数据转换为10进制作为列数
num = bin(SBOX[box][16*row+col])[2:].zfill(4) # 0是包含在里面的,所以不需要row-1,都是从0开始的。然后将在s盒中查到的数值转化为4位的2进制数
# zfill(4) 不足4位左侧填充0以补全4位
# 这样将48位分成8 * 6 ,然后6->4,最后得到8 * 4 = 32比特的数据
res += num
box += 1
return res
def createSubKey(key64):
""" 64位母密钥->16轮的48位子密钥列表
@key64: 输入的64位加密密钥
@return: 16轮子密钥列表
"""
subkey = []
key56 = permutate(key64, PC_1) # 64位密钥压缩置换,64bits变58bits(将校验位去除)
C28b, D28b = key56[0:28], key56[28:] # 56位密钥左右平分
for i in range(16):
C28b = leftShift(C28b, ROTATE[i]) # 左循环移位
D28b = leftShift(D28b, ROTATE[i]) # 左循环移位
subkey.append(permutate(C28b + D28b, PC_2)) # 得到一轮子密钥,加到子密钥subkey列表中去
return subkey
def turnFunction(R32b, subkey):
""" 轮结构中的F函数
@R32b: F函数输入参数 32位的右明文
@subkey: F函数输入参数 48位子密钥
"""
R48b = permutate(R32b, E) # E盒扩展: 右明文32位->48位
# E扩展置换,将32位输入扩展为48位输出(要与48比特的密钥进行运算(密钥中58位参与运算,但如何到48比特,密钥生成过程中会讲,如今已知的是K1到K16都是48比特的子密钥))
R48b = XOR(R48b, subkey) # 两异或: 扩展流与子密钥异或 R_(i-1) ^ K_i
R32b = Sbox(R48b) # S盒压缩: 压缩48位->32位
Fout = permutate(R32b, P) # P盒置换
return Fout # 至此,一次轮函数操作完毕
def hexToBit(hexstr):
""" 十六进制字符串->二进制比特流(每字符4位) """
binstr = ""
for i in hexstr:
binstr += bin(int(i,16))[2:].zfill(4)
return binstr
def bitToHex(bitstr):
""" 二进制比特流->十六进制字符串 """
hexstr = ""
for i in range(0, len(bitstr), 4):
hexstr += hex(int(bitstr[i:i+4], 2))[2:].upper()
return hexstr
def takeTime(func):
""" 装饰器: 计算函数运行耗时"""
def decorated(*args):
startime = time.time()
func(*args)
endtime = time.time()
taketime = round((endtime - startime)*10**6)
print(f"\n->运算耗时: {taketime} 微秒")
return func(*args)
return decorated
# 本脚本名: des.py
from __util import *
class DES():
""" DES 加解密 """
def __init__(self, scrkey):
self.scrkey = hexToBit(scrkey) # 初始化密钥 16进制字符->比特流 ,也叫种子密钥
def feistel(self, in64bit, flag):
""" Feistel 网络结构算法
@in64bit: 输入64位比特流
@flag: 正向算法/反向算法,正向为1,反向为0
单字符由8比特表示
"""
bit64 = permutate(in64bit, IP) # 初置换IP重排明文
L32b, R32b = bit64[0:32], bit64[32:] # 64位明文左右平分
subkey = createSubKey(self.scrkey) # 生成所有的子密钥
if flag == 0: subkey = subkey[::-1] # 解密用的逆子密钥
for i in range(16):
Fout = turnFunction(R32b, subkey[i])
L32b, R32b = R32b, XOR(L32b, Fout)
out64bit = permutate(R32b + L32b, IP_INV) # 左右交换 逆初始置换
return out64bit
@takeTime
def encrypt(self, messag):
""" DES加密
@messag: 16进制明文字符串
@return: 16进制密文字符串
"""
mesbit = hexToBit(messag)
cipbit = self.feistel(mesbit, 1)
cipher = bitToHex(cipbit)
return cipher
@takeTime
def decrypt(self, cipher):
""" DES 解密
@cipher: 16进制密文字符串
"""
cipher = hexToBit(cipher)
mesbit = self.feistel(cipher, 0)
messag = bitToHex(mesbit)
return messag
if __name__ == '__main__':
scrkey = "133457799BBCDFF1"
messag = "0123456789ABCDEF"
cipher = "85E813540F0AB405"
crypto = DES(scrkey)
print("16进制密文:", crypto.encrypt(messag))
print("16进制明文:", crypto.decrypt(cipher))
参考
https://www.bilibili.com/video/BV1KQ4y127AT/?spm_id_from=333.880.my_history.page.click&vd_source=0bd1680dd495123dd54d157e522a2e86
https://blog.csdn.net/Alpherkin/article/details/121198150?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522168929564016800211547104%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=168929564016800211547104&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allfirst_rank_ecpm_v1~rank_v31_ecpm-7-121198150-null-null.142v88control_2,239v2insert_chatgpt&utm_term=feistel%E5%8A%A0%E8%A7%A3%E5%AF%86%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4187
持续更新中…
(后续会上题)


![[oeasy]python0072_整数类型_int_integer_整型变量](https://img-blog.csdnimg.cn/img_convert/652b3be561f0441892198122b83757cb.png)


![[论文分享]TS-TCC:基于时间和语境对比的时间序列表征学习](https://img-blog.csdnimg.cn/img_convert/46eb86614e3e781ceec8569e4f9bc198.png)