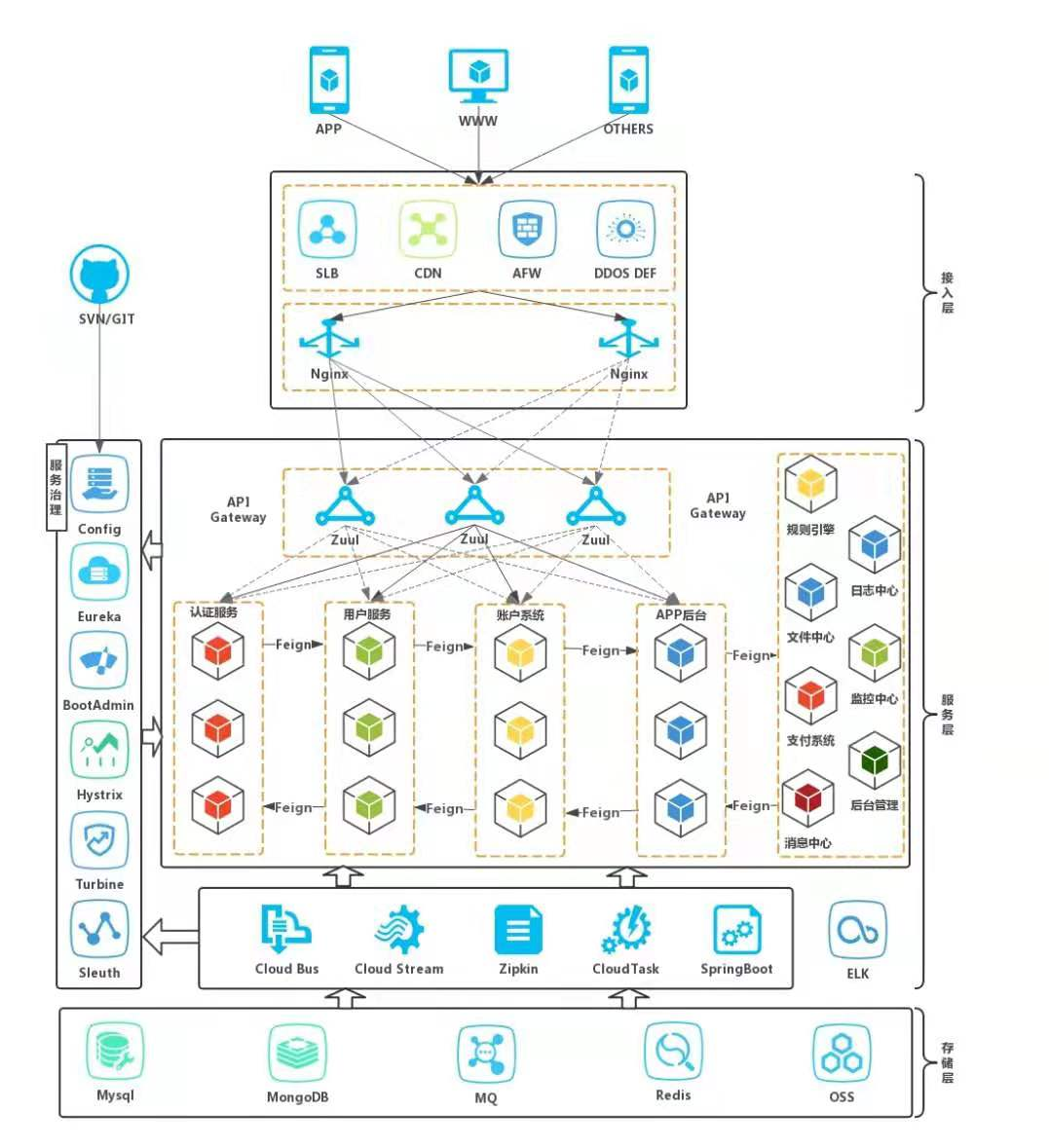
《算法竞赛·快冲300题》每日一题：“推箱子”

news2024/11/26 14:48:02

《算法竞赛·快冲300题》将于2024年出版，是《算法竞赛》的辅助练习册。
所有题目放在自建的OJ New Online Judge。
用C/C++、Java、Python三种语言给出代码，以中低档题为主，适合入门、进阶。

文章目录

题目描述
题解
C++代码
Java代码
Python代码

“ 推箱子” ，链接： http://oj.ecustacm.cn/problem.php?id=1819

题目描述

【题目描述】 在一个高度为H的箱子前方，有一个长和高为N的障碍物。
障碍物的每一列存在一个连续的缺口，第i列的缺口从第l个单位到第h个单位（从底部由0开始数）。
现在请你清理出一条高度为H的通道，使得箱子可以直接推出去。
请输出最少需要清理的障碍物面积。
如下图为样例中的障碍物，长和高度均为5，箱子高度为2。不需要考虑箱子会掉入某些坑中。最少需要移除两个单位的障碍物可以造出一条高度为2的通道。
在这里插入图片描述

【输入格式】 输入第一行为两个正整数N和H，表示障碍物的尺寸和箱子的高度，1≤H≤N≤1000000。
接下来N行，每行包含两个整数li和hi，表示第i列缺口的范围，0≤li≤hi<N。
【输出格式】 输出一个数字表示答案。
【输入样例】

【输出样例】

题解

箱子高度为H，检查障碍物中的连续H行，看哪H行需要清理的障碍物最少，或者哪H行中的空白最多。在输入样例中，障碍物共5行，这5行中的空白数量从底部开始往上数分别是(0, 2, 5, 3, 0)，其中(5, 3)这2行的空白最多，是5+3=8，需要移除的障碍物数量是N×H-8=5×2-8=2。
用数组a[]表示障碍物，a[i]是障碍物第i行的空白数量。把题目抽象为：a[]是N个整数，从a[]中找出连续的H个整数，要求它们的和最大。
先考虑用暴力法求解。
（1）如果用暴力法从左到右依次对a[]中的H个整数求和，找到最大的和，总计算量是O(NH)的，超时。
（2）也需要注意输入的问题。题目按列给出空白数量，需要转换为行的空白数量。如果简单地转换，计算量太大。例如样例第1列的空白位置是(2, 3)，需要赋值a[2]++、a[3]++。一列有H个空白，a[]数组需要赋值H次，N列的总计算量是O(NH)，超时。
本题用差分和前缀和来优化。
（1）用差分处理输入。下面代码第9行读一个列的起点位置li和终点位置hi，代码第10行和第11行输入到d[]，d[]是a[]的差分。计算量仅为O(N)。
（2）用前缀和求区间和。第14行用d[]求a[]；第16行计算a[]的前缀和sum[]；第18、19行找到最大的区间和。计算量仅为O(N)。。
【笔记】 通过本题熟悉差分和前缀和的应用。

C++代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
ll d[N], a[N], sum[N];
int main(){
    int n, h;   scanf("%d%d",&n,&h);
    for(int i = 1; i <= n; i++) {
        int li, hi;     scanf("%d%d",&li,&hi);       //本题n≤1000000，用scanf输入比cin快
        d[li]++;                                             //可替换为  sum[li]++;
        d[hi+1]--;                                           //可替换为  sum[hi+1]--;
    }
    //用差分数组计算原数组
    for(int i = 1; i <= n; i++)  a[i] = a[i-1] + d[i-1];     //可替换为  sum[i] += sum[i-1];
    //用原数组计算前缀和数组
    for(int i = 1; i <= n; i++)  sum[i] = sum[i-1] + a[i];   //可替换为  sum[i] += sum[i-1];
    ll ans = sum[h-1];
    for(int left = 1; left+h-1 <= n; left++)
        ans = max(ans, sum[left+h-1] - sum[left-1]);
    cout << (ll)n * h - ans << endl;
    return 0;
}

Java代码

import java.util.*;
import java.io.*;
public class Main{
    static int N = 1_000_010;
    static long[] d = new long[N], a = new long[N], sum = new long[N];
    public static void main(String[] args) throws Exception{
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt(), h = scan.nextInt();
        for(int i = 1; i <= n; i++) {
            int li = scan.nextInt(), hi = scan.nextInt();
            d[li]++;
            d[hi+1]--;
        }
        for(int i = 1; i <= n; i++)  a[i] = a[i-1] + d[i-1];   //用差分数组计算原数组
        for(int i = 1; i <= n; i++)  sum[i] = sum[i-1] + a[i]; //用原数组计算前缀和数组
        long ans = sum[h-1];
        for(int left = 1; left+h-1 <= n; left++)
            ans = Math.max(ans, sum[left+h-1] - sum[left-1]);
        System.out.println((long)n * h - ans);
    }
}

Python代码

import sys
input=sys.stdin.readline                       #加这句后读入会快些
n, h = map(int, input().split())
d, a, sum = [0] * (n+10), [0] * (n+10), [0] * (n+10)
for i in range(1, n+1):
    li, hi = map(int, input().split())
    d[li] += 1
    d[hi+1] -= 1
for i in range(1, n+1):  a[i] = a[i-1] + d[i-1]     #用差分数组计算原数组
for i in range(1, n+1):  sum[i] = sum[i-1] + a[i]   #用原数组计算前缀和数组
ans = sum[h-1]
for left in range(1, n-h+2):  ans = max(ans, sum[left+h-1] - sum[left-1])
print(n * h - ans)