文章目录
- 一、排序的概念
- 排序的概念
- 排序的稳定性
- 七大排序算法
- 二、快速排序
- 核心思想
- Hoare法
- 挖坑法
- 前后指针法(选学)
- 三、性能分析
- 四、算法优化
- 优化基准的选取
- 优化少量数据时的排序方案
- 优化后的完整代码
- 五、七大排序算法
一、排序的概念
排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
排序的稳定性
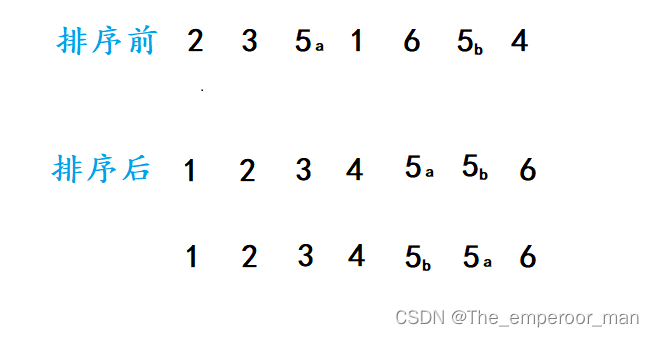
上述待排序的数中,有两个5。 将前面的5标记一个a, 将后面的5标记一个b。
通过算法进行排序后,这一组数就有序了, 但是要看两个相同的5的位置是否有改变。
5a仍在5b前面,那么这个排序算法就是稳定的 ,
5a跑到了5b后面,那么这个排序算法就是不稳定的 。
一个稳定的排序算法可以做到不稳定,
不稳定的排序算法一定做不到稳定。
至于为什么要讨论这个稳定性, 是为了以后应用到实际场景上。 比如,一场数学考试, 假设a用了30分钟做完了,并得了满分。
假设b用了一个小时做完了,并得了满分。 此时a与b都是得了满分,但是用的时间不一样,所以两个人的排名又会有所不同。
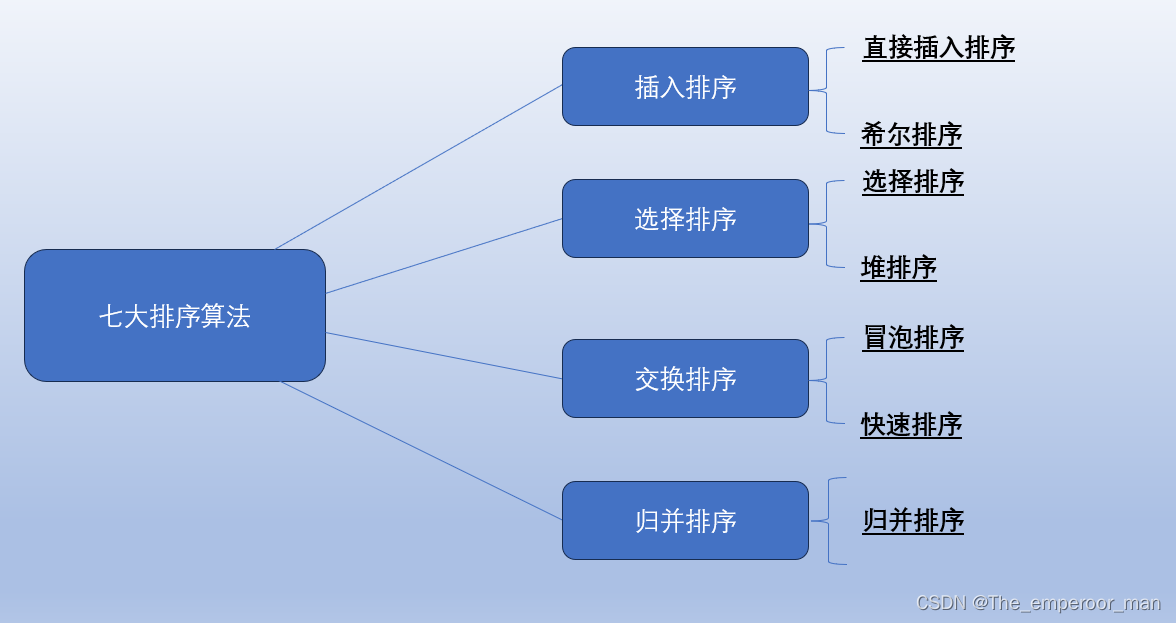
七大排序算法
二、快速排序
核心思想
基本思想:任取待排序元素序列中的某元素作为基准值,将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
public static void quickSort(int[] array) {
quick(array,0, array.length-1);
}
private static void quick(int[] array,int left,int right) {
// 此处的一定要是大于等于
// 如果往下递归出现了piovt == 0的情况,
// 那么再递归进去,left == 0,right == -1,
// 此时就要结束递归
if(left >= right) {
return;
}
// partition方法功能:将选取的基准值放到合适的位置,并返回基准值下标
int piovt = partition(array,left,right);
// 通过递归的方式,对左右子序列分别找寻基准值并放到合适位置,从而达到排序目的
quick(array, left, piovt-1);
quick(array,piovt+1,right);
}
共有三种方法可以实现该思想。
Hoare法
图解
有一组待排序数列,我们进行升序排序。
代码
public static void quickSort(int[] array) {
quick(array,0, array.length-1);
}
private static void quick(int[] array,int left,int right) {
if(left >= right) {
return;
}
int piovt = partition1(array,left,right);
quick(array, left, piovt-1);
quick(array,piovt+1,right);
}
//Hoare法
private static int partition(int[] array,int left,int right) {
// 基准值
int tmp = array[left];
// 基准下标
int index = left;
while (left < right) {
// 让right找比tmp小的数
while (right > left && array[right] >= tmp) {
right--;
}
// 让left找比tmp大的数
while (left < right && array[left] <= tmp) {
left++;
}
// 让left与right这两个数进行交换
swap(array,left,right);
}
// 将基准值放到合适的位置
swap(array,index,right);
// 返回基准下标
return right;
}
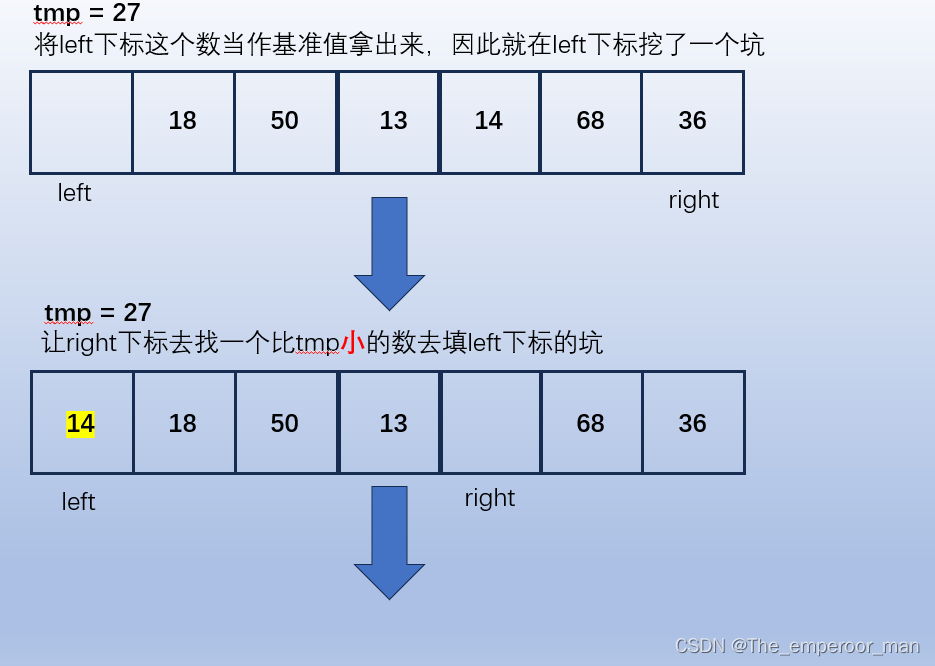
挖坑法
挖坑发是后人对Hoare法的另一种实现方式。
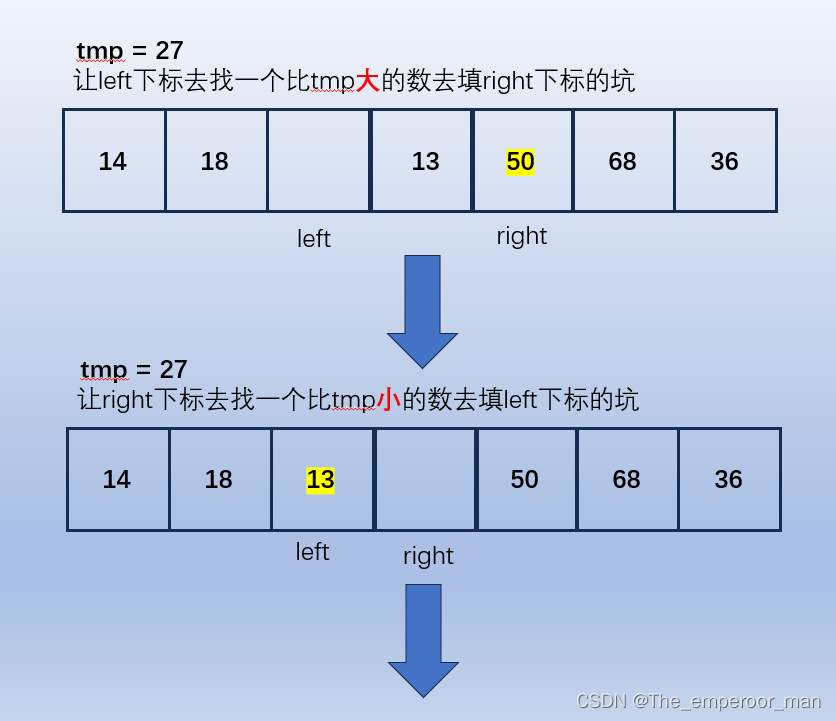
图解
有一组待排序数列,我们进行升序排序。
注意left与right的区别,别看错了就搞不懂了。
代码
public static void quickSort(int[] array) {
quick(array,0, array.length-1);
}
private static void quick(int[] array,int left,int right) {
if(left >= right) {
return;
}
int piovt = partition(array,left,right);
quick(array, left, piovt-1);
quick(array,piovt+1,right);
}
//挖坑法
private static int partition(int[] array,int left,int right) {
// 在left下标挖一个坑
int tmp = array[left];
while (left < right) {
// 让right下标去找比tmp小的数
while (right > left && array[right] >= tmp) {
right--;
}
// 填left下标的坑,此时right下标变成一个坑了
array[left] = array[right];
// 让left下标去找比tmp大的数
while (left < right && array[left] <= tmp) {
left++;
}
// 填right下标的坑,此时left下标变成一个坑了
array[right] = array[left];
}
// 将基准值放到合适的位置
array[left] = tmp;
// 返回基准下标
return left;
}
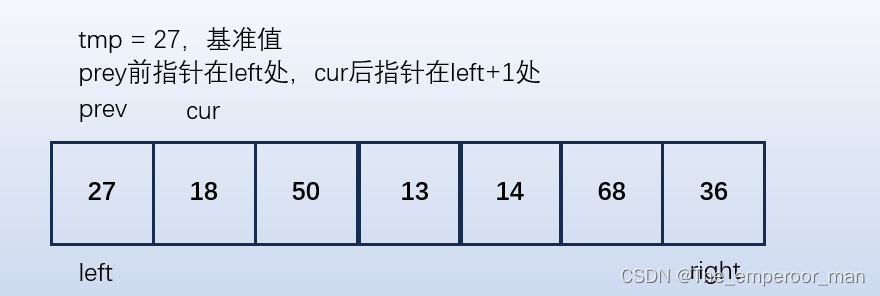
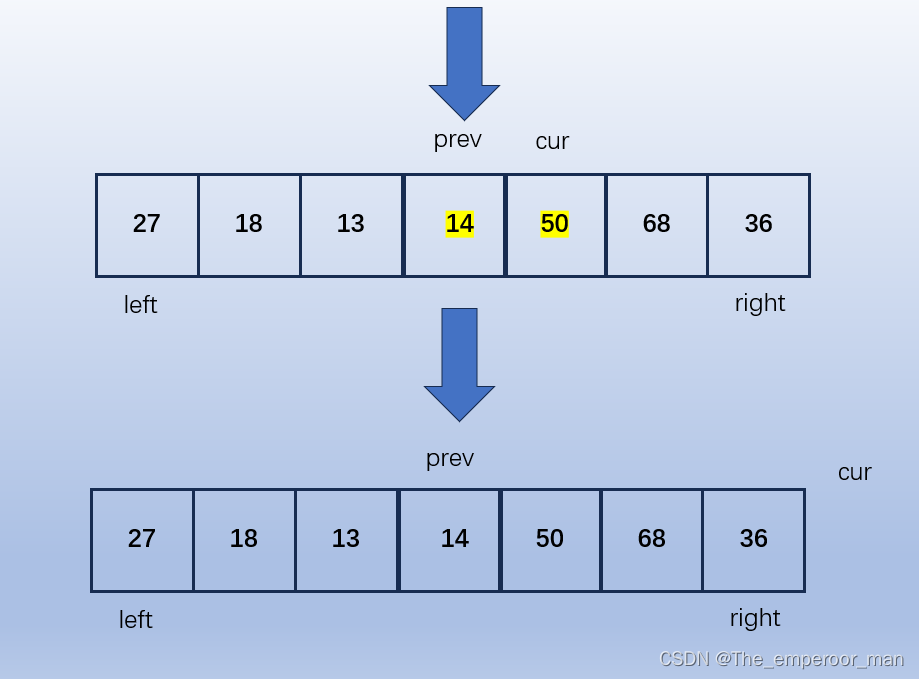
前后指针法(选学)
图解
有一组待排序数列,我们进行升序排序。
代码
public static void quickSort(int[] array) {
quick(array,0, array.length-1);
}
private static void quick(int[] array,int left,int right) {
if(left >= right) {
return;
}
int piovt = partition(array,left,right);
quick(array, left, piovt-1);
quick(array,piovt+1,right);
}
// 前后指针法
private static int partition(int[] array, int left, int right) {
int prev = left ;
int cur = left+1;
while (cur <= right) {
// 此处当第一个判断语句不满足时,
// 不会触发第二个判断语句,
// 会跳出if语句
// 因此不是每次if进行判断时,都会执行++prev
if(array[cur] < array[left] && array[++prev] != array[cur]) {
swap(array,cur,prev);
}
cur++;
}
swap(array,prev,left);
return prev;
}
private static void swap(int[] array,int a,int b) {
int tmp = array[a];
array[a] = array[b];
array[b] = tmp;
}
三、性能分析
最好情况
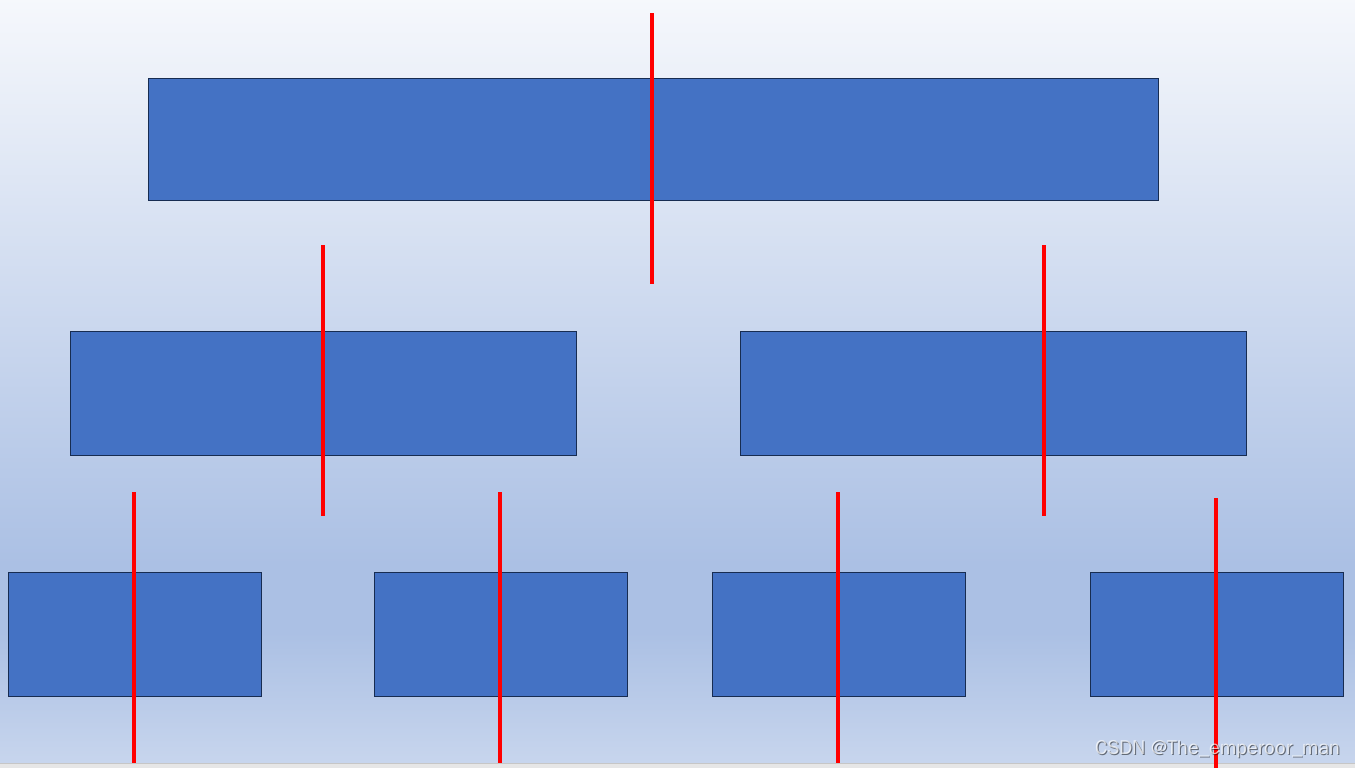
每次找到的基准都能平均将数据分为两组
那么此时一共有log(n)层,每层都有n个数据,这n个数据都要遍历一遍,因此
时间复杂度:O(n*log(n)),
此时会先遍历左树,因此空间复杂度为树的高度即层数
空间复杂度:log(n).
不相邻间元素发送了交换
稳定性:不稳定
最坏情况
需要排序的数列本身就是一个顺序或逆序的数列,此时找到的基准就会每次都分成极端的两组,一组一个数没有,另一组有n-1个数(这两组的边界一个是基准-1,一个是基准+1)
此时就会有n层,每层也有n个数据
此时
时间复杂度:O(n2)
空间复杂度为树的高度即层数
空间复杂度:n
不相邻间元素发送了交换
稳定性:不稳定
四、算法优化
快速排序在最坏情况下,时间复杂度竟然达到了O(n2),这哪里快速啊,所以下面就要进行优化了。
优化基准的选取
共有两种方案: 1️⃣随机选取基准法,这要是倒霉起来,依然有可能会次次都随机选到最极端最坏的情况,所以这个不用。 2️⃣三数取中法,这个可以保证不会让你选到最极端最坏的情况。
三数取中法:在上面的算法中,我们的基准选取的都是left下标,
而三数取中指的是在left,right,mid( (left + right)/2 )这三个下标在中选取一个中间值作为基准,不是最大也不是最小,就保证了不会出现极端情况。
出现了以上的最坏情况,也就是让快速排序变成了二分查找。
private static int minThree(int[]array,int left,int right) {
//三数取中法,优化递归实现的快速排序
//使得最坏情况时,快速排序变为二分查找
int mid = (left+right)/2;
if(array[right] > array[left]) {
int tmp = left;
left = right;
right = tmp;
}
if(array[mid] > array[left]) {
return left;
}
if(array[mid] > array[right]) {
return mid;
}
return right;
}
优化少量数据时的排序方案
数据量大时
就像二叉树一样,每一组数据往下走一层都会被分成两组,而到了最后几层,则会因为数据量的庞大而被分成许多组进行递归,此时的递归开销就会很大,很有可能导致~~栈溢出~~,
因此我们可以设定一个数量闸口,当每组的数据小的到了这个闸口,就采用比较简单的直接插入排序。
而且在快速排序的不断递归下,数据一定是越来越有序的,直接插入排序的效率也会更高。
数据小时
此时即便是一开始就用直接插入排序,时间也会相差无几。
优化后的完整代码
public class QuickSort {
/**
* 快速排序
* 时间复杂度:代码未优化时:最好情况(满二叉树或完全二叉树):O(n*logn), 最坏情况(顺序和逆序时):O(n^2)
* 空间复杂度:代码未优化时:最好情况(满二叉树或完全二叉树):O(logn), 最坏情况(顺序和逆序时):O(n)
* 稳定性:不稳定
* @param array
*/
public static void quickSort(int[] array) {
quick(array,0, array.length-1);
}
private static void quick(int[] array,int left,int right) {
if(left >= right) {
return;
}
// 设置数量闸口,
// 数量小,使用直接插入排序
if(right - left + 1 < 14) {
InsertSort(array);
return;
}
// 将三数取中法取得的中间值换到left处
swap(array,minThree(array,left,right),left);
int piovt = partition(array,left,right);
quick(array, left, piovt-1);
quick(array,piovt+1,right);
}
//挖坑法
private static int partition(int[] array,int left,int right) {
// 在left下标挖一个坑
int tmp = array[left];
while (left < right) {
// 让right下标去找比tmp小的数
while (right > left && array[right] >= tmp) {
right--;
}
// 填left下标的坑,此时right下标变成一个坑了
array[left] = array[right];
// 让left下标去找比tmp大的数
while (left < right && array[left] <= tmp) {
left++;
}
// 填right下标的坑,此时left下标变成一个坑了
array[right] = array[left];
}
// 将基准值放到合适的位置
array[left] = tmp;
// 返回基准下标
return left;
}
//Hoare法
private static int partition3(int[] array,int left,int right) {
// 基准值
int tmp = array[left];
// 基准下标
int index = left;
while (left < right) {
// 让right找比tmp小的数
while (right > left && array[right] >= tmp) {
right--;
}
// 让left找比tmp大的数
while (left < right && array[left] <= tmp) {
left++;
}
// 让left与right这两个数进行交换
swap(array,left,right);
}
// 将基准值放到合适的位置
swap(array,index,right);
// 返回基准下标
return right;
}
//前后指针法
private static int partition2(int[] array, int left, int right) {
int prev = left ;
int cur = left+1;
while (cur <= right) {
if(array[cur] < array[left] && array[++prev] != array[cur]) {
swap(array,cur,prev);
}
cur++;
}
swap(array,prev,left);
return prev;
}
private static int minThree(int[]array,int left,int right) {
//三数取中法,优化递归实现的快速排序
//使得最坏情况时,快速排序变为二分查找
int mid = (left+right)/2;
if(array[right] > array[left]) {
int tmp = left;
left = right;
right = tmp;
}
if(array[mid] > array[left]) {
return left;
}
if(array[mid] > array[right]) {
return mid;
}
return right;
}
private static void swap(int[] array,int a,int b) {
int tmp = array[a];
array[a] = array[b];
array[b] = tmp;
}
}
五、七大排序算法

想学哪个点哪个
归并排序讲解
快速排序讲解
直接插入排序讲解
希尔排序讲解
直接选择排序讲解
堆排序讲解
冒泡排序讲解