💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码及文章讲解
💥1 概述
文献来源:

结果表明,即使缺少某些测量的强度样本,也可以从其衍射图或全息图中成功检索物体分布。允许的最大缺失值数取决于线性过采样比率 s,其中 s 的值越高,丢失的样本强度就越多。对于实值物体,缺失像素与像素总数的比率不应分别超过采集的衍射图案或全息图中的(1 - 2/s^2)或(1 - 1/s^2)。例如,在 s = 5 的过采样比率下,即使是测量强度值的 8% 也足以同时检索对象分布和缺失强度值。重要的是,缺失的强度值不应集中在中心,而应随机分布在获得的衍射图案上。
原文摘要:
It is demonstrated that an object distribution can be successfully retrieved from its diffraction pattern or hologram, even if some of the measured intensity samples are missing. The maximum allowable number of missing values depends on the linear oversampling ratio s, where the higher the value of s, the more intensity samples can be missing. For a real-valued object, the ratio of missing pixels to the total number of pixels should not exceed (1 - 2/s^2) or (1 - 1/s^2) in the acquired diffraction pattern or hologram, respectively. For example, even 5% of the measured intensity values at an oversampling ratio of s = 8 are sufficient to simultaneously retrieve the object distribution and the missing intensity values. It is important that the missing intensity values should not be concentrated in the centre, but should be randomly distributed over the acquired diffraction pattern.
Coherent diffraction imaging Holography Iterative phase retrieval Nyquist–Shannon theorem Sampling rate
📚2 运行结果
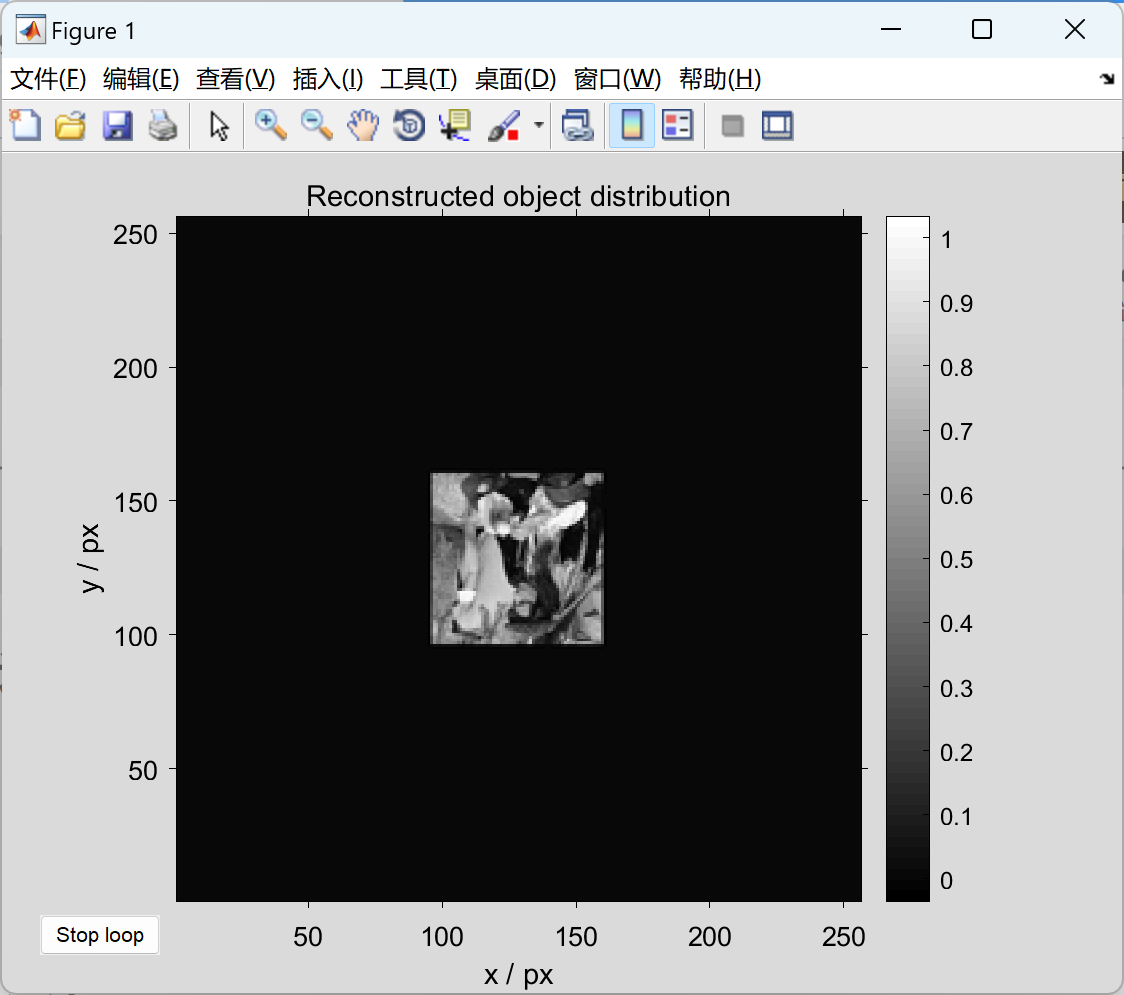

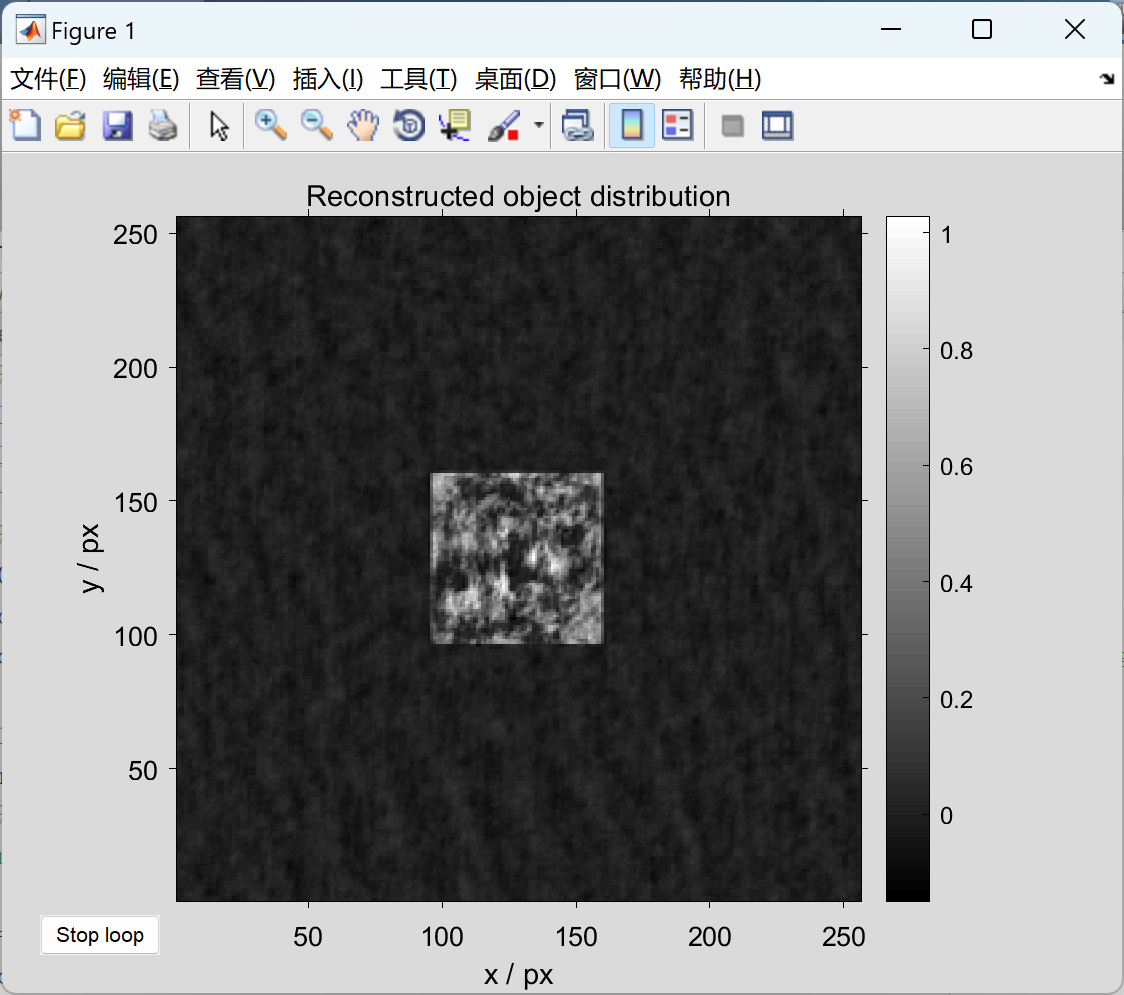
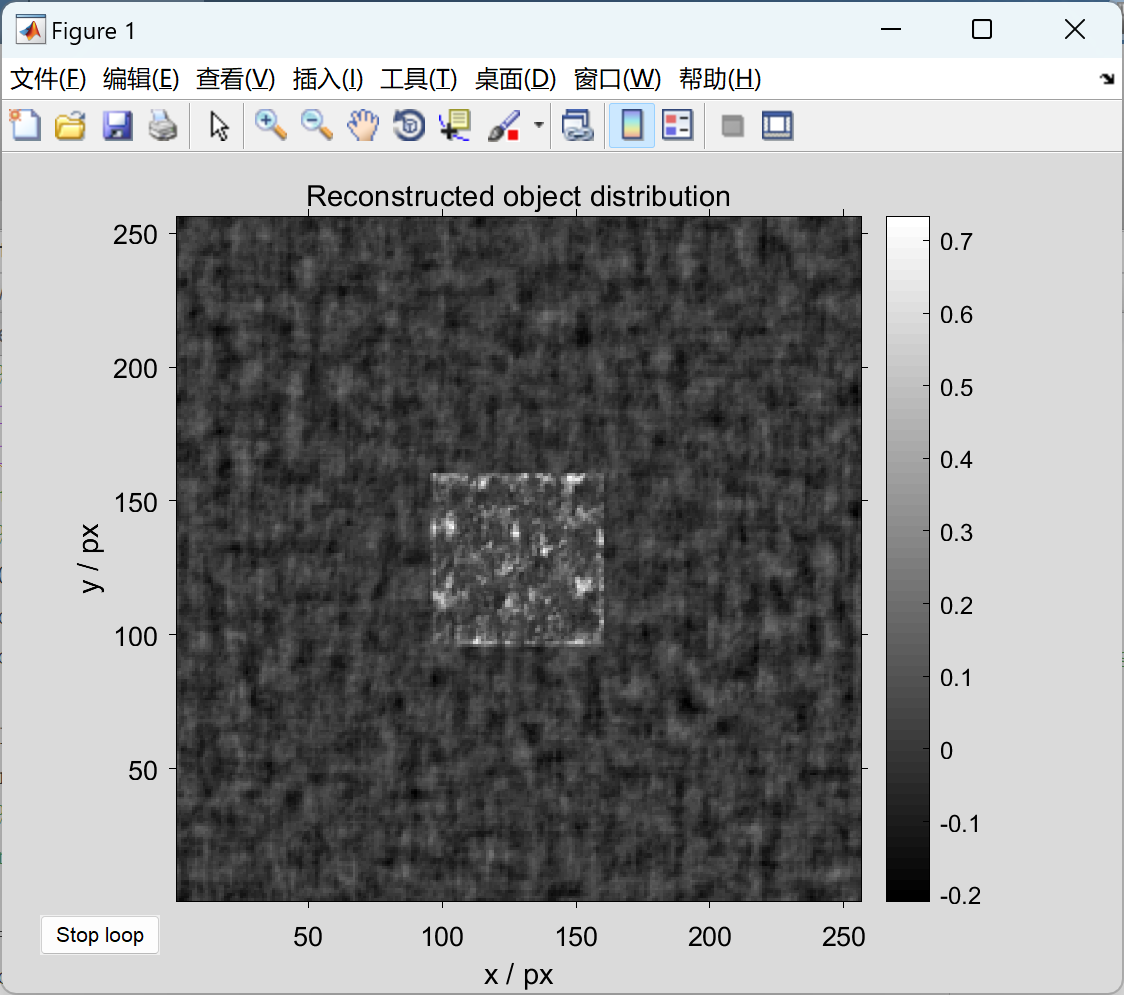
部分代码:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
beta = 0.9; % parameter in HIO algorithm
treshold = 1; % treshold in the object domain
Iterations = 2000; % number of iterative loops, typically 200 iterations are enough
N = 512; % number of pixels
p = 0.01; % time to pause, otherwise images are not shown
Reconstructions = 100; % number of reconstructions
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Reading diffraction pattern
fid = fopen('a_dp.bin', 'r');
dp = fread(fid, [N, N], 'real*4');
fclose(fid);
dp_amplitude(:,:) = sqrt(dp(:,:));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Finding pixels with values zero
mask = ones(N,N);
for ii=1:N
for jj=1:N
if ((dp_amplitude(ii,jj) == 0))
mask(ii,jj) = 0;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Creating support in object domain
support = zeros(N,N);
R = N/8;
for m = 1:N
for n = 1:N
x = N/2 - m;
y = N/2 - n;
if ((abs(x) <= R) && (abs(y) <= R))
support(m,n) = 1;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for kk = 1:Reconstructions
fprintf('Reconstruction: %d\n', kk)
ButtonHandle = uicontrol('Style', 'PushButton', ...
'String', 'Stop loop', ...
'Callback', 'delete(gcbf)');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Creating initial complex-valued field distribution at the detector plane
phase = zeros(N,N);
phase = (2*rand(N,N) - 1)*pi;
field_detector_0 = dp_amplitude(:,:).*exp(i*phase(:,:));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Getting initial object distribution
object_0 = IFT2Dc(field_detector_0);
gk = real(object_0);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Iterative loop
for ii = 1:Iterations
% fprintf('Iteration: %d\n', ii)
field_detector = FT2Dc(gk);
% Replacing updated amplitude with the measured amplitude
field_detector_updated_abs = dp_amplitude.*mask + abs(field_detector).*(1-mask);
field_detector_updated = field_detector_updated_abs.*exp(i*angle(field_detector));
% Getting updated object distribution
gk_prime = real(IFT2Dc(field_detector_updated));
error = error_function_Miao(gk_prime,support);
% Showing reconstructed object distribution
imshow(flipud(imresize(rot90(gk_prime), 0.5)), []);
title('Reconstructed object distribution')
xlabel({'x / px'})
ylabel({'y / px'})
axis on
set(gca,'YDir','normal')
colormap('gray')
colorbar;
pause(p);
% Applying constraints to the object distribution
for m = 1:N
for n = 1:N
if ((gk_prime(m,n) > 0) && (support(m,n) > 0.5))
gk1(m,n) = gk_prime(m,n);
else
gk1(m,n) = gk(m,n) - beta*gk_prime(m,n);
end
end
end
% % Treshold constraint, transmission<1 or absorption>0
% for m = 1:N
% for n = 1:N
% if ((gk1(m,n) > treshold))
% gk1(m,n) = treshold;
% end
% end
% end
gk = gk1;
if ~ishandle(ButtonHandle)
break;
end
end
phase = angle(field_detector_updated);
field_detector = sqrt(dp).*exp(i*phase);
object = real(IFT2Dc(field_detector));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Saving results
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] Latychevskaia T .Reconstruction of missing information in diffraction patterns and holograms by iterative phase retrieval[J].Optics Communications, 2019, 452:56-67.DOI:10.1016/j.optcom.2019.07.021.