题目来源：https://leetcode.cn/problems/jump-game/description/

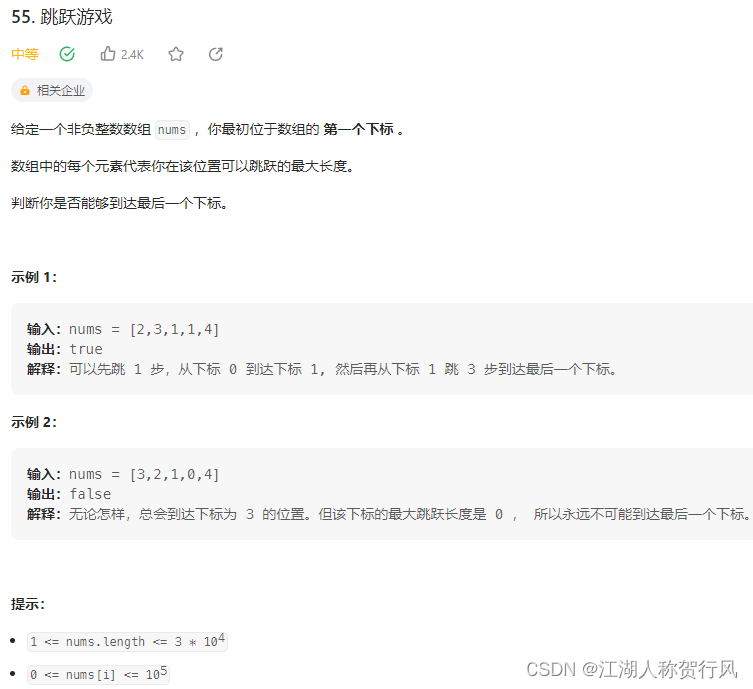
C++题解（来源代码随想录）：不断更新可覆盖范围，能达到最后一个元素即返回true，否则返回false。

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int cover = 0;
        if (nums.size() == 1) return true; // 只有一个元素，就是能达到
        for (int i = 0; i <= cover; i++) { // 注意这里是小于等于cover
            cover = max(i + nums[i], cover);
            if (cover >= nums.size() - 1) return true; // 说明可以覆盖到终点了
        }
        return false;
    }
};

贪心问题能想清楚真的很重要！