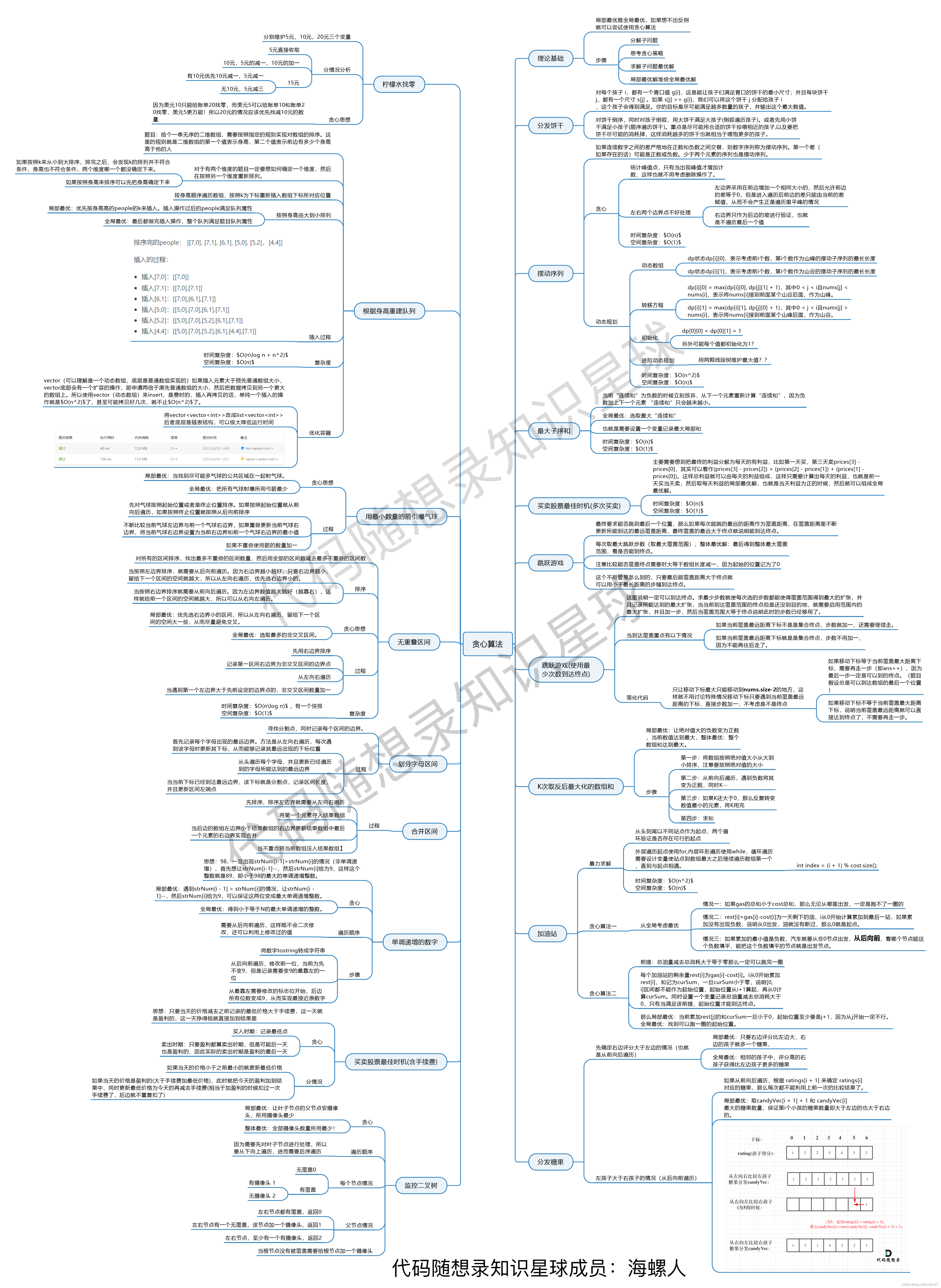
不等式

不等式在初中、高中甚至竞赛中都是比较相对综合、有难度的一块内容，经常会与方程、函数等其它知识点一起考察，一般的题型有：解不等式、证明不等式、求最大最小值。

均值不等式

均值不等式定义

一般情况下

对于任意实数a，b，有 $a^2+b^2≥2ab$ ，即 $\frac{a^2+b^2}{2}≥ab$ ，当且仅当 $a = b$ 时等号成立。
特别地，如果 $a ＞ 0 ， b ＞ 0$ ，可得 $a+b≥2\sqrt{ab}$ ，即 $\frac{a+b}{2}≥\sqrt{ab}$ 。（均值不等式），当且仅当a=b时等号成立。

（1）当 $x_1,x_2,...,x_n$ 为n个正实数时， $\frac{x_1+x_2+...+x_n}{n}≥\sqrt[n]{x_1x_2...x_n}(x_i＞0，i=1,...,n)$ ，当且仅当 $x_1=x_2=...=x_n时，等号成立。$
（2） $a+b≥2\sqrt{ab}，ab≤\frac{(a+b)^2}{4}（a,b＞0）$
（3） $a+\frac{1}{a}≥2（a＞0）$

扩展

已知两个正数a，b，则有（当且仅当a=b时取到等号）
$\frac{2}{\frac{1}{a}+\frac{1}{b}}=\frac{2ab}{a+b}≤\sqrt{ab}≤\frac{a+b}{2}≤\sqrt{\frac{a^2+b^2}{2}}$

调和平均数≤几何平均数≤算术平均数≤平方平均数

【注意】均值不等式的使用前提条件：正、定、等同时成立。
均值不等式中还有一个需要注意的地方： $a,b\in{R}$

推导加深记忆

均值不等式是由完全平方公式推导而来的

∵ $a-b)^2≥0$
∴ $a^2-2ab+b^2≥0$
∴ $a^2+b^2≥2ab$ ，这就是均值不等式了
∴ 当且仅当 $a = b$ 时等号成立
注意：a，b可以是数字，可以代数式，如单项式、多项式；整式、分式、指数式、对数式、三角式等等。如： $x+\frac{2}{x}(x＞0)，\frac{2}{x}+\frac{x}{2}(x＞0)，2^x+2^y≥2\sqrt{2^{x+y}}，log^b_a+log^a_b(log^b_a＞0)，sinx+\frac{2}{sinx}(sinx＞0)$

有公式就要用

两种用法：
一、是直接使用，形如： $x+\frac{k}{x}(k＞0)$
二、变形后再使用，有好几种，这也是难点所在
1. 负化正
2. 拆添项
3. 凑系数
4. 限定条件下的最值(常数代换，乘常数再除常数），如已知 $2 a + 3 b = 2 ， a > 0 ， b > 0$ ，求 $\frac{3}{a}+\frac{2}{b}$ 的最小值。
5. 构造 $ax+\frac{b}{x}$ 型，（此处应该联系分离常数方法，和化为部分分式的变形技巧以及对勾函数或叫耐克函数），形如 $\frac{ax^2+bx+c}{dx+e}(a,b,c,d,e为常数)$ 通过“配凑法”或“代换法”转为 $ax+\frac{b}{x}$ 型（分子上使用均值不等式）；形如 $\frac{dx+e}{ax^2+bx+c}(a,b,c,d,e为常数)$ 通过“配凑法”或“代换法”转为 $\frac{1}{ax+{\frac{b}{x}}}$ 型（分母上使用均值不等式）
6. 均值不等式失效时，需要用到对勾函数的单调性。