一、977.有序数组的平方

977.有序数组的平方
暴力法：O(NlogN) 先所有数字平方，然后再快排，时间复杂度取决于快排

class Solution
{
public:
    vector<int> sortedSquares(vector<int> &nums)
    {
        for (int i = 0; i < nums.size(); i++)
        {
            nums[i] = nums[i] * nums[i];
        }
        sort(nums.begin(), nums.end());
        return nums;
    }
};

双指针解法：O(N)

---

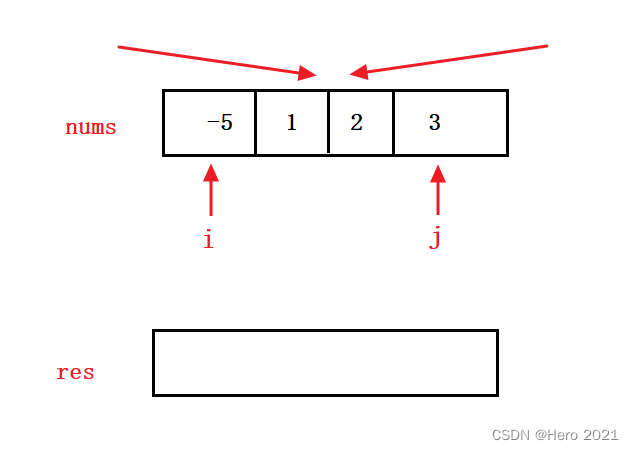
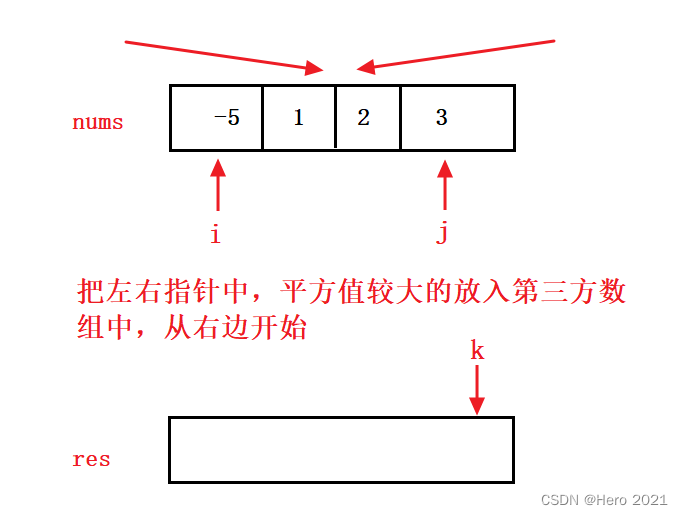
class Solution
{
public:
    vector<int> sortedSquares(vector<int> &nums)
    {
        int i = 0;
        int j = nums.size() - 1;
        int k = nums.size() - 1; // 控制res的下标，初始为最大值
        vector<int> res(nums.size(), 0);
        // 为啥取等号？i==j
        for (; i <= j;)
        {
            if (nums[i] * nums[i] > nums[j] * nums[j])
            {
                res[k] = nums[i] * nums[i];
                k--;
                i++;
            }
            else // nums[i]==nums[j]?
            {
                res[k] = nums[j] * nums[j];
                k--;
                j--;
            }
        }
        return res;
    }
};

1、为啥取等号？i==j

因为当nums[i]==nums[j]的时候循环还是要继续的，还要继续处理。

2、else 中nums[i]==nums[j]?

始终都要拿那个最大的数，去到第三方数组中，所以写在if和else中都可以。

二、209.长度最小的子数组

209.长度最小的子数组
暴力法：O(N²) 两层for循环

滑动窗口(双指针)：O(N)
使用一个for循环，做了两个for循环的事情。
j 代表的是终止位置的下标，如果代表的是起始位置，那么后边的数字依旧需要遍历，那么和暴力有啥区别呢。
滑动窗口的精华就是，如何移动起始位置？当我们发现sum >=tar的时候，意思就是起始位置到终止位置的长度是符合要求的，那么起始位置就后移一位。

class Solution
{
public:
    /*
    i 窗口的起始位置
    j 窗口的终止位置
    sum 窗口中值的和
    sublen 窗口的长度
    res 记录结果，每次更新，初值为INT_MAX
    */
    int minSubArrayLen(int tar, vector<int> &nums)
    {
        int sum = 0;
        int sublen = 0;
        int res = INT_MAX;
        for (int i = 0, j = 0; j < nums.size(); j++)
        {
            sum += nums[j];
            while (sum >= tar) // if 还是 while
            {
                sublen = j - i + 1;
                res = min(sublen, res);
                sum -= nums[i];
                i++;
            }
        }
        return res == INT_MAX ? 0 : res;
    }
};

1、if 还是 while？

我们来看一种特殊情况：

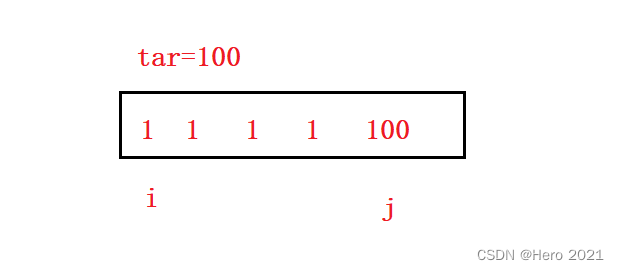
使用if只能判断一次，但是遇到特殊情况下，这个窗口需要持续变化，那么只能用while。

2、while(sum >= tar)

到达这后，便要开始更新窗口的起始位置了。

3、return res == INT_MAX ? 0 : res; —?

有可能nums中没有符合要求的子序列，返回0即可。

三、59.螺旋矩阵II

59.螺旋矩阵II
面试中经常出现
这种模拟题最简单的还是在草稿纸上画一画！！！

模拟：O(N²)

循环不变量
坚持一个规则来处理每一条边，按照左闭右开的规则

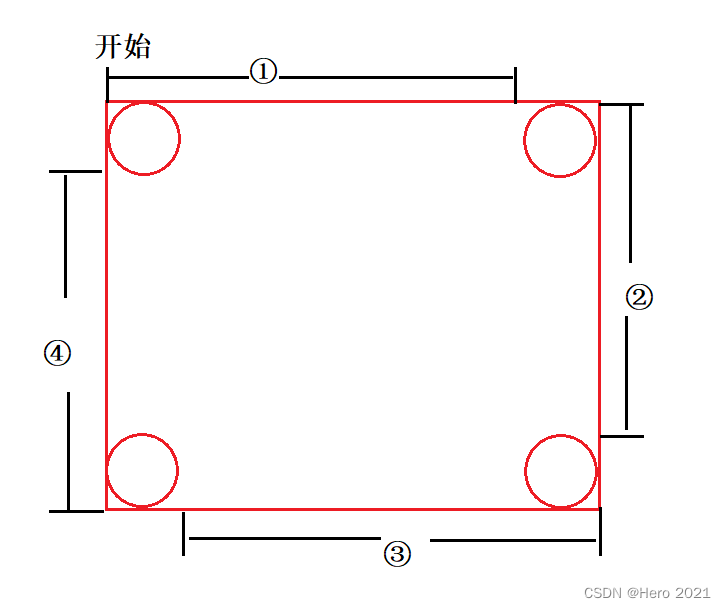
class Solution
{
public:
    vector<vector<int>> generateMatrix(int n)
    {
        vector<vector<int>> res(n, vector<int>(n, 0));
        int loop = n / 2;
        int mid = n / 2;            // 矩阵中间的位置
        int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
        int count = 1;              // 记录每个填入res中的值
        int offset = 1;             // 需要控制每一条边遍历的长度，每次循环右边界收缩一位
        int i, j;                   // 用于控制循环
        while (loop--)
        {
            // ①
            for (j = starty; j < n - offset; j++)
                res[startx][j] = count++; // 注意后置加加,行不变，列一直在+1
            // ②
            for (i = startx; i < n - offset; i++)
                res[i][j] = count++; // i在+1，j用的就是上面那行for循环剩下的j
            // ③
            for (; j > starty; j--)
                res[i][j] = count++;// i,j初始都是用的上面那行for循环剩下的作为初始值
            // ④
            for (; i > startx; i--)
                res[i][j] = count++;// i,j初始都是用的上面那行for循环剩下的作为初始值

            startx++;
            starty++;
            offset++;
        }

        // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
        if (n % 2 == 1)
        {
            res[mid][mid] = count;
        }
        return res;
    }
};

1、while(?)

我们这个循环应该转几圈呢？当n==3时我们要循环2圈，当n ==4时，要循环2圈。注意n为奇数的处理。

2、注意坐标中(x,y)与数组[i] [j]

数学坐标往右走确实变的是x,但在数组[i][j]中:向右遍历时,i不变，是j++。

3、startx++; starty++;

第二圈开始的时候，起始位置要各自加1。

4、offset++

控制每一圈里每一条边遍历的长度。