1289. 下降路径最小和 II

题目描述

给你一个 n x n 整数矩阵 grid ，请你返回 非零偏移下降路径 数字和的最小值。

非零偏移下降路径 定义为：从 grid 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。

示例 1：

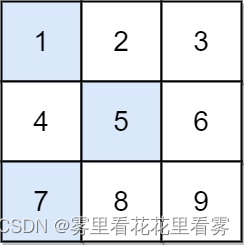
输入：grid = [[1,2,3],[4,5,6],[7,8,9]]
输出：13
解释：
所有非零偏移下降路径包括：
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ，所以答案是 13 。

示例 2：

输入：grid = [[7]]
输出：7

提示：

n == grid.length == grid[i].length
1 <= n <= 200
-99 <= grid[i][j] <= 99

解题思路

思路：下降路径最小和的变体，动态规划+优化。该题与下降路径最小和的区别是，下降路径最小和的当前元素只能由上一行左上角、正上方、右上角而来，而该题的当前元素只是不能从正上方来。最直观的想法是，加一层循环用于统计上一行的非当前列的最小值，但是这样时间复杂度就变成了O(N³)，虽然C++也能过。

int minFallingPathSum(vector<vector<int>>& grid) 
{
   int n=grid.size();
   if(n==1)
     return grid[n-1][n-1];
   //dp[i][j]表示第i行选择第j列累积的下降路径最小和
   vector<vector<long>> dp(n+2,vector<long>(n+2,0));
   //最左边和最右边两列需要赋值为INT_MAX 即不可选择对应行上的这些元素 特殊处理
   for(int k=1;k<=n;k++)
   {
     dp[k][0]=INT_MAX;
     dp[k][n+1]=INT_MAX;
   }
   long res=INT_MAX;
   for(int i=1;i<=n;i++)
   {
      for(int j=1;j<=n;j++)
      {
          long temp=INT_MAX;
          //加一层循环用于统计上一行的非当前列的最小值
          for(int k=1;k<=n;k++)
          {
             if(k!=j)
               temp=min(temp,dp[i-1][k]);
          }
          dp[i][j]=temp + grid[i-1][j-1];
          if(i==n) //最后一行 收集结果
            res=min(res,dp[i][j]);
       }
    }
    return res;
}

优化：上述O(n³)时间复杂度虽然也确实能过，但是还有优化的空间。因为在计算当前行每一个元素对应的下降路径最小和时，都需要计算一次上一行的非当前列的下降路径最小和，这样就需要计算n次，这其中有很多是重复的，所以我们需要优化此处。即思考如何一次性计算上一行的非当前列的下降路径最小和呢？计算上一行的非当前列的下降路径最小和其实可以分两个部分考虑：如果上一行的当前列不是最小值，那么直接就取上一行的最小值；如果上一行的当前列是最小值，那么就选择上一行的次小值。也就是说，对于每一行记录当前行的最小值和次小值以及最小值的下标，这样就可以为下一行所用啦，从而将计算上一行的非当前列的下降路径最小和的O(N)时间复杂度优化为O(1)时间复杂度，即整体O(N³)的时间复杂度优化为O(N²)。

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& grid) {
        //要从上一行中选出最小值，但不能和当前数字在同一列，所以要考虑到同列的情况下用次小值
        int n=grid.size();
        if(n==1)
            return grid[n-1][n-1];
        //这一行下降和的最小值 这一行最小值对应的下标 这一行的次小值
        int first_sum=0,first_pos=-1,second_sum=0;  //上一轮的
        for(int i=0;i<n;i++) 
        {
            //记录这一行的最小值、最小值对应的下标、次小值
            int fs=INT_MAX,fp=-1,ss=INT_MAX;  //用于求当前的
            for(int j=0;j<n;j++)
            {
                int cur_sum=(first_pos!=j?first_sum:second_sum)+grid[i][j];
                if(cur_sum<fs)  //找到更小的
                {
                    ss=fs;   //将更小的赋值给次小的
                    fs=cur_sum;   //将当前的赋值给最小的
                    fp=j;   //记录最小对应的位置
                }
                else if(cur_sum<ss)  //不比最小小 比次小小 更新次小
                {
                    ss=cur_sum;
                }
            }
            //为下一行做准备
            first_sum=fs;
            first_pos=fp;
            second_sum=ss;
        }
        //最后一行最小值
        return first_sum;
    }
};