题目详情：

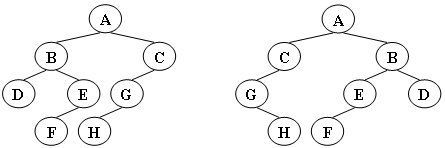
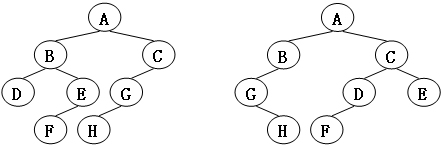
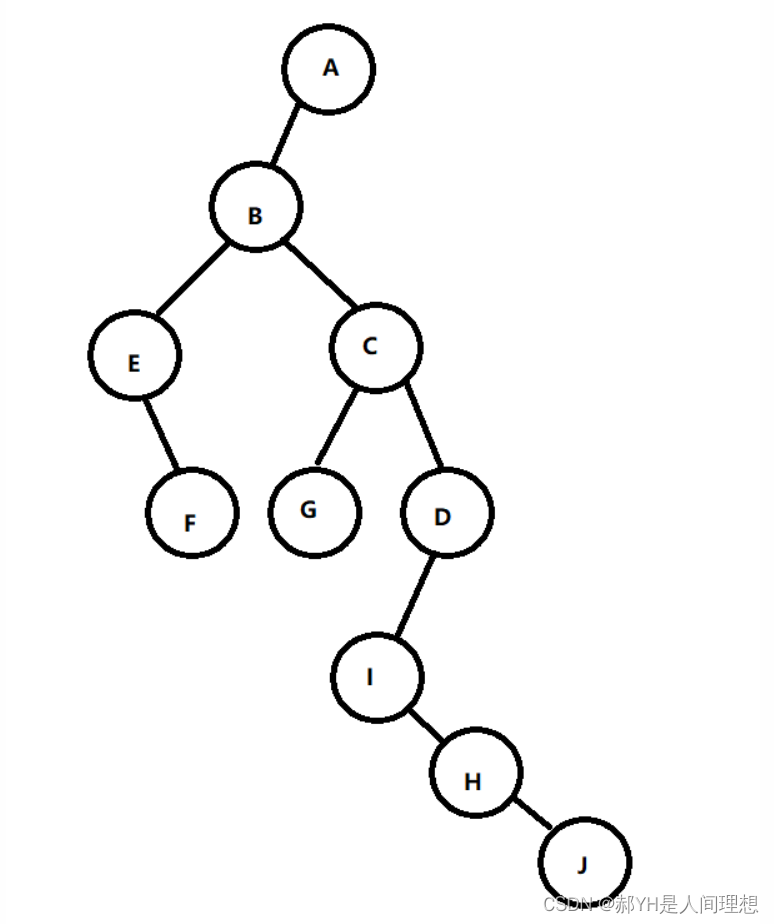
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

图1
图2

现给定两棵树，请你判断它们是否是同构的。

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

主要思路：

先要理解这句话：对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点

这句话的意思是：第i行节点编号是i，但建树时可不一定按0~n-1从左到右从上到下来建，而要根据节点关系来

难点主要分为两大部分：

（一）建树：

用一个大数组来建树，大数组的下标i对应节点i，在过程中找到根节点，扫描树时利用根节点先序遍历

（1）先初始化大数组，将每个节点存储的character设置为EMPTY，状态设置为true

（2）再遍历输入，其中处理后面子节点有讲究，应该先按字符读取，然后再判断，如果是数字，就改为数字后存入节点，否则说明子节点为空，并将子节点状态定义为false

（3）遍历大数组，其中节点character不为EMPTY且状态不为false的就是根节点

（二）判断是不是同构，用到前序遍历、递归三部曲：

（1）参数和返回值

参数：两棵树各自根节点；返回值：以当前根节点是否满足题意

（2）结束条件：

遍历到空节点

（3）遍历顺序：

前序遍历，其中的单层递归逻辑：先判断当前两个根节点是否相等，再看各自左孩子与各自右孩子是否相等，如果相等直接分别递归，如果不相等，就将第一棵子树左孩子传入下一层递归与第二棵子树右孩子比较；第一棵子树右孩子传入下一层递归与第二棵子树左孩子比较

第一次写错误：

（1）这道题有一个非常细节的点，就是如何定义表示空节点的常量NONE，当读入的符号是‘-’时，说明是空节点，如果将NONE定义为-1，那么当-1是不能用数组表示的，因为数组下标从0开始，所以因为本题数据不大(小于10），所以将最大数据MAX_SIZE定义为15，NONE定义为14（还不理解可以看代码里注释）

（2）树可能是空数，判断时要额外加一条

代码实现：

#include <stdio.h>
#include <stdbool.h>
#define MAX_SIZE 15
#define EMPTY '-'
#define NONE 14
/*定义树的数据结构*/
typedef struct TreeNode Tree;
struct TreeNode {
    char Character;
    int LeftChild;
    int RightChild;
    bool IsRoot;
};
/*建树*/
int BuildTree(int nodeNum, Tree* tree) {
    for(int i = 0; i < nodeNum; i++) {  //首先初始化树的结构体数组
        tree[i].Character = EMPTY;
        tree[i].IsRoot = true;
    }
    for(int i = 0; i < nodeNum; i++) {  //读入树的结构体数组
        char charLeftChild, charRightChild;
        scanf("%c %c %c", &(tree[i].Character), &charLeftChild, &charRightChild);
        getchar();  //读取换行符
        if(charLeftChild >= '0' && charLeftChild <= '9') {
            tree[i].LeftChild = charLeftChild - '0';
            tree[tree[i].LeftChild].IsRoot = false;
        }
        else if(charLeftChild == EMPTY) {
            tree[i].LeftChild = NONE;    //建树的这里很关键，因为树如果将NONE定义为-1，则下面tree[i].LeftChild就是-1，数组是没有-1的下标的
            tree[tree[i].LeftChild].Character = EMPTY;    //一定要有这步，因为这样在下面判断递归时才可以判断空节点（理解不了就debug）
        }
        if(charRightChild >= '0' && charRightChild <= '9') {
            tree[i].RightChild = charRightChild - '0';
            tree[tree[i].RightChild].IsRoot = false;
        }
        else if(charRightChild == EMPTY) {
            tree[i].RightChild = NONE;
            tree[tree[i].RightChild].Character = EMPTY;
        }
    }
    int rootId = -1;
    for(int i = 0; i < nodeNum; i++) {
        if(tree[i].Character != EMPTY && tree[i].IsRoot == true) {
            rootId = i;
            break;
        }
    }
    return rootId;
}
/*通过前序遍历判断是否同构*/
bool Judge(Tree* tree1, int root1, Tree* tree2, int root2) {
    //终止条件：遍历到空节点
            if(root1 == NONE && root2 == NONE) {  //两个都为空，返回true
        return true;
    }
    if((root1 == NONE && root2 != NONE) || (root1 != NONE && root2 == NONE)) {  //两个都不为空，返回false
        return false;
    }

    //前序遍历
    if(tree1[root1].Character == tree2[root2].Character) {  //如果根节点相同
        bool leftSubTree;
        bool rightSubTree;
        if(tree1[tree1[root1].LeftChild].Character == tree2[tree2[root2].LeftChild].Character &&  //左右子树对应相同
           tree1[tree1[root1].RightChild].Character == tree2[tree2[root2].RightChild].Character) {
                leftSubTree = Judge(tree1, tree1[root1].LeftChild, tree2, tree2[root2].LeftChild);
                rightSubTree = Judge(tree1, tree1[root1].RightChild, tree2, tree2[root2].RightChild);
                if(leftSubTree && rightSubTree) {
                    return true;
                }
                else return false;
        }    
        else {  //如果左右子树对应不同，就看1的左子树与2的右子树是否相同
            leftSubTree = Judge(tree1, tree1[root1].RightChild,
                                tree2, tree2[root2].LeftChild);
            rightSubTree = Judge(tree1, tree1[root1].LeftChild,
                                 tree2, tree2[root2].RightChild);
            if(leftSubTree && rightSubTree) return true;
            else return false;
        }
    }
    else return false;  //如果根节点不同不用看了，直接false
}

int main() {
    //建第一棵树
    int treeNode1;
    scanf("%d", &treeNode1);
    getchar();
    Tree tree1[MAX_SIZE];
    int root1 = BuildTree(treeNode1, tree1);

    //建第二棵树
    int treeNode2;
    scanf("%d", &treeNode2);
    getchar();
    Tree tree2[MAX_SIZE];
    int root2 = BuildTree(treeNode2, tree2);

    if(Judge(tree1, root1, tree2, root2) && treeNode1 >= 1 && treeNode2 >= 1) {
        printf("Yes");
    }
    else if(treeNode1 == 0 && treeNode2 == 0) {
        printf("Yes");
    }
    else printf("No");
    
    return 0;
}