1.线性表

什么是线性表：

线性表（linear list)是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构，常见的线性表:顺序表、链表、栈、队列、字符串...，本篇文章介绍一下顺序表。

线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储。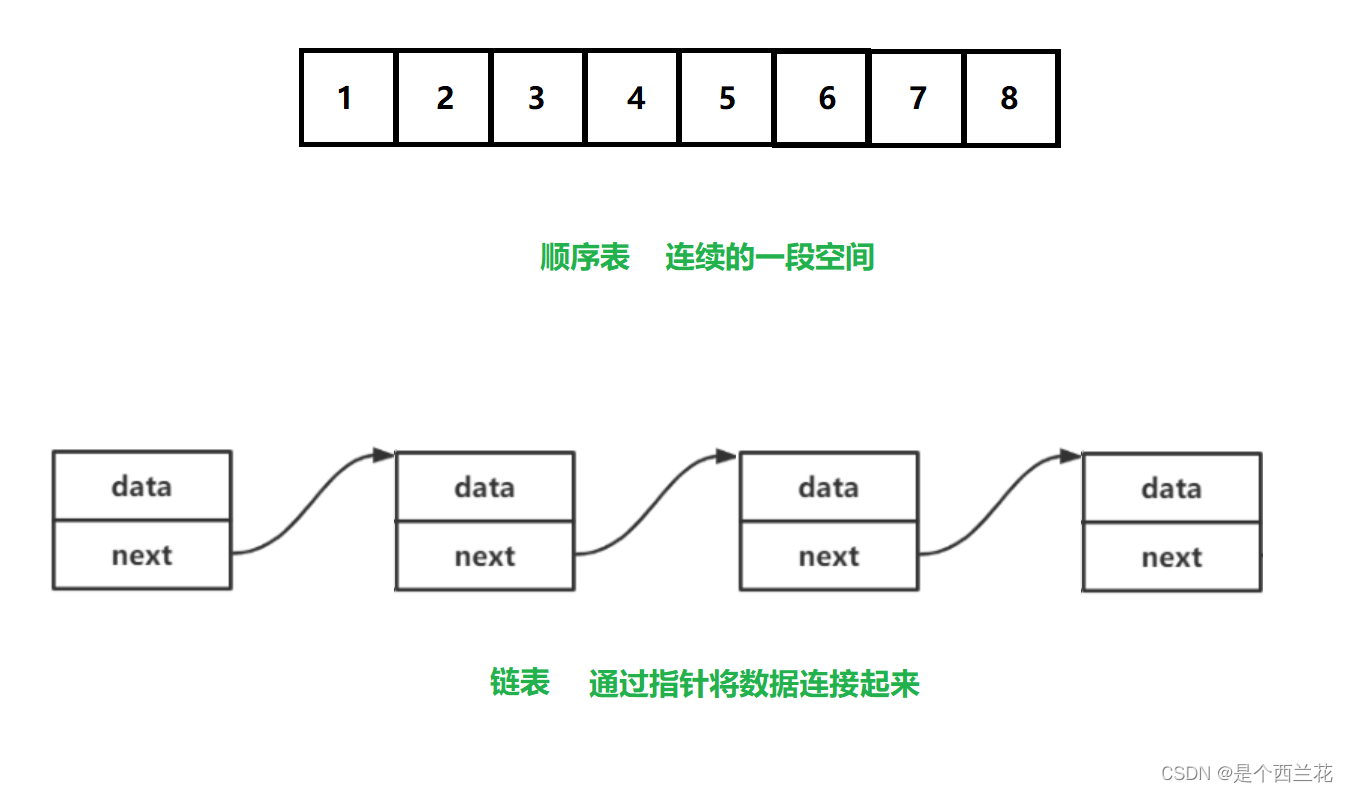

2.顺序表

2.1 概念和结构

顺序表是用一段连续的物理地址连续的存储单元依次存储数据元素，一般情况下采用数组存储。在数据上完成增删改查。

顺序表一般可以分为：

静态顺序表，使用定长数组存储元素。
动态顺序表：使用动态开辟的数组存储。

1.静态顺序表的定义

#define N 7 //顺序表的大小
typedef int SLDataType;

typedef struct SeqList
{
    SLDataType array[N];    //定长数组，顺序表只能存储N个元素
    int size;               //有效元素个数
}SeqList;

2.动态顺序表的定义

typedef int SLDatatype;

typedef struct SeqList
{
	SLDatatype* a; //指向动态开辟的数组，空间不够可以扩容
	int size;      //有效数据个数
	int capacity;  //容量空间大小
}SeqList;

2.2 接口实现

静态顺序表只适用于确定知道需要存多少数据的场景。静态顺序表的定长数组导致N定大了，空间开多了浪费，开少了不够用。

所以现实中基本都是使用动态顺序表，根据需要动态的分配空间大小，所以下面我们实现动态顺序表。

头文件：

typedef int SLDatatype;

typedef struct SeqList
{
	SLDatatype* a;
	int size;
	int capacity;
}SeqList;

//初始化
void SeqListInit(SeqList* ps);
//释放
void SeqListDestroy(SeqList* ps);
//打印
void SeListPrint(SeqList* ps);
//头插法
void SLPushfront(SeqList* ps, SLDatatype x);
//尾插法
void SLPushback(SeqList* ps, SLDatatype x);
//头删
void SLPopfront(SeqList* ps);
//尾删
void SLPopback(SeqList* ps);
//顺序表查找
int SeqListFind(SeqList* ps, SLDatatype x);
//在顺序表pos位置插入x
void SeqListInsert(SeqList* ps,int pos, SLDatatype x);
//删除顺序表pos位置的值
void SeqListErase(SeqList* ps,int pos);
//修改顺序表pos位置的值
void SeqListMidefy(SeqList* ps, int pos, SLDatatype x);

函数的实现：

//初始化
void SeqListInit(SeqList* ps)
{
	assert(ps);
	ps->a = (SLDatatype*)malloc(sizeof(SLDatatype) * 4);
	if (ps->a == 0)
	{
		perror("malloc fail");
		return;
	}
	ps->size = 0;
	ps->capacity = 4;
}
//释放
void SeqListDestroy(SeqList* ps)
{
	assert(ps);
	ps->size = 0;
	ps->capacity = 0;
	free(ps->a);
	ps->a = NULL;
}
//打印
void SeListPrint(SeqList* ps)
{
	assert(ps);
	for (int i = 0; i < ps->size; i++)
	{
		printf("%d ", ps->a[i]);
	}
	printf("\n");
}

//检查容量
int CheckCapacity(SeqList* ps)
{
	assert(ps);
	if (ps->size == ps->capacity)
	{
		SLDatatype* ptr = (SLDatatype*)realloc(ps->a, sizeof(SLDatatype) * ps->capacity * 2);
		if (ptr == NULL)
		{
			perror("realloc fail");
			return 0;
		}
		else
		{
			ps->a = ptr;
			ps->capacity *= 2;
		}
	}
	return 1;
}

//头插法
void SLPushfront(SeqList* ps, SLDatatype x)
{
	assert(ps);
	if (CheckCapacity(ps) == 0)
	{
		return;
	}

	int end = ps->size;
	while (end > 0)
	{
		ps->a[end] = ps->a[end - 1];
		end--;
	}
	ps->a[0] = x;
	ps->size++;
	
}
//尾插法
void SLPushback(SeqList* ps, SLDatatype x)
{
	assert(ps);
	if (CheckCapacity(ps) == 0)
	{
		return;
	}
	ps->a[ps->size] = x;
	ps->size++;
}
//头删
void SLPopfront(SeqList* ps)
{
	assert(ps);
	assert(ps->size > 0);
	int start = 1;
	while (start < ps->size)
	{
		ps->a[start - 1] = ps->a[start];
		start++;
	}
	ps->size--;
}
//尾删
void SLPopback(SeqList* ps)
{
	assert(ps);
	assert(ps->size > 0);
	ps->size--;
}
//顺序表查找
int SeqListFind(SeqList* ps, SLDatatype x)
{
	assert(ps);
	for (int i = 0; i < ps->size; i++)
	{
		if (ps->a[i] == x)
		{
			return i;
		}
	}
	return -1;
}
//在顺序表pos位置插入x
void SeqListInsert(SeqList* ps, int pos, SLDatatype x)
{
	assert(ps);
	assert(pos >= 0 && pos <= ps->size);
	if (CheckCapacity(ps) == 0)
	{
		return;
	}
	int end = ps->size;
	while (end > pos)
	{
		ps->a[end] = ps->a[end - 1];
		end--;
	}
	ps->a[pos] = x;
	ps->size++;
}
//删除顺序表pos位置的值
void SeqListErase(SeqList* ps, int pos)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);//已经包含 ps->size > 0
	int start = pos + 1;
	while (start < ps->size)
	{
		ps->a[start - 1] = ps->a[start];
		start++;
	}
	ps->size--;
}
//修改顺序表pos位置的值
void SeqListMidefy(SeqList* ps, int pos, SLDatatype x)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);//已经包含 ps->size > 0
	ps->a[pos] = x;
}