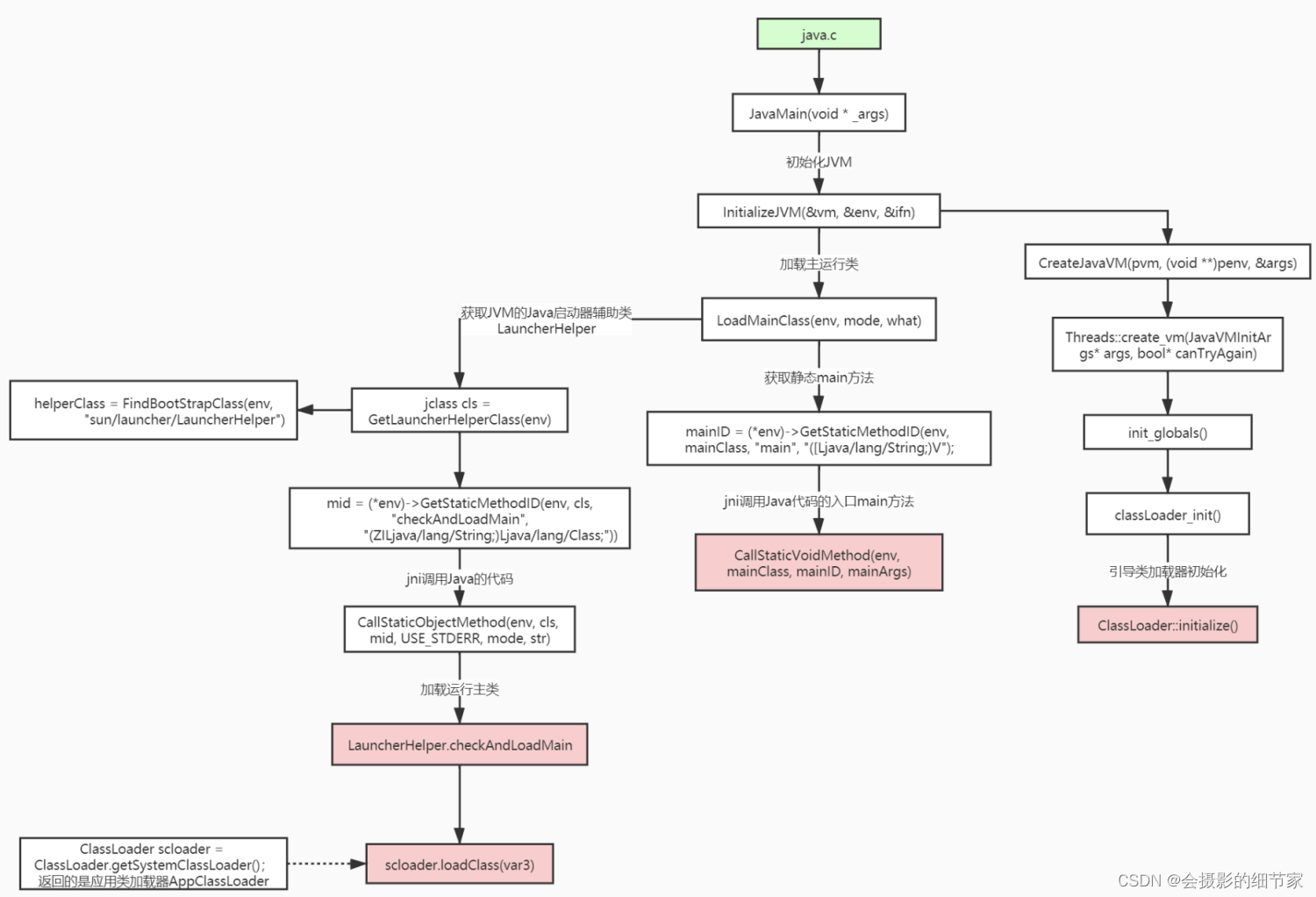
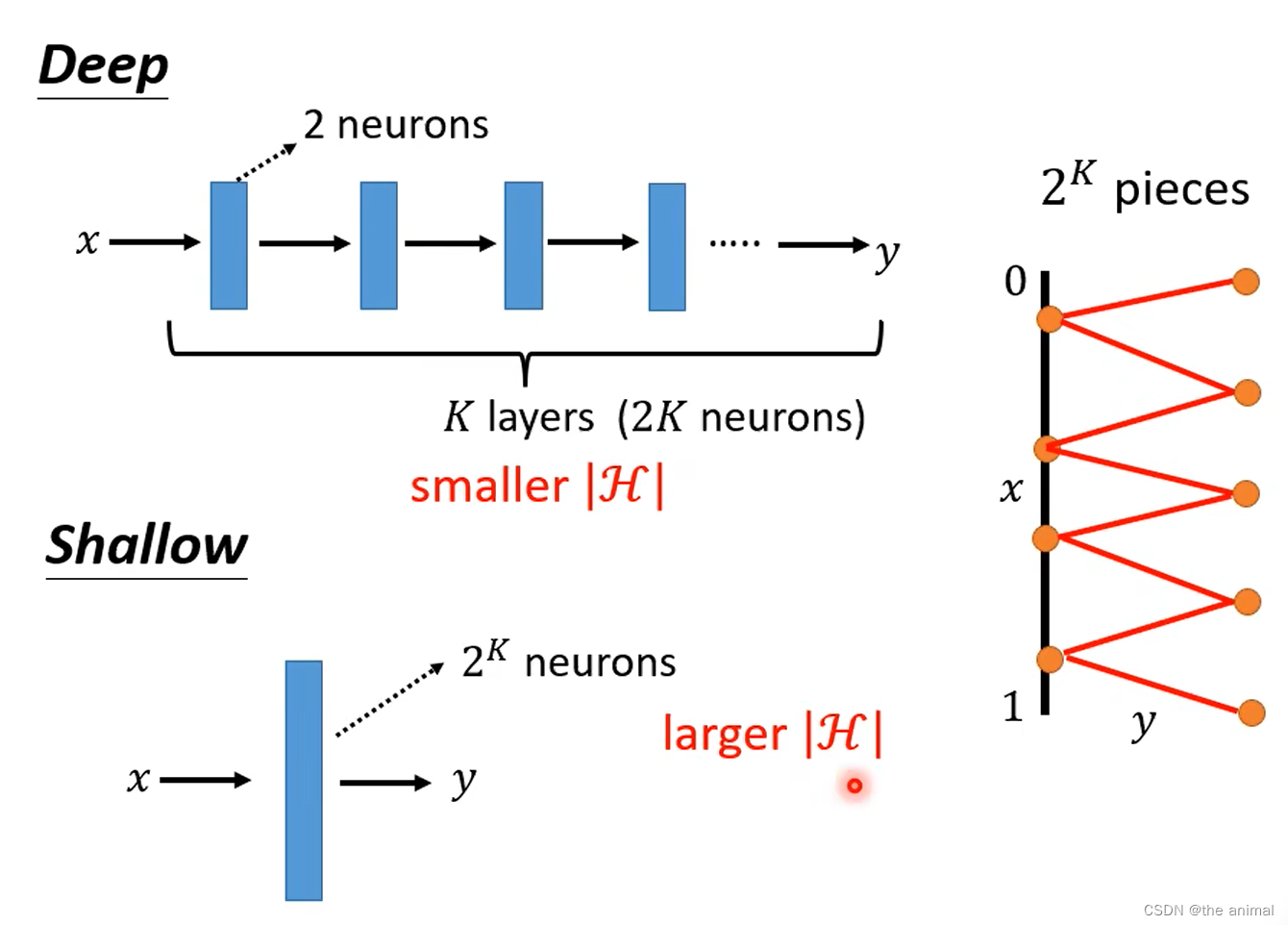
文章目录
- 1. 生成式模型简介
- 2. PixelRNN/CNN
- 3. VAE
- 3.1 自编码器AE
- 3.2 VAE基本原理
- 3.3 VAE公式推导
- 4. 参考
1. 生成式模型简介
什么是生成式模型
给定训练集,产生与训练集同分布的新样本。如下图所示,希望学习到一个模型
p
m
o
d
e
l
(
x
)
p_{model}(x)
pmodel(x),它与训练样本的分布
p
d
a
t
a
(
x
)
p_{data}(x)
pdata(x)相近

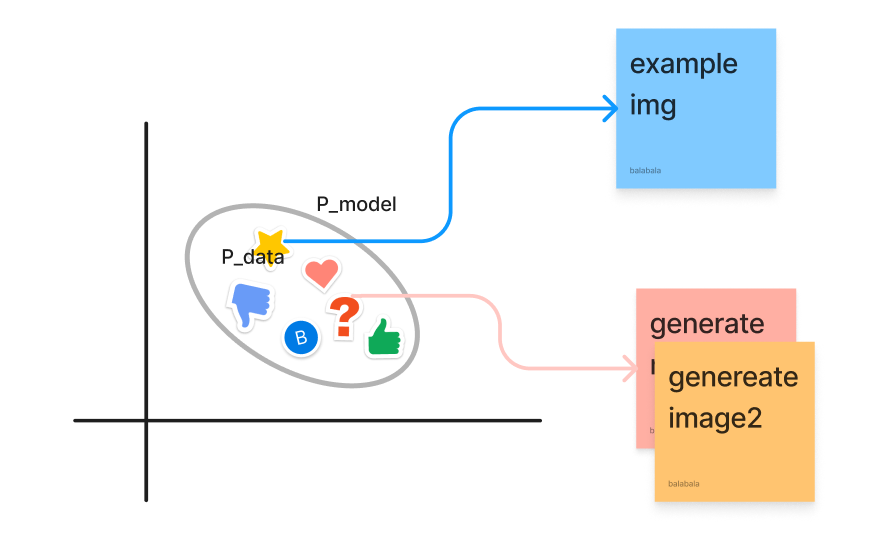
从下图可以更形象的解释,假设除了问号以外的都是真实数据,模型学习到的分布为整个椭圆以内的区域,那么从椭圆内采样任意一点(如问号)都可以生成一张对应的图片。注意其他图案对应的是真实数据,但是真实数据有限,因此通过学习一个分布就能通过采样生成无限张图片
学习拟合真实样本的的分布过程,就是无监督学习中的密度估计问题。显式的密度估计直接求出
p
model
p_{\text {model}}
pmodel的函数表达式,则可求出每个生成图像的概率;隐式的密度估计直接生成图片,无需定义表达式。
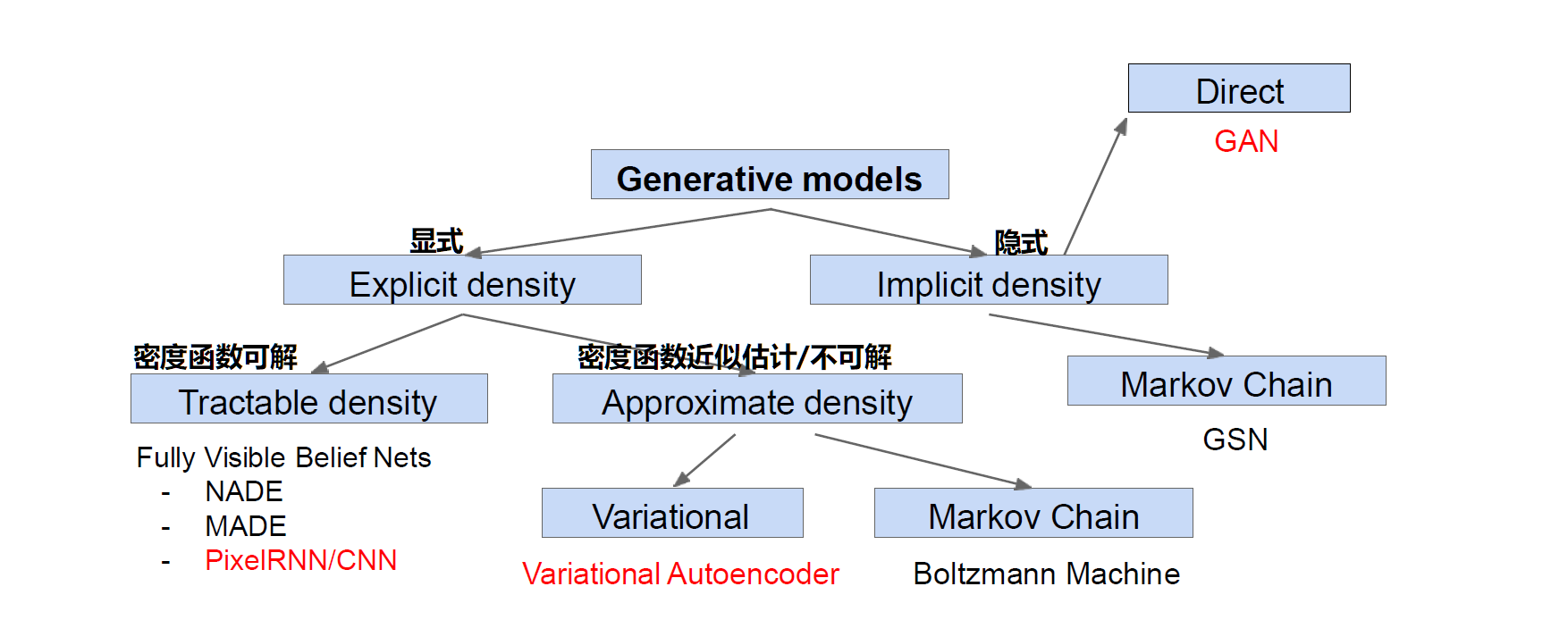
生成模型的分类
具体分类如下图所示,在本次系列文章中主要介绍PixelRNN/CNN、VAE、GAN、Diffusion
2. PixelRNN/CNN
PixelRNN
该模型是显式的密度求解。像语言模型一样,利用链式法则将图像的生成概率转变成每个像素生成概率的乘积,如下图所示,依次生成图像的每个像素

整个学习的过程就是最大化训练数据的似然,即在所有训练数据下找到一个模型使得上式概率最大。但是注意,训练数据分布是未知的(如果是高斯分布,只需直接找到
μ
\mu
μ和
δ
\delta
δ即可),分布可能很复杂,无法得知分布的表达式,这时可以使用神经网络来建模(神经网络理论上可拟合任意分布)
PixelRNN将像素生成看成一个序列生成的问题,利用RNN LSTM )的序列描述能力来生成新的像**,最大问题在于序列生成整张图片太慢了**
PixelCNN
pixelCNN依然是从图像左上角开始产生像素,基于已生成的像素,利用CNN 来生成新的像素。如下图所示在生成过程中只利用已生成的点,对未生成的点进行mask,不参加卷积运算。注意每次卷积操作输出都是一个256维向量,代表该点的每个像素值的概率

相对于pixelRNN,pixelCNN速度更快。但是依然是逐像素生成,整体仍然比较慢
3. VAE
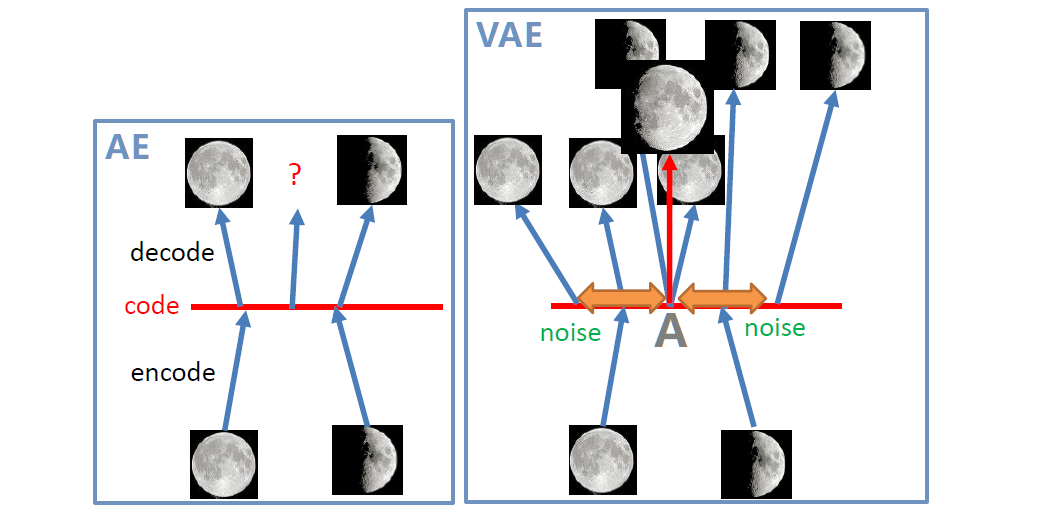
3.1 自编码器AE
自编码器是一种无监督的特征学习,其目标是利用无标签数据找到一个有效的低维特征提取器。如下图所示,其目标就是对图片进行重构,使得重构后的图像与原图尽可能相似。
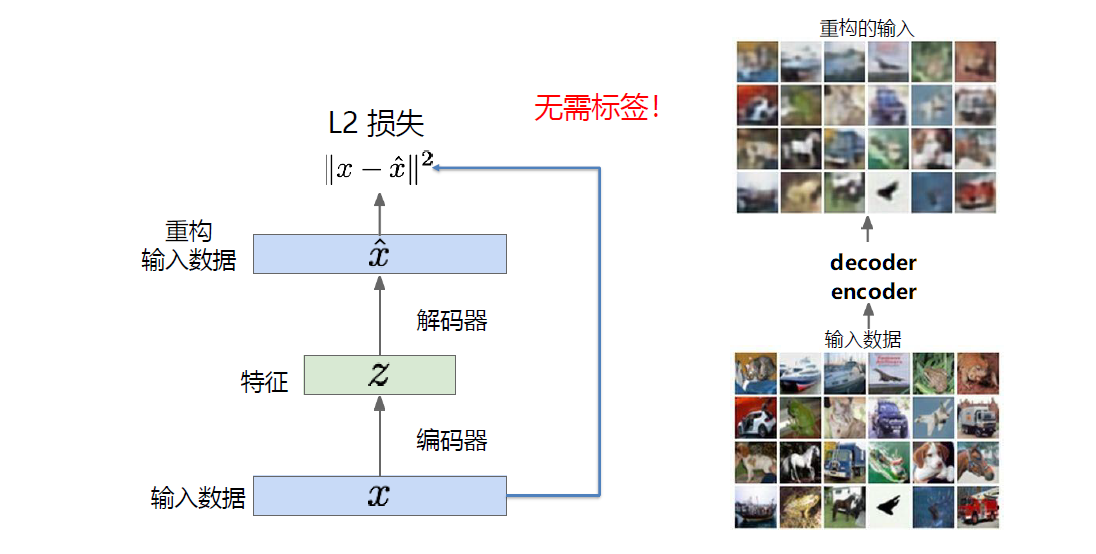
编码器用处
当自编码器训练好了后,就可以去掉解码器,并在特征
z
z
z后面接上分类等任务,进行有监督的微调学习。但是这种方式使用的仍然比较少,其效果不如直接在VGG上进行finetune。
解码器用处
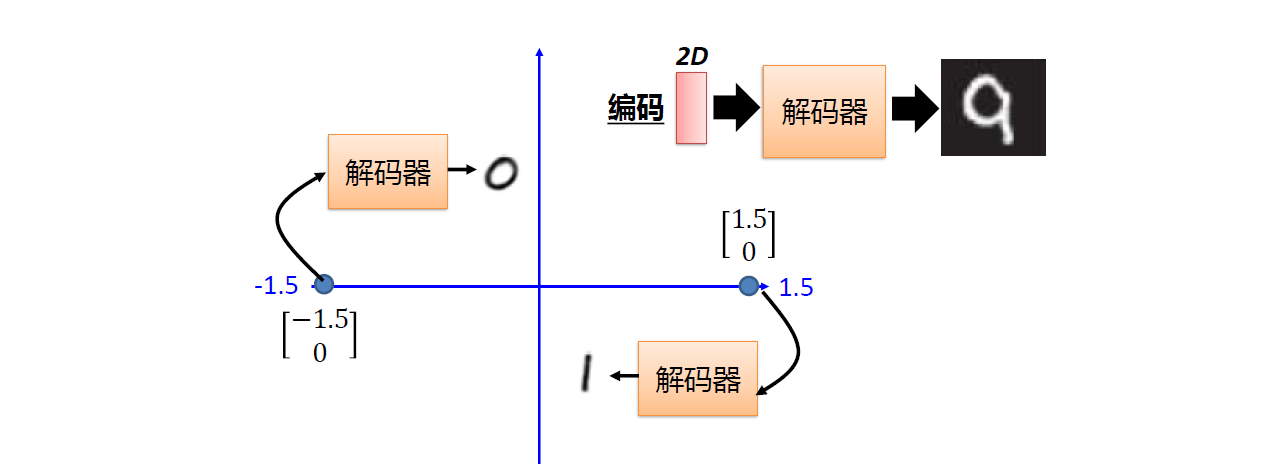
图像生成任务:如下图所示,假设训练时特征
z
z
z为2维向量,那么就可在二维空间随机采样向量,送到解码器进行图像生成
3.2 VAE基本原理
** 为什么要变分自编码器VAE **
如下图我们期望AE能在B点处生成一个介于半月核满月之间的月亮,但是自编码器从未见过B处样本,因此无法生成我们期望的月亮,它只记住了A是满月,C是半月。
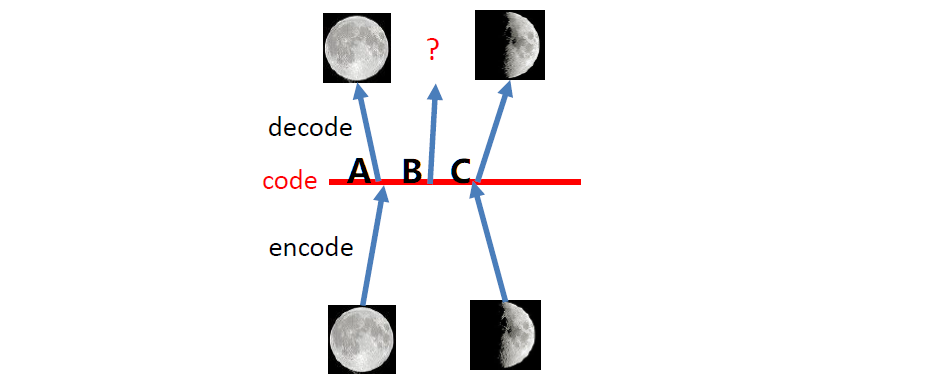
VAE基本原理
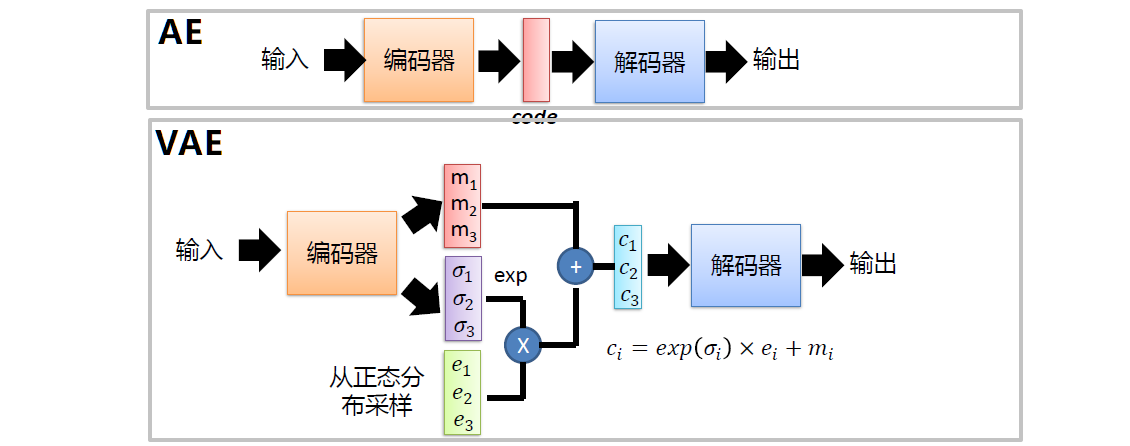
VAE的基本结构如下图所示,编码器的输出不是特征
z
z
z,而是一个分布(可以当作是一个均值为
m
m
m方差为
e
x
p
(
δ
)
exp(\delta)
exp(δ)的高斯分布)。通过重参数化技巧:高斯分布采样得到解码器的输入
c
=
e
x
p
(
δ
)
e
+
m
c=exp(\delta)e+m
c=exp(δ)e+m。
VAE的损失函数也相应的变化,不再仅仅是重构损失
∣
∣
x
−
x
^
∣
∣
2
||x-\hat x||^2
∣∣x−x^∣∣2,如果仅仅是重构损失,该模型会退化成自编码器。因此需要在重构损失后面再加上
∑
i
=
1
n
(
e
x
p
(
σ
i
)
−
(
1
+
σ
i
)
+
(
m
i
)
2
)
\sum_{i=1}^{n}(e x p(\sigma_{i})-(1+\sigma_{i})+(m_{i})^{2})
∑i=1n(exp(σi)−(1+σi)+(mi)2), 其中
m
i
2
m_i^2
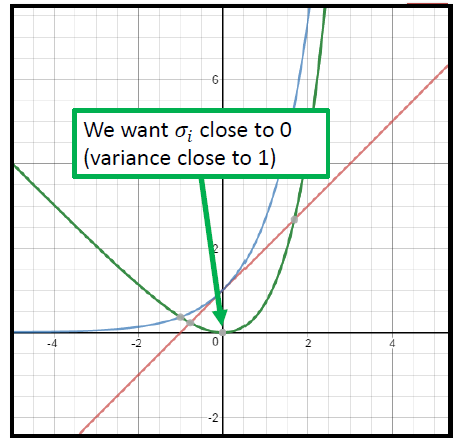
mi2是正则项,希望均值都尽可能小。而前面两项的函数图如下图所示,当
δ
\delta
δ为0时,同时让
m
m
m为0时整体最小,即让编码器输出是一个均值为0,方差为1的标准正态分布
再重新回过头来看为什么要VAE这个问题,由于VAE中有随机噪声的存在,如下图在A点处训练时既有可能生成满月,也有可能生成半月,这样最后推理时模型就学会了生成在满月和半月之间的形状。
3.3 VAE公式推导
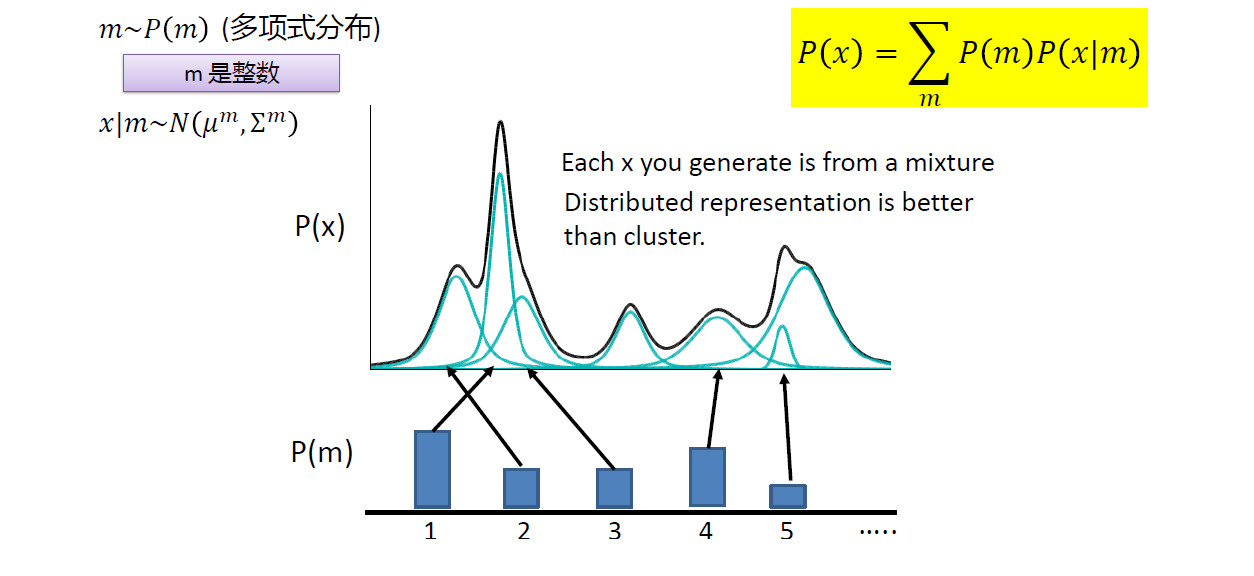
高斯混合模型
在现实中很多分布非常复杂并非是高斯分布,通常都用多个高斯分布(高斯混合模型)来表示其分布。如下图所示,黑线分布
P
(
x
)
P(x)
P(x)由多个高斯分布组成,其中
P
(
m
)
P(m)
P(m)是选择到每个子高斯分布的概率,
P
(
x
∣
m
)
P(x|m)
P(x∣m)是在第m个高斯分布里产生x的概率。
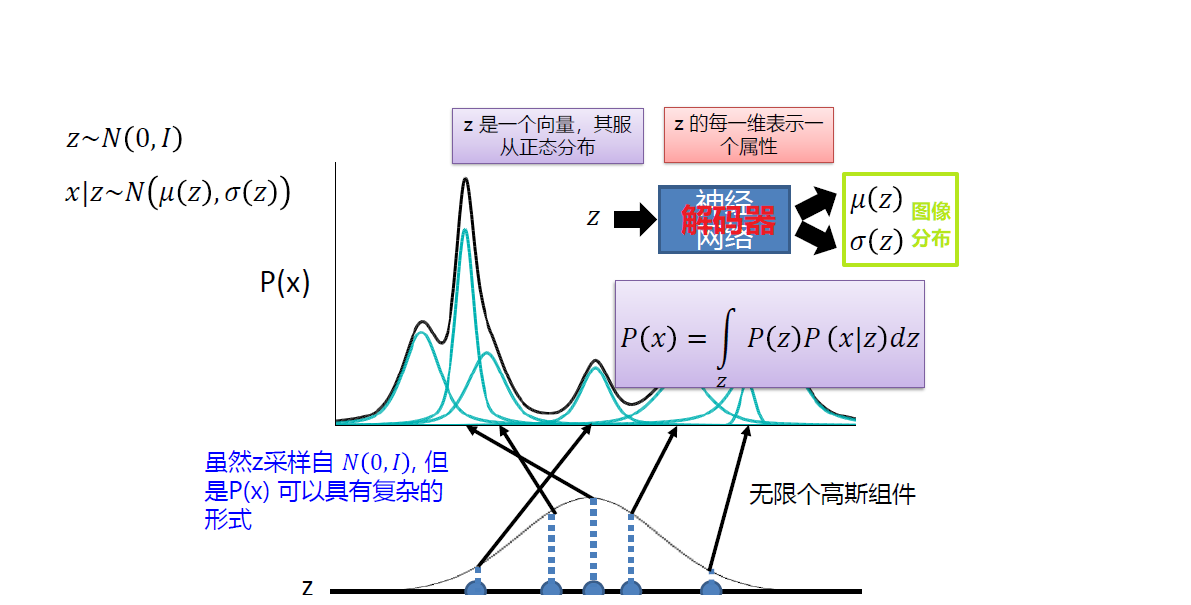
对于VAE,如下图所示,最终的图像分布
P
(
x
)
P(x)
P(x)可以看作是一个复杂的混合高斯分布,从标准正态分布中采样一个
z
z
z即可生成相应的图片,解码器的目的就是通过神经网络拟合
P
(
x
)
P(x)
P(x)
那么VAE的训练过程可看作如下图所示,最大化所有观测样本的似然。注意到,求
P
(
x
)
P(x)
P(x)时需要对
P
(
z
)
P(z)
P(z)求积分,即要穷举连续变量
z
z
z,不易实现;因此需要求另一个分布
q
(
z
∣
x
)
q(z|x)
q(z∣x),即通过给定样本获得
z
z
z,然后通过把
z
z
z送入解码器,最终通过神经网络获得图像的分布

极大似然估计过程如下图所示,(1)式中
∫
z
q
(
z
∣
x
)
d
z
=
1
\int_{z}q(z|x)d_z=1
∫zq(z∣x)dz=1,因此增加积分号对结果无影响。(2)式中使用了贝叶斯公式替换了
P
(
x
)
P(x)
P(x)

由上图可知最大化
l
o
g
P
(
x
)
logP(x)
logP(x)可以近似看作最大化下界
L
b
L_b
Lb即可,
L
b
L_b
Lb可进一步进行如下化简

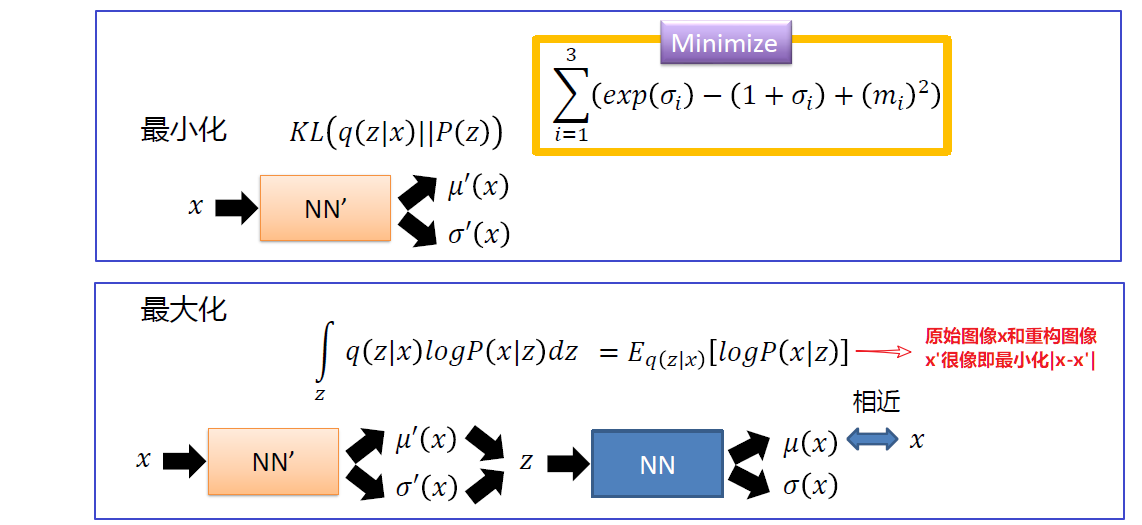
结合前面说到的损失函数,对
L
b
L_b
Lb的优化就相当于对前面提到的损失函数的优化,具体如下图所示
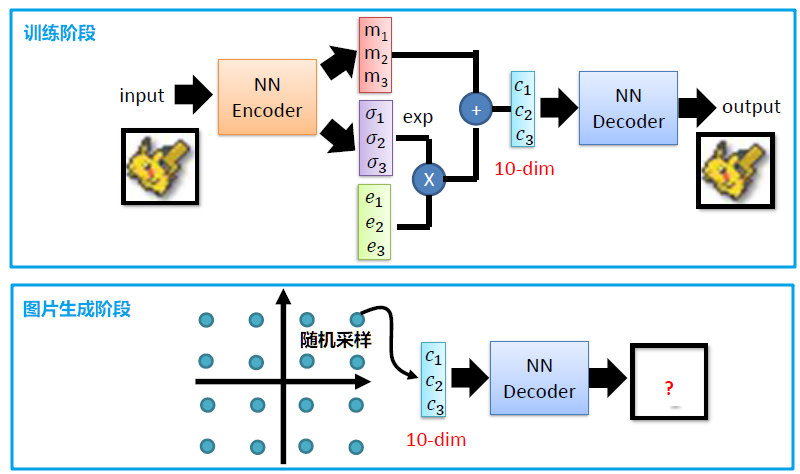
最后VAE的整体训练和应用如下图所示
4. 参考
计算机视觉与深度学习 北京邮电大学 鲁鹏


![[QT编程系列-4]:C++图形用户界面编程,QT框架快速入门培训 - 2- QT程序的运行框架:信号、槽函数、对象之间的通信](https://img-blog.csdnimg.cn/593120b7676a468d9a242ba0fd4f4584.png)