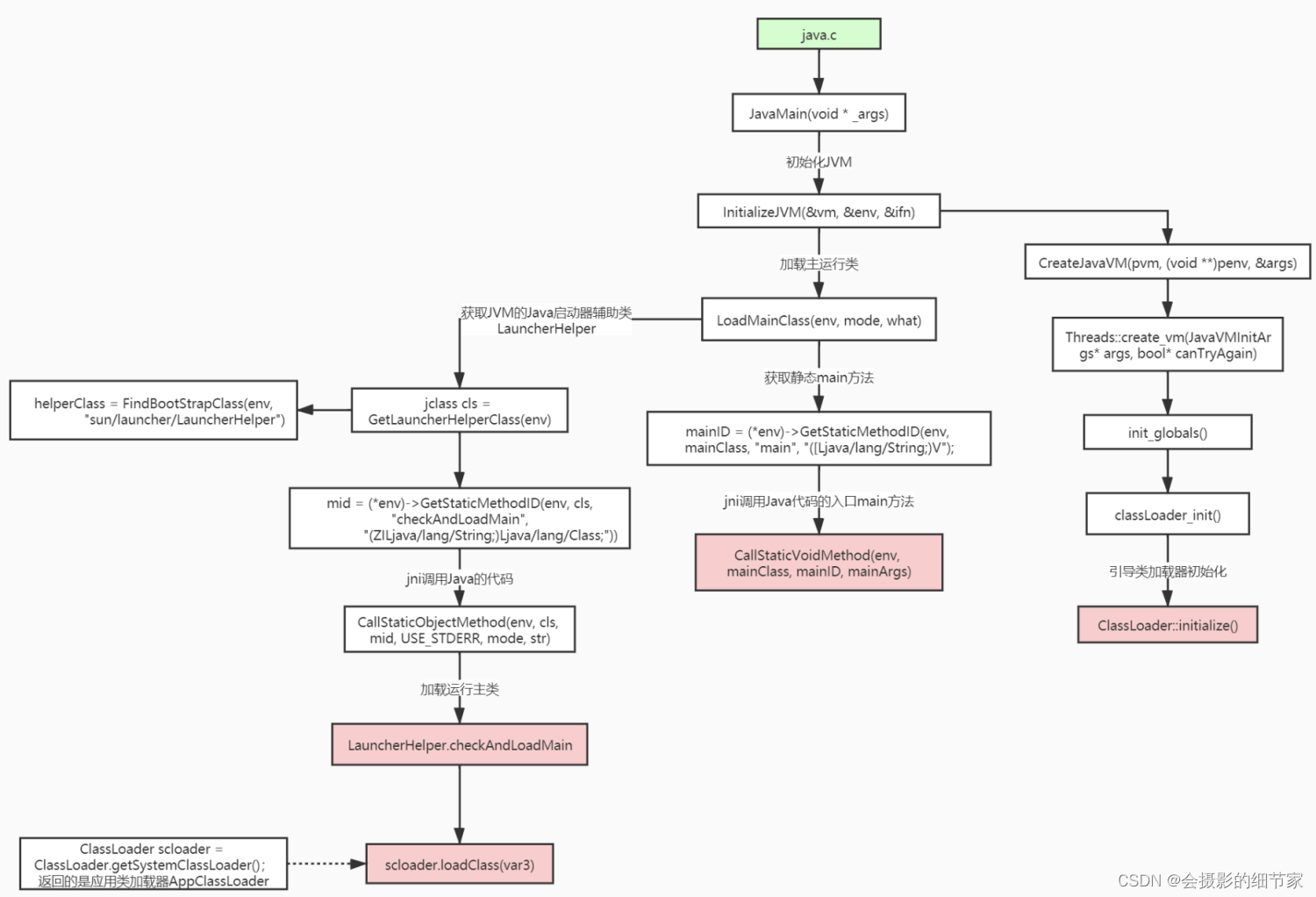
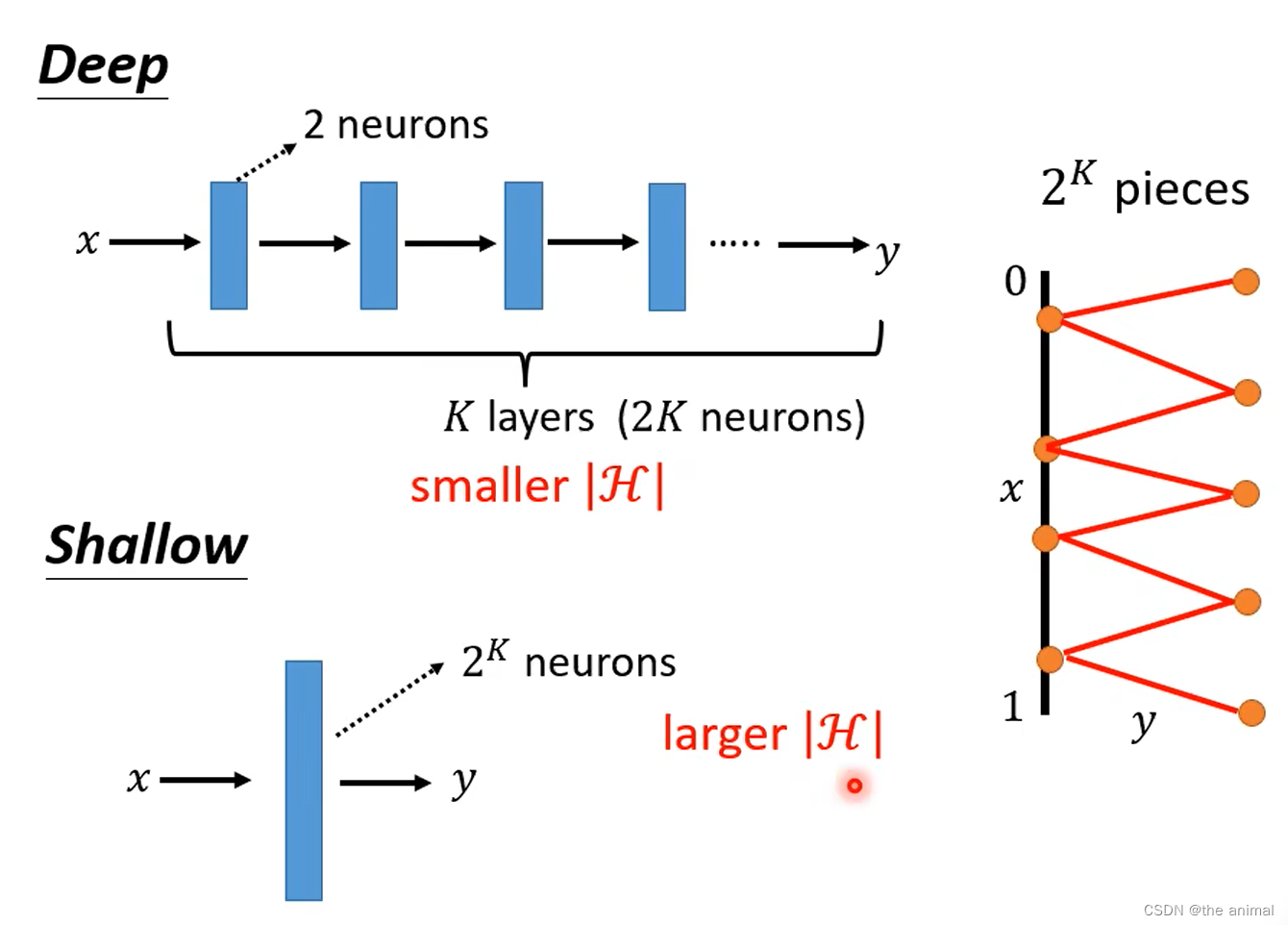
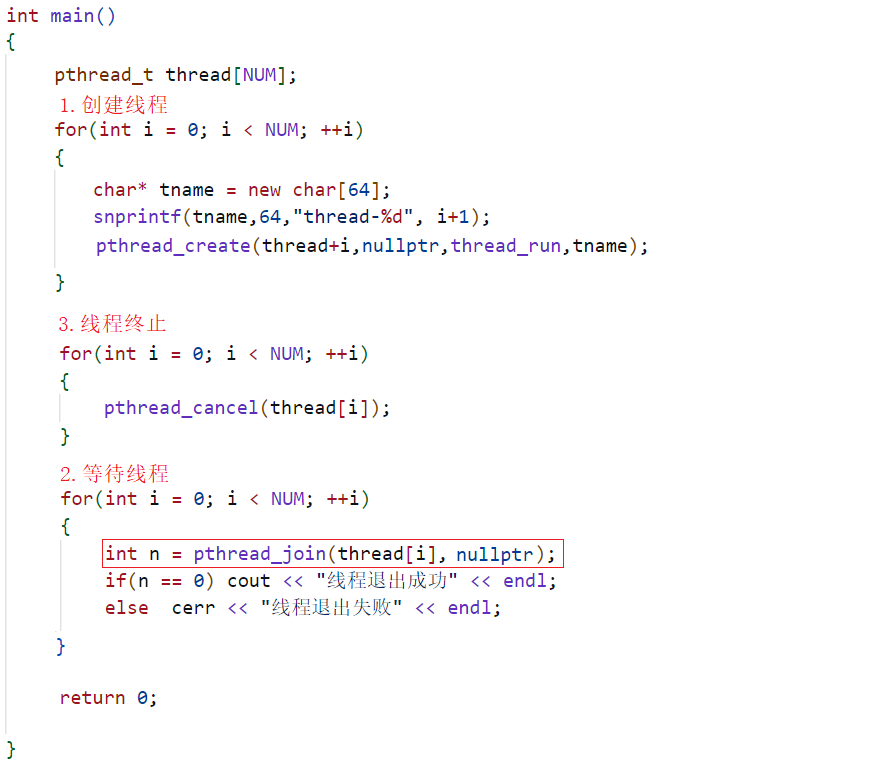
假设我们有一个简单的单层神经网络，用于解决一个简单的问题：根据一个人的年龄（x）来预测其收入（y）。在这个例子中，输入数据只有一个特征（年龄），因此我们可以用一个一维输入向量x来表示。输出结果y也是一个一维向量。

单层神经网络的结构如下：

1. 输入层：只有一个神经元，负责接收输入数据（年龄）。

2. 输出层：只有一个神经元，负责生成预测结果（收入）。

3. 连接：输入层与输出层之间的连接有一个权重w和一个偏置b。

神经网络的工作原理是：将输入数据（年龄）乘以权重w，再加上偏置b，得到预测结果（收入）。用数学公式表示为：

y = wx + b

权重求解过程如下：

1. 初始化：随机初始化权重w和偏置b的值。

2. 前向传播：将训练数据输入到神经网络中，计算预测结果y。

3. 损失计算：计算预测结果y与真实收入值之间的误差，通常采用均方误差作为损失函数，即：

   L = 1/N * ∑(yi - y'i)^2

 其中，N是训练样本数量，yi是真实收入值，y'i是神经网络预测的收入值。

4. 反向传播：根据损失函数L关于权重w和偏置b的梯度，来更新w和b的值。这里我们可以用梯度下降法来更新权重和偏置：

   w = w - α * ∂L/∂w

   b = b - α * ∂L/∂b

   其中，α是学习率，用于控制权重更新的速度。

5. 迭代：重复执行步骤2至4，直到损失函数L收敛到一个较小的值，或达到预设的迭代次数。

通过这个过程，我们可以找到一组合适的权重w和偏置b，使得神经网络能够根据年龄来预测收入。最后，当我们有一个新的年龄值x时，可以将其输入到神经网络中，计算出对应的收入预测值y。