一 排序算法
1.1 冒泡法排序
-
冒泡排序(Bubble Sort)是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。
-
首先从数组的第一个元素开始到数组最后一个元素为止,对数组中相邻的两个元素进行比较,如果位于数组左端的元素大于数组右端的元素,则交换这两个元素在数组中的位置。这样操作后数组最右端的元素即为该数组中所有元素的最大值。接着对该数组除最右端的n-1个元素进行同样的操作,再接着对剩下的n-2个元素做同样的操作,直到整个数组有序排列。
1.2 时间复杂度
冒泡法的时间复杂度为O(n^2)。
1.3 稳定性
冒泡法排序是一种稳定的算法
算法稳定性:假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
1.4 实现
#include <stdio.h>
void bubble_sort(int arr[], int len) {
int i, j, temp;
for (i = 0; i < len - 1; i++)
for (j = 0; j < len - 1 - i; j++)
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
int main() {
int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
int len = (int) sizeof(arr) / sizeof(*arr);
bubble_sort(arr, len);
int i;
for (i = 0; i < len; i++)
printf("%d ", arr[i]);
return 0;
}1.2 选择排序
1.2.1 基本逻辑
选择排序的基本思想描述为:
-
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
-
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
-
重复第二步,直到所有元素均排序完毕。
1.2.2 时间复杂度
选择排序的时间复杂度为O(n^2)。
1.2.3 稳定性
选择排序是一种不稳定的算法
1.2.4 实现
void swap(int *a,int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
void selection_sort(int arr[], int len)
{
int i,j;
for (i = 0 ; i < len - 1 ; i++)
{
int min = i;
for (j = i + 1; j < len; j++)
if (arr[j] < arr[min])
min = j;
swap(&arr[min], &arr[i]);
}
}1.3 插入排序
1.3.1 基本逻辑
-
插入排序的基本思想就是将无序序列插入到有序序列中。
-
插入排序的的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
-
步骤:
-
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
-
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
-
-
图示:
-
第一轮: 从第二位置的 6 开始比较,比前面 7 小,交换位置。
-
1.3.2 时间复杂度
插入排序的时间复杂度为O(n^2)。
1.3.3 稳定性
插入排序是稳定的排序算法
1.3.4 实现
void insertion_sort(int arr[], int len){
int i,j,key;
for (i=1;i<len;i++){
key = arr[i];
j=i-1;
while((j>=0) && (arr[j]>key)) {
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}1.4 快速排序
1.4.1 基本逻辑
-
快速排序的基本思想是:通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,已达到整个序列有序。
-
快速排序是一种分治法。
-
一趟快速排序的具体过程可描述为:
-
从数列中挑出一个元素,称为 "基准"(pivot);
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
-
1.4.2 时间复杂度
平均时间复杂度为
1.4.3 稳定性
快排法是一种不稳定的排序算法。
1.4.4 实现
一趟快速排序的具体做法为:设置两个指针low和high分别指向待排序列的开始和结尾,记录下基准值baseval(待排序列的第一个记录),然后先从high所指的位置向前搜索直到找到一个小于baseval的记录并互相交换,接着从low所指向的位置向后搜索直到找到一个大于baseval的记录并互相交换,重复这两个步骤直到low=high为止。
// 快速排序
void QuickSort(int arr[], int start, int end)
{
if (start >= end)
return;
int i = start;
int j = end;
// 基准数
int baseval = arr[start];
while (i < j)
{
// 从右向左找比基准数小的数
while (i < j && arr[j] >= baseval)
{
j--;
}
if (i < j)
{
arr[i] = arr[j];
i++;
}
// 从左向右找比基准数大的数
while (i < j && arr[i] < baseval)
{
i++;
}
if (i < j)
{
arr[j] = arr[i];
j--;
}
}
// 把基准数放到i的位置
arr[i] = baseval;
// 递归
QuickSort(arr, start, i - 1);
QuickSort(arr, i + 1, end);
}1.5 归并排序
1.5.1 基本逻辑
-
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。
-
“归并”的含义是将两个或两个以上的有序序列组合成一个新的有序表。假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列的长度为1,然后两两归并,多个有序子序列,再两两归并。如此重复,直到得到一个长度为n的有序序列为止。这种排序方法称为2-路归并排序。
1.5.2 时间复杂度
归并排序的时间复杂度是O(n㏒n)。
但是,归并排序的空间复杂度是O(n)。
1.5.3 稳定性
归并排序是稳定的算法,它满足稳定算法的定义。
1.5.4 实现
#include<stdio.h>
#define ArrLen 20
void printList(int arr[], int len) {
int i;
for (i = 0; i < len; i++) {
printf("%d\t", arr[i]);
}
}
void merge(int arr[], int start, int mid, int end) {
int result[ArrLen];
int k = 0;
int i = start;
int j = mid + 1;
while (i <= mid && j <= end) {
if (arr[i] <= arr[j]){
result[k++] = arr[i++];
}
else{
result[k++] = arr[j++];
}
}
if (i == mid + 1) {
while(j <= end)
result[k++] = arr[j++];
}
if (j == end + 1) {
while (i <= mid)
result[k++] = arr[i++];
}
for (j = 0, i = start ; j < k; i++, j++) {
arr[i] = result[j];
}
}
void mergeSort(int arr[], int start, int end) {
if (start >= end)
return;
int mid = ( start + end ) / 2;
mergeSort(arr, start, mid);
mergeSort(arr, mid + 1, end);
merge(arr, start, mid, end);
}
int main()
{
int arr[] = {4, 7, 6, 5, 2, 1, 8, 2, 9, 1};
mergeSort(arr, 0, 9);
printList(arr, 10);
system("pause");
return 0;
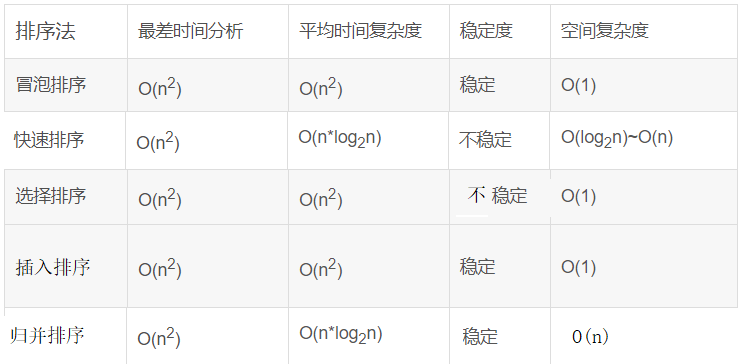
}1.6 常用排序算法总结
二、查找算法
2.1 二分查找法
2.1.1 基本逻辑
二分查找(Binary Search),也叫做折半查找,是一种在有序数组中查找某一特定元素的查找算法。查找过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则查找过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。
这种查找算法每一次比较都使查找范围缩小一半。
{5,13,19,21,37,56,64,75,80,88,92}采用折半查找算法查找关键字为 21 的过程为:
-
找到中间值
-
21比中间值小,则在左半部分找中间值
-
比中间值大,则在右半部分找中间值
2.1.2 时间复杂度
折半查找每次把搜索区域减少一半,时间复杂度为 O(logn) 空间复杂度:O(1)
2.1.3 实现
递归实现:
#include<stdio.h>
#define SIZE 10
typedef int ElemType;
int refind(ElemType *data,int begin,int end,ElemType num);
int main(void){
ElemType data[SIZE]={10,20,30,40,50,60,70,80,90,100};
ElemType num;
for(int i = 0;i<SIZE;i++)
printf("%d ",data[i]);
printf("\n请输入要查找的数据:\n");
scanf("%d",&num);
int flag = refind(data,0,SIZE,num);
printf("位置为:%d\n",flag);
return 0;
}
/
//递归
int refind(ElemType *data,int begin,int end,ElemType num)
{
if(begin > end)
{
printf("没找到\n");
return -1;
}
int mid = (begin+end)/2;
if(data[mid] == num)
{
return mid;
}else if(data[mid] <= num)
return refind(data,mid+1,end,num);
else
return refind(data,begin,mid-1,num);
}非递归实现:
#include <stdio.h>
int bin_search( int str[], int n, int key )
{
int low, high, mid;
low = 0;
high = n-1;
while( low <= high )
{
mid = (low+high)/2;
if( str[mid] == key )
{
return mid; // 查找成功
}
if( str[mid] < key )
{
low = mid + 1; // 在后半序列中查找
}
if( str[mid] > key )
{
high = mid - 1; // 在前半序列中查找
}
}
return -1; // 查找失败
}
int main()
{
int str[11] = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89};
int n, addr;
printf("请输入待查找的关键字: ");
scanf("%d", &n);
addr = bin_search(str, 11, n);
if( -1 != addr )
{
printf("查找成功, 关键字 %d 所在的位置是: %d\n", n, addr);
}
else
{
printf("查找失败!\n");
}
return 0;
}2.2 不使用排序查找数组中第二大的值
2.2.1 思路
-
定义最大值max初始化为a[0],第二大值为sec,遍历数组,如果数组元素比max大就更新,max=a[i],sec记录上一次max的值;
-
如果数组元素不大于max,再将数组元素和sec判断,如果数组元素a[i]大于sec,则更新sec,sec=a[i]
2.2.2 代码实现
int secondbig(int data[],int N)
{
int max=data[0],sec=0;
for(int i=1;i<N;i++)
{
if(max<data[i])
{
sec=max;
max=data[i];
}
else
{
if(data[i]>sec)
{
sec=data[i];
}
}
}
return sec;
}
int main()
{
int a[]={12,34,45,3,15,7,6,10};
int sec = secondbig(a,8);
return 0;
}