说明

闵老师的文章链接： 日撸 Java 三百行（总述）_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护：https://github.com/fulisha-ok/sampledata

通用BP神经网络之激活函数

1. 激活函数

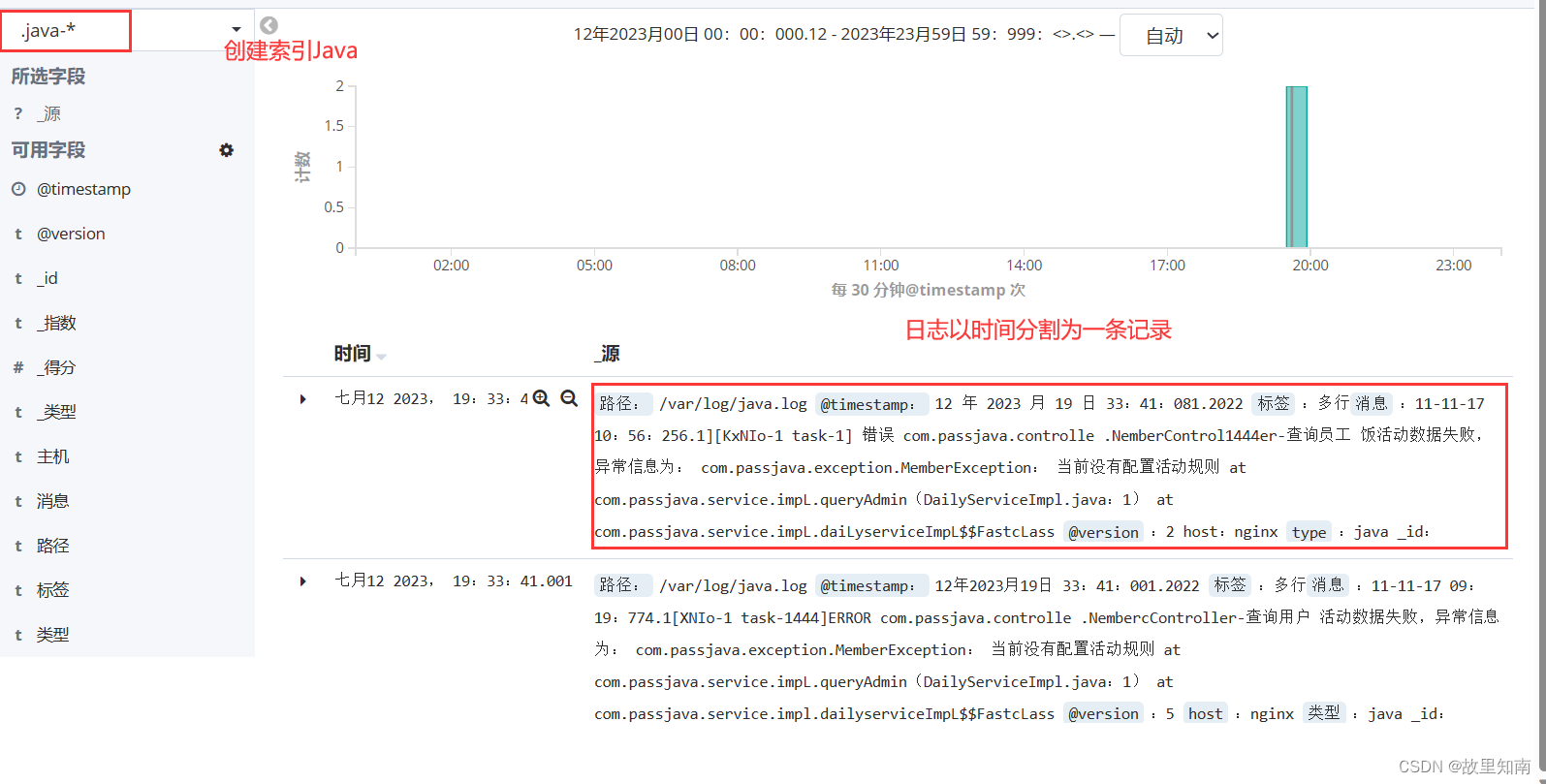
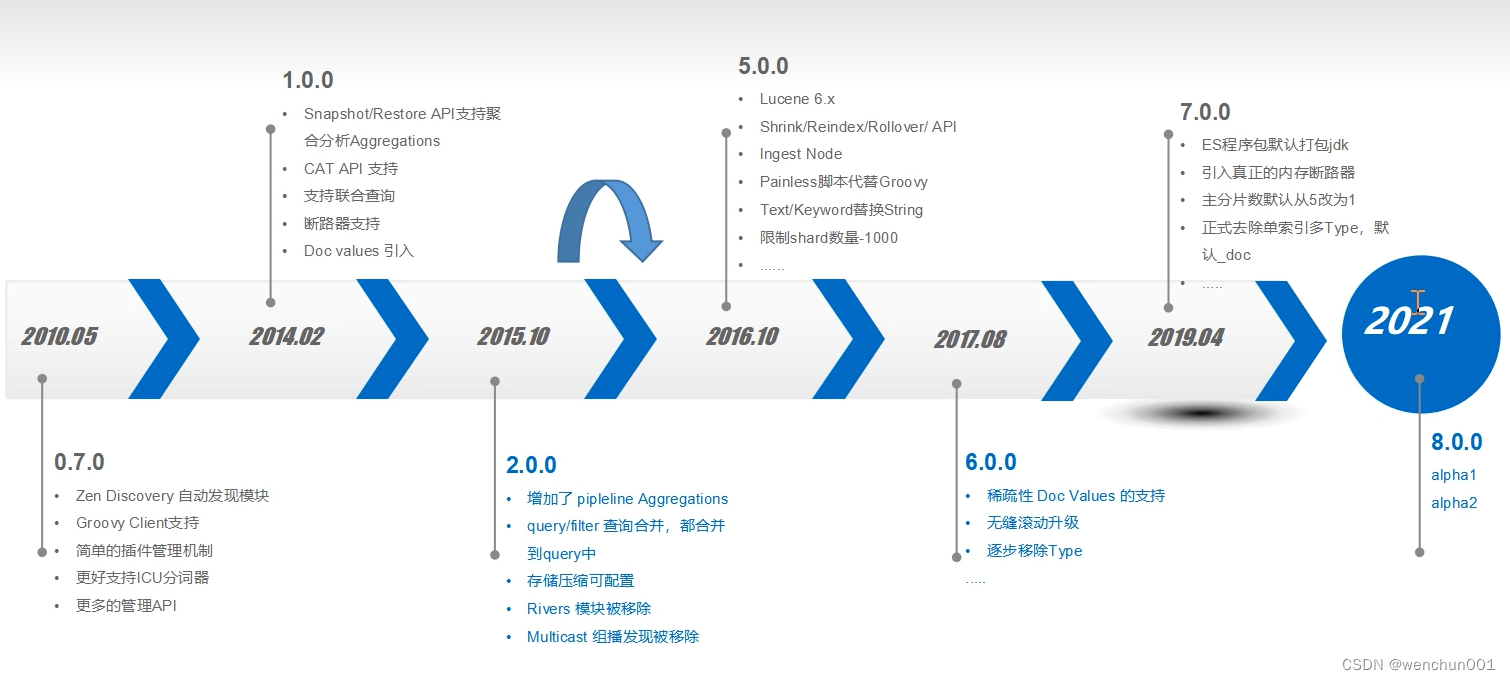
激活函数就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端(百度百科的解释)即可以理解为在神经网络的每个层中，激活函数对输入信号进行处理，并生成输出信号

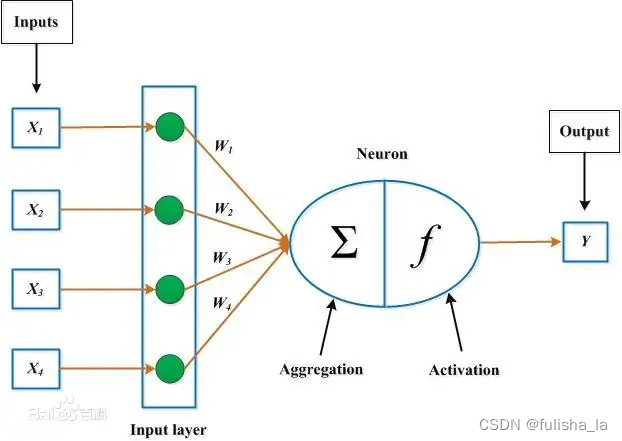
上面这张图应该不陌生，我在上一篇文章中也用到过。
激活函数大多数都是非线性函数(通过下面的图像也可以感受到)，通过使用非线性激活函数，神经网络可以引入非线性特性，从而使得网络能够学习和表示更加复杂的函数关系（但这句话就我目前来说我不能很深刻的理解）

2. 激活函数分类

随着学习会慢慢增加

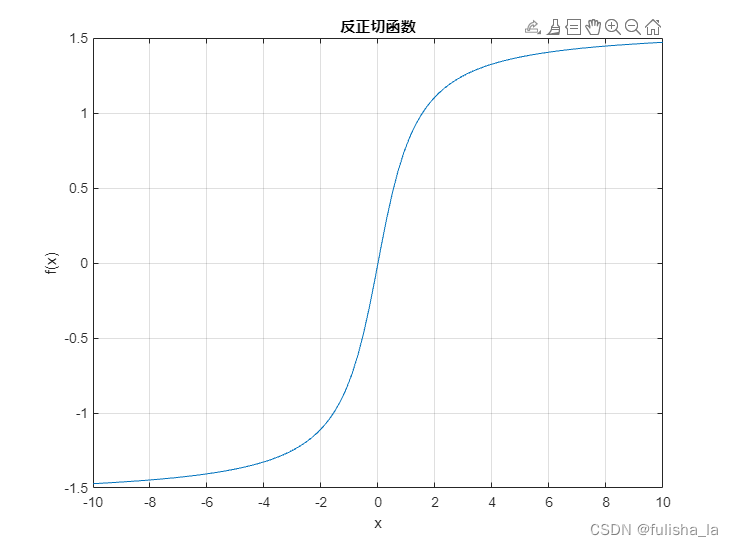
1.1 反正切函数（ArcTan）

• 公式
  $$f(x)=ta{n}^{-1}(x)$$
  $$f^{\prime }(x)=\frac{1}{1+x^2}$$
• 图像
  

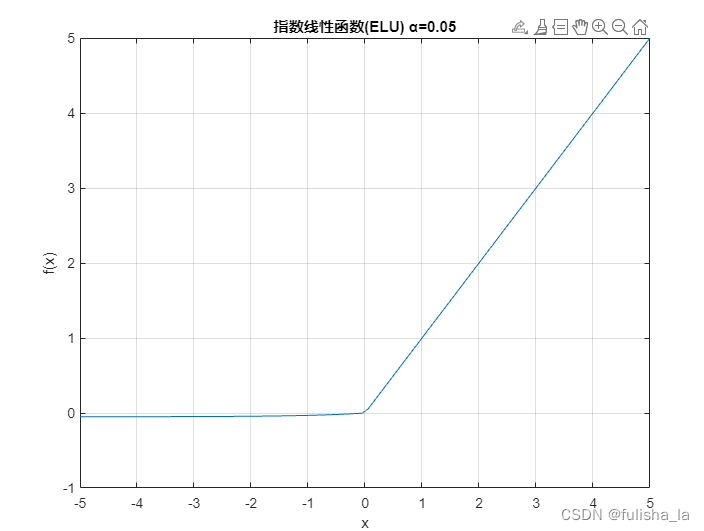
1.2 指数线性函数（ELU）

$$f(x)=\{\begin{array}{ll}\alpha (e^x-1),& x<0\\ x,& x\ge 0\end{array}$$
$$f^{\prime }(x)=\{\begin{array}{ll}\alpha e^x,& x<0\\ 1,& x\ge 0\end{array}$$

• 图像
  

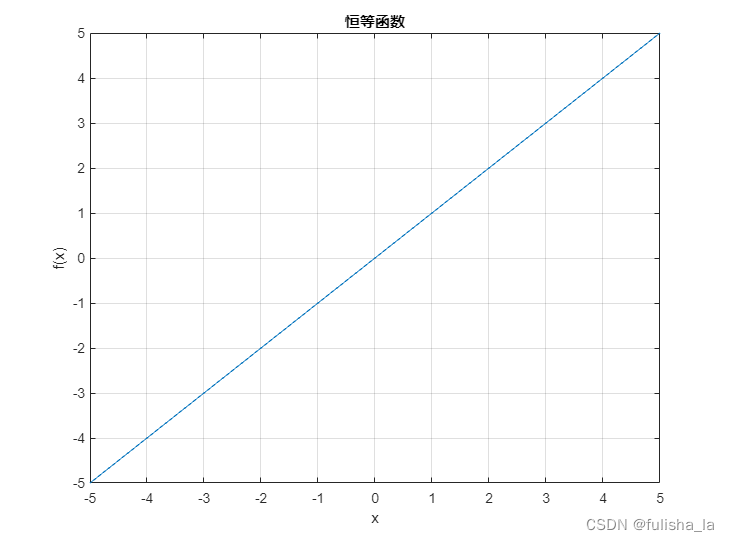
1.3 恒等函数

• 公式
  $$f(x)=x$$
  $$f^{\prime }(x)=1$$
• 图像
  

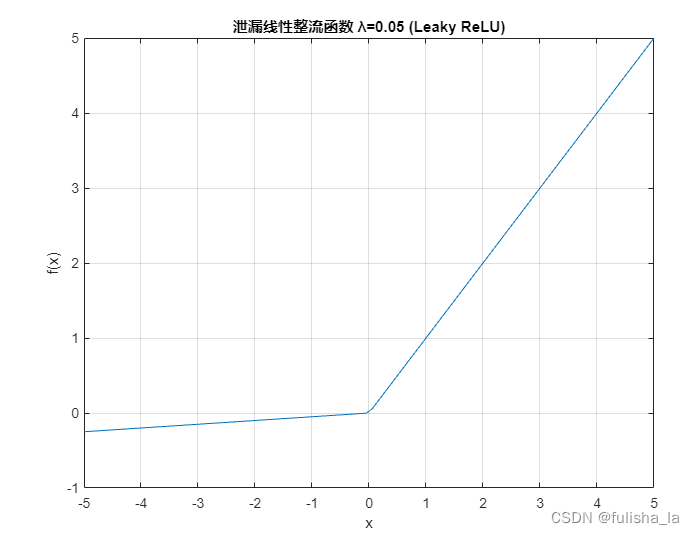
1.4 泄漏线性整流函数(LEAKY_RELU)

$$f(x)=\{\begin{array}{ll}\lambda x,& x<0\\ x,& x\ge 0\end{array}$$
$$f^{\prime }(x)=\{\begin{array}{ll}\lambda ,& x<0\\ 1,& x\ge 0\end{array}$$

• 图像
  

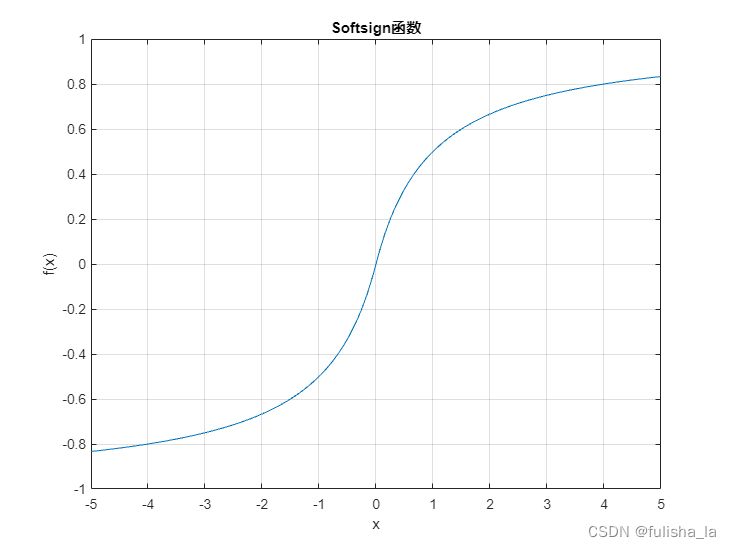
1.5 softsign

• 公式
  $$f(x)=\frac{1}{1+|x|}$$
  $$f^{\prime }(x)=\{\begin{array}{ll}\frac{1}{(1+x{)}^2},& x\ge 0\\ \frac{1}{(1-x{)}^2},& x<0\end{array}$$
• 图像
  

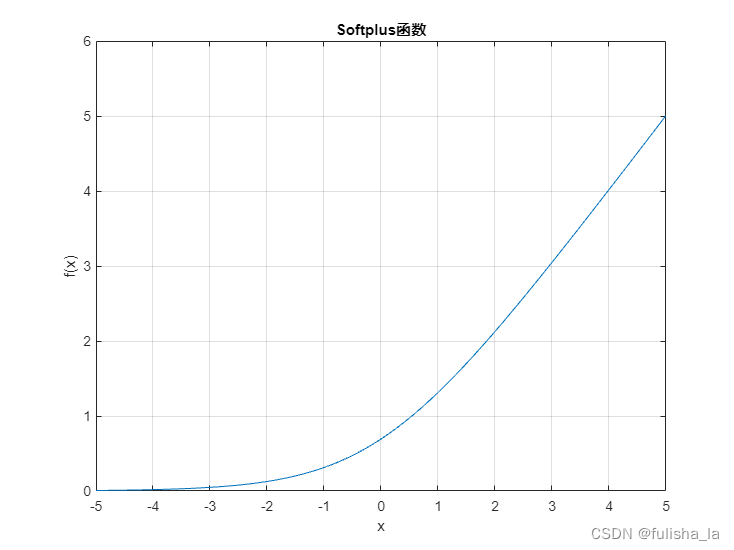
1.6 softplus

• 公式
  $$f(x)=\log (1+e^x)$$
  $$f^{\prime }(x)=\frac{1}{1+e^{-x}}$$
• 图像
  

1.7 Relu函数

• 公式
  $$f(x)=max(0,x)$$
  $$f^{\prime }(x)=\{\begin{array}{ll}1,& x\ge 0\\ 0,& x<0\end{array}$$

• 图像
  

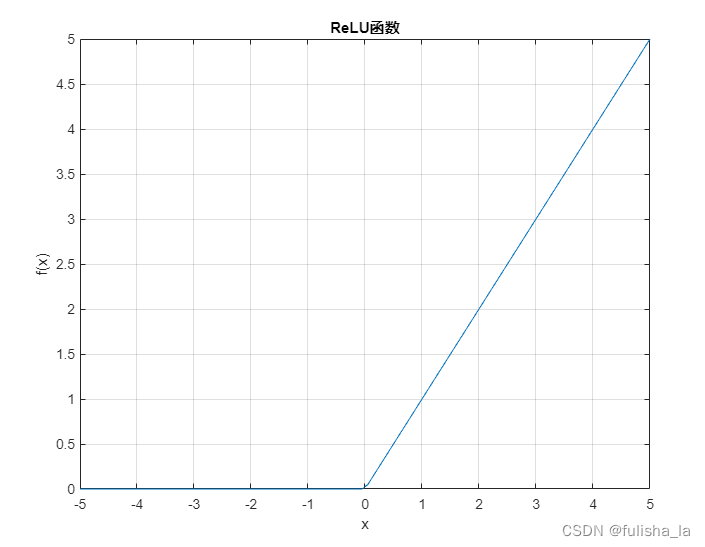
1.8 sigmoid函数

• 公式
  $$f(x)=\frac{1}{1+e^{-x}}$$
  $$f^{\prime }(x)=\frac{e^{-x}}{(1+e^{-x}{)}^2}=f(x)(1-f(x))$$
• 图像
  

1.9 双曲正切函数（tanh）

• 公式
  $$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
  $$f^{\prime }(x)=1-f(x{)}^2$$
• 图像
  

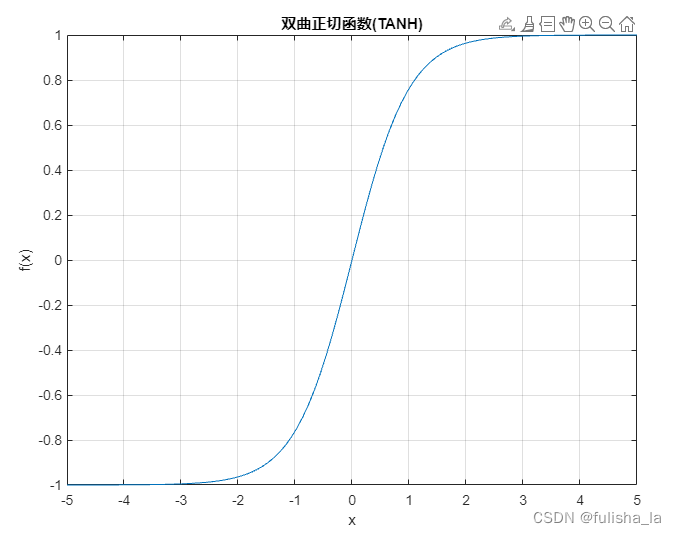
1.10 Binary step函数

• 公式
  $$f(x)=\{\begin{array}{ll}1,& x\ge 0\\ 0,& x<0\end{array}$$

• 图像
  

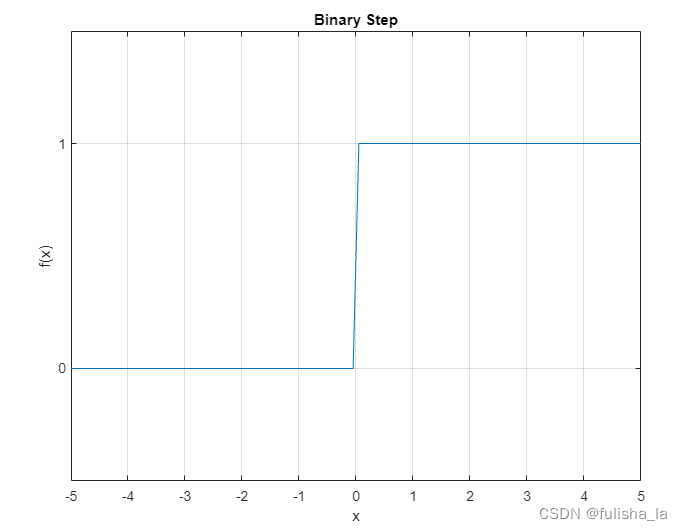
1.11 ISRU函数

• 公式
  $$f(x)=\frac{x}{\sqrt{1+\alpha x^2}}$$
  $$f^{\prime }(x)=(\frac{1}{\sqrt{1+\alpha x^2}}{)}^3$$
• 图像
  

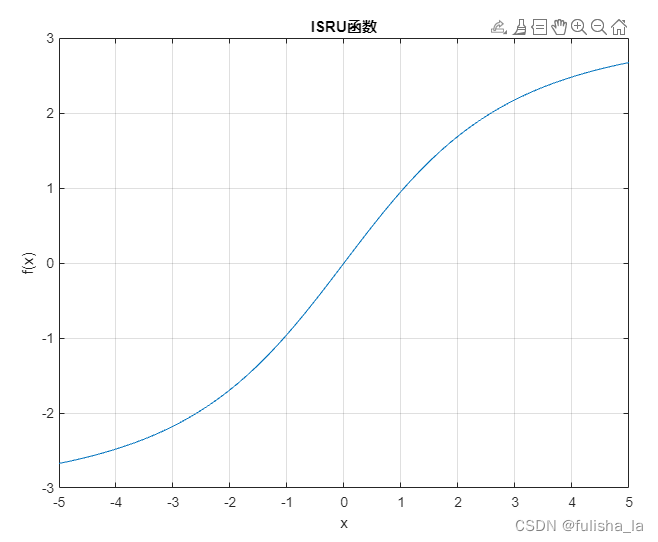
1.12 Swish函数

$$f(x)=\frac{x}{1+e^{-kx}}=x\ast Sigmoid(kx)$$

$$f^{\prime }(x)=kf(x)+Sigmoid(kx)(1-kf(x))$$

• 图像