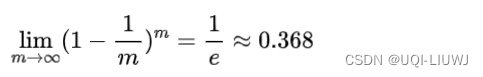1 集成学习
- 集成学习通过构建多个学习器采用加权的方式来完成学习任务
- 一般来讲,多个学习器同属于一种模型,比如决策树,线性模型,而不会交叉用多种模型
- 为了保证集成学习的有效性,多个弱分类器之间应该满足两个条件
- 准确性:个体学习器要有一定的准确性,这样才能有好的效果
- 多样性:学习器之间要有一些差异,完全相同的几个学习器集成起来后几乎不会有提升
2 随机森林
- 随机森林是集成学习中Bagging方式的代表
- 采样多组训练集,并行训练弱分类器
- 相对于决策树而已,有一个很重要的优点:防止过拟合
- 防止过拟合的方式与Dropout有点类似
- 随机选择样本作为训练集(Bootstrap Sampling)
- 训练集中特征随机选择
- 防止过拟合的方式与Dropout有点类似
2.1 Bootstrap Sampling
- Bootstrap Sampling 是一种统计学上的采样方法
- 对于有m个样本的数据集D,进行m次有放回采样得到数据集D'
- 这样D与D'的大小一致。
- 有放回采样使得中D'有的样本重复出现,有的样本则没有出现
- 某个样本在m次采样中使用没有被采到的概率为
- 当m趋近于∞时
- ——>D中样本差不多63.2%在D'中
- 当m趋近于∞时
- 用这种方式采样B个样本集
- 对这B个样本集分别训练一个基学习器
- 对这B个样本集分别训练一个基学习器
2.2 决策
决策时,在分类任务中通常采用投票法,若两个类别票数一样,最简单的做法是随机选择一个;
而回归任务则一般使用平均法

2.3 基学习器和随机森林
- 早期的Bagging方法是每个基学习器都是一个决策树,完全按照决策树的规则建树
- 随机森林则在Bagging的基础继续采用特征随机,每个基学习器只对在k个特征构成的子集下进行建树
- 随机选择k个特征
- 一般k=logd
- ——>这样构建的决策树相对于完整的决策树是一个“浅决策树”,这样就构成了特征的随机性
3 随机森林的偏差和方差(bias,variance)
- 因为基学习器相同,因此各个学习器有近似的Bais和Variance
- bias
- Variance
- 如果各个基学习器独立
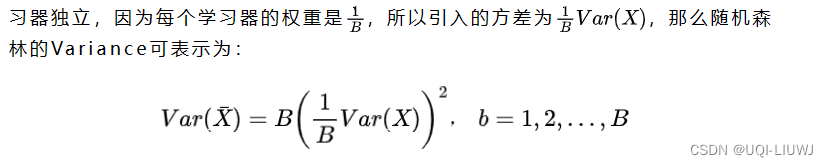
- Bagging通过降低Variance来防止过拟合
- 严格来说每个学习器之间不严格独立,所以Variance的降低会小于B倍
参考内容:【机器学习】随机森林 (qq.com)