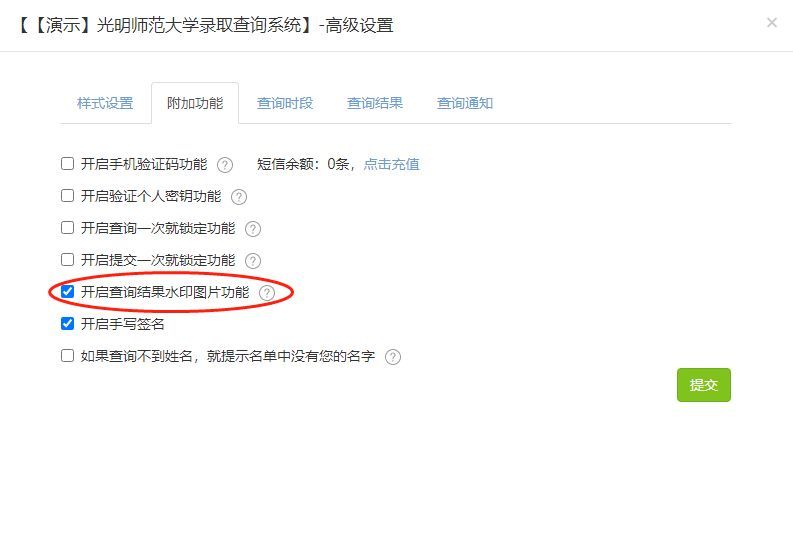
A 最长交替子序列

暴力枚举
class Solution {
public:
int alternatingSubarray(vector<int> &nums) {
int n = nums.size();
for (int len = n; len > 1; len--) {
for (int i = 0; i + len - 1 < n; i++) {
int j = i + 1;
for (; j < i + len; j++)
if (nums[j] - nums[j - 1] != ((j - i) % 2 ? 1 : -1))
break;
if (j == i + len)
return len;
}
}
return -1;
}
};
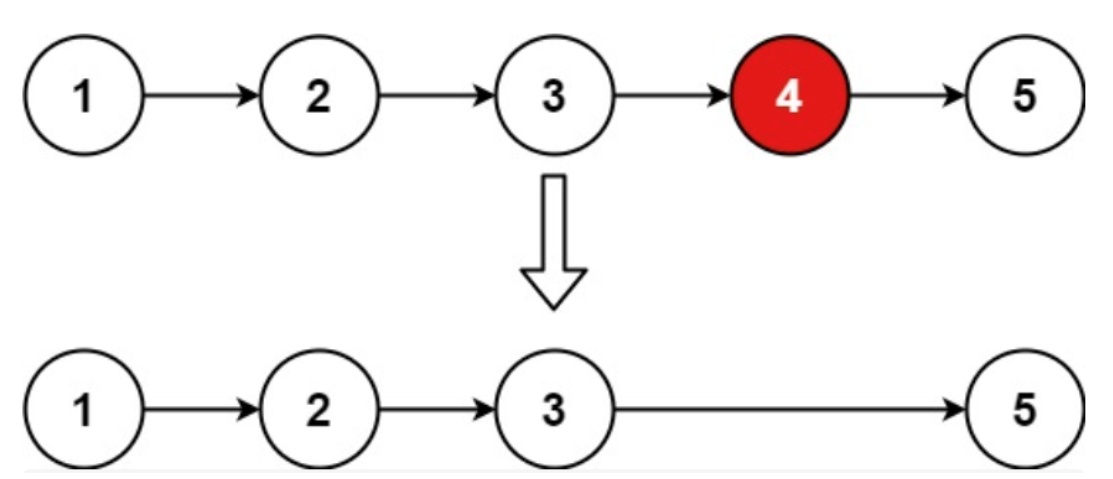
B 重新放置石块

有序集合模拟
class Solution {
public:
vector<int> relocateMarbles(vector<int> &nums, vector<int> &moveFrom, vector<int> &moveTo) {
set<int> s{nums.begin(), nums.end()};
for (int i = 0; i < moveFrom.size(); i++) {
s.erase(moveFrom[i]);
s.insert(moveTo[i]);
}
return vector<int>{s.begin(), s.end()};
}
};
C 将字符串分割为最少的美丽子字符串
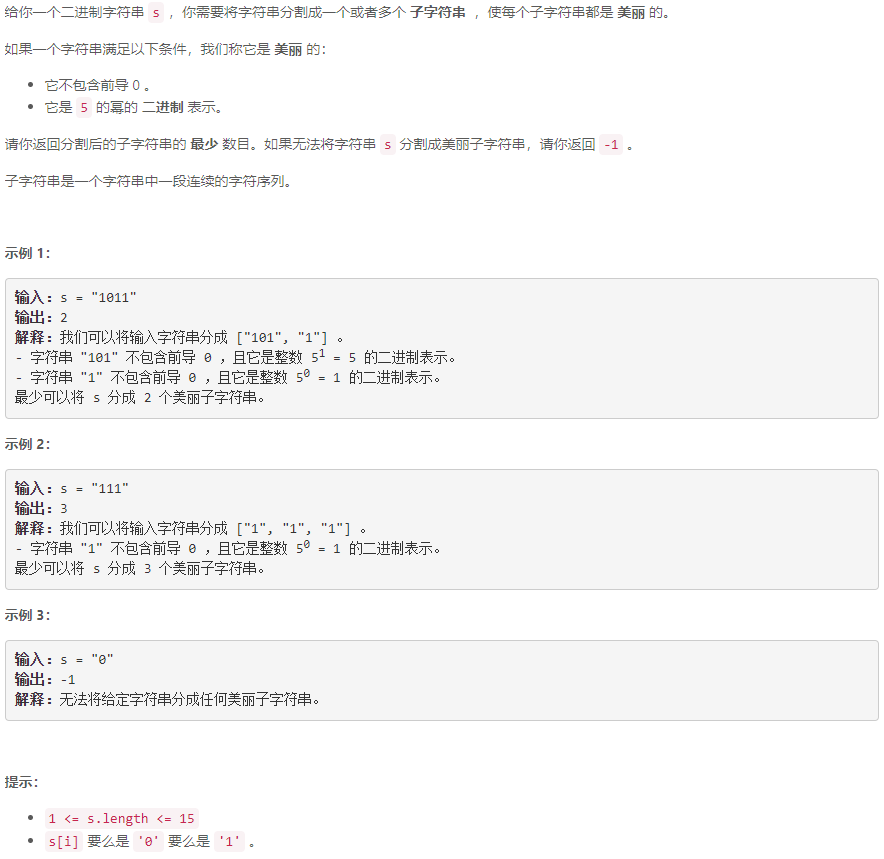
动态规划: 设 s s s长为 n n n, 定义 p l p_{l} pl为将 s [ l , n ) s[l,n) s[l,n)分割为最少的美丽子字符串的子串数, 若 s [ l , n ) s[l,n) s[l,n)对应的数为5的幂则 p l p_{l} pl=1, 否则有转移方程: p l = m i n { p r + 1 ∣ l < r < n 且 s [ l , r ) 对应的数是 5 的幂 } p_l= min\{p_{r}+1 \;|\; l<r<n \; 且 \; s[l,r)对应的数是5的幂 \} pl=min{pr+1∣l<r<n且s[l,r)对应的数是5的幂}
class Solution {
public:
int getval(string s) {//2进制串转10进制数
int cur = 0;
for (auto c: s)
cur = cur * 2 + c - '0';
return cur;
}
bool ispow5(int val) {//判断是否为5的非负整数幂
for (; val % 5 == 0; val /= 5);
return val == 1;
}
int minimumBeautifulSubstrings(string s) {
int n = s.size();
vector<int> p(n, INT32_MAX);//初始化状态为无效
if (s[n - 1] == '1')
p[n - 1] = 1;
for (int l = n - 2; l >= 0; l--)
if (s[l] != '0') {//不能有前导零
if (ispow5(getval(s.substr(l))))
p[l] = 1;
for (int r = l + 1; r < n; r++)
if (p[r] != INT32_MAX) {//p[r]状态有效
if (ispow5(getval(s.substr(l, r - l))))
p[l] = min(p[l], p[r] + 1);
}
}
return p[0] == INT32_MAX ? -1 : p[0];
}
};
D 黑格子的数目


哈希: 枚举coordinates中的黑色格子, 每个黑色格子最多能使周围的4个块的块内黑格子数加1, 用哈希记录出现过的块的块内黑格子数.
class Solution {
public:
vector<long long> countBlackBlocks(int m, int n, vector<vector<int>> &coordinates) {
map<pair<int, int>, int> cnt;//块左上角的坐标 -> 块内黑格子数
int dx[4] = {0, -1, -1, 0};
int dy[4] = {-1, -1, 0, 0};
for (auto &p: coordinates) {
for (int k = 0; k < 4; k++) {
int nx = p[0] + dx[k];
int ny = p[1] + dy[k];
if (nx < 0 || nx >= m - 1 || ny < 0 || ny >= n - 1)
continue;
cnt[{nx, ny}]++;//块左上角的坐标为(nx,ny)的块的块内黑格子数更新
}
}
vector<long long> res(5);
for (auto &[_, v]: cnt)
res[v]++;
res[0] = 1LL * (m - 1) * (n - 1) - accumulate(res.begin() + 1, res.end(), 0);
return res;
}
};





![LeetCode[470]用Rand7()实现Rand10()](https://img-blog.csdnimg.cn/1c92716a603b4b7ebfb1124e6709bf56.png)