在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例 1：

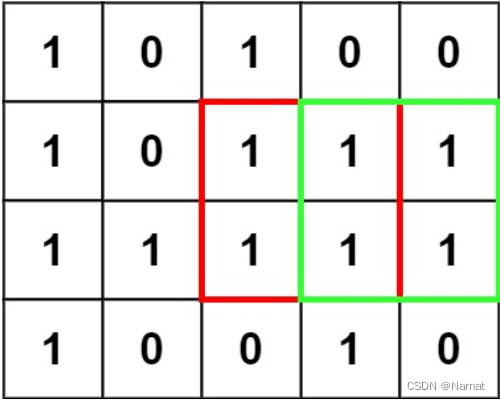
输入：matrix =
[[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：4

示例 2：

输入：matrix = [[“0”,“1”],[“1”,“0”]]
输出：1

示例 3：

输入：matrix = [[“0”]]
输出：0

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 ‘0’ 或 ‘1’

解题思路：

暴力破解：

1.注意题目中求的是最大正方形，不包括长方形

2.判断可能的最大正方形的边长

int mblen = Math.min(x - i, y - j);

3.判断正方形对角线是否为‘1’

for(int k = 1; k < mblen; k ++) {
                       
        			   if(matrix[i + k][j + k] == '0') { 
        				   check = false;
        				   break;//检查对角线
        			   }

4.若而对角线为‘1’判断正方形对角线两边是否都为‘1’

     			   for(int m = 0; m < k; m ++) {//检查正方形对角线两边是否都为1
        				  if(matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') { 
        					  check = false;
        					  break;
        				  }
        			   }

完整暴力破解代码：

class Solution {
    public int maximalSquare(char[][] matrix) {
           if(matrix.length == 0 || matrix[0].length == 0) return 0;
           int maxslen = 0;
           int x = matrix.length;
           int y = matrix[0].length;
           for(int i = 0; i < x; i ++)
        	   for(int j = 0; j < y; j ++) {
        		 if(matrix[i][j] == '1') {//在第一个为1的前提下才能检查后面的
                   maxslen = Math.max(1, maxslen);
        		   int mblen = Math.min(x - i, y - j);
        		   boolean check = true; 
        		   for(int k = 1; k < mblen; k ++) {
                       
        			   if(matrix[i + k][j + k] == '0') { 
        				   check = false;
        				   break;//检查对角线
        			   }
        			   
        			   for(int m = 0; m < k; m ++) {//检查正方形对角线两边是否都为1
        				  if(matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') { 
        					  check = false;
        					  break;
        				  }
        			   }
        			   
        			   if(check) maxslen = Math.max(maxslen, k + 1);//都为1更新//or check == true;
        			   else break;//否者没必要继续更新下去了
        		   }
        	   }
        	  }
           return maxslen * maxslen;
    }
}

---

动态规划：

1.设立dp[i][j] 即以（i， j）点为正方形右下角的最大边长

2.边界问题当 i=0 || j =0时dp[i][j] 最大为1

3.dp[i][j]由其左边、右边、左上角的最小值决定

4.

5.

6.

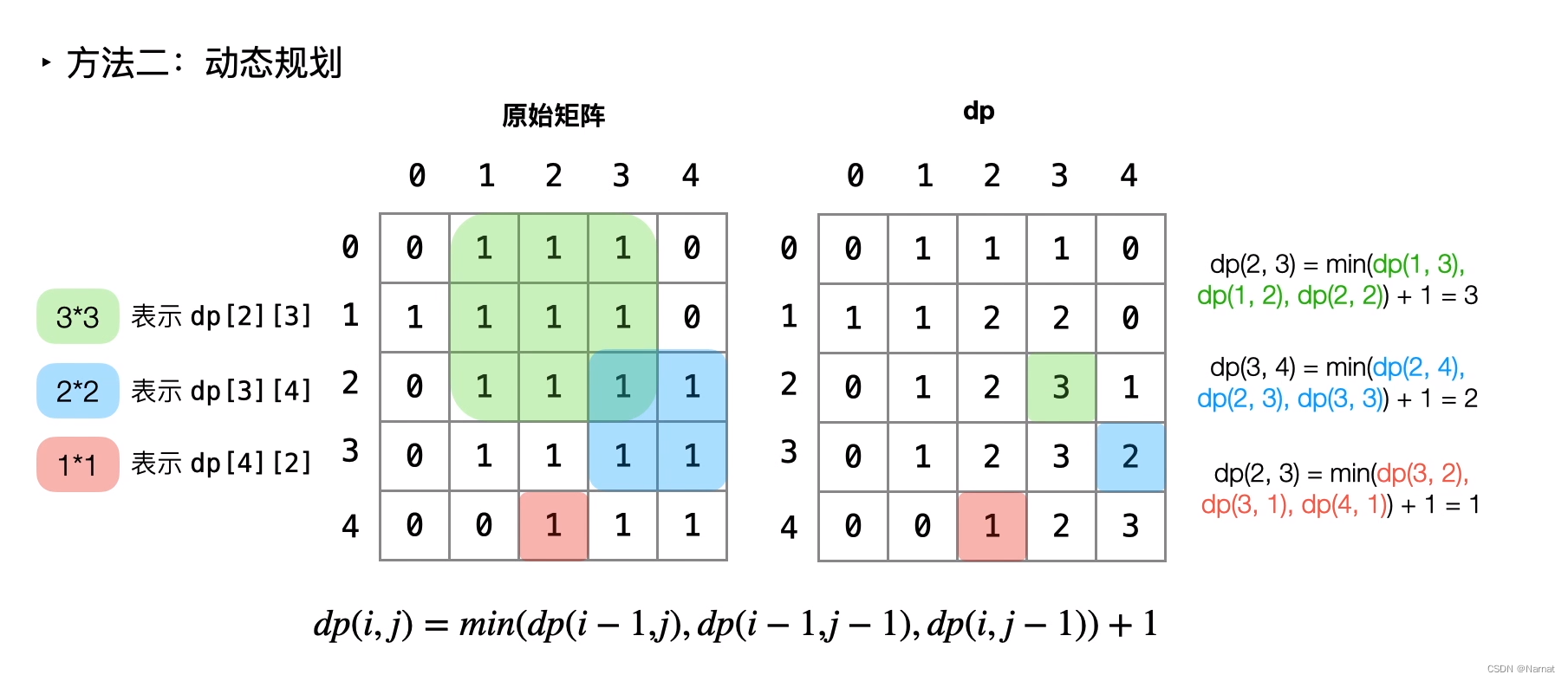
动态规划代码:

class Solution {
    public int maximalSquare(char[][] matrix) {
           int x = matrix.length;
           int y = matrix[0].length;
           if(x == 0 || y == 0) return 0;
           int dp[][] = new int[x][y];
           int maxlen = 0;
           for(int i = 0;i < x; i ++)
        	   for(int j = 0; j < y; j ++) {
        		   if(matrix[i][j] == '1') {
        			   if(i == 0 || j == 0) dp[i][j] = 1;
        			   else dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i - 1][j - 1], dp[i][j - 1])) + 1;
        		   }
        		   maxlen = Math.max(maxlen, dp[i][j]);
        	   }
           return maxlen * maxlen;
    }
}

动态规划优点在于用更多空间储存前面的计算的成果，使得在计算新的点时可以借助前面的成果迭代过来，类似于将四阶楼梯，分成一节一节去爬，前面一节会对后面一节产生辅助作用。