一.表是什么

【1】定义：表，又称为线性表。线性表L是n个相同类型数据元素a(1),a(2),...,a(n)组成的有限序列。
【2】相关概念：
表长：线性表中元素的个数，n=0时为空表。

【3】基本运算（共七种）：
ListEmpty(L):测试表L是否为空
ListLength(L):表L的长度
ListLocate(x,L):元素x在表L中的位置。若x在表中重复出现多次，则返回最前面的x的位置。
ListRetrieve(k,L):返回表L的位置k处的元素。表中没有位置k是，该运算无定义。
ListInsert(k,x,L):在表L的位置k之后插入元素x，并将原来占据该位置的元素及其后面的元素依次后移一个位置。若表中没有位置k，则该运算无定义。
ListDelete(k,L):从表L中删除位置k处的元素，并返回被删除的元素。如果表中没有位置k时，则该运算无定义。
PrintList(L):将表L中所有元素按位置的先后次序打印输出。

二.用动态数组实现表

1.顺序表概念
用一组地址连续的存储单元(数组)存放一个线性表叫顺序表
2.实现代码（就是在编写上述七种基本运算的函数的基础上，又因为是动态数组，需要增加初始化函数和释放空间的函数，所以这里实现了九种函数）【这里存储的元素取int】

#include<stdio.h>
#include<stdlib.h> 
//定义（因为还有表长，最大长度等属性，所以可用结构体或类来封装属性， 
//又因为我们是使用c语言，没有类，所以我们把表定义为结构体 
typedef struct alist *List;//表指针 
typedef struct alist{
	int n;//表长，当表为空时，n=0
	int maxsize;//表示线性表的最大长度
	int *table;//表元素数组,这里使用的是int型，当然也可以其他类型 
};  
//1.表结构初始化
//分配大小为size的空间给表数组table,并返回初始化为空的表。
List ListInit(int size){
	List L;
	L=(List)malloc(sizeof(alist));//作用？ 
	L->table=(int *)malloc(size*sizeof(int));
	L->maxsize=size;
	L->n=0;
	return L; 
} 
//2.判断表L是否为空
int ListEmpty(List L){
	if(L->n==0)
		return true;
	else
		return false; 
} 
//3.求表L的长度
int GetLength(List L){
	return L->n;
} 
//4.返回表L的位置k处的元素
int ListRetrieve(int k,List L){
	if(k<1||k>L->n)
		return -2147483648;//判断k值是否合理，若不合理，返回负数最小值 
	return L->table[k-1];
}
//5. 返回元素x在表中的第一个位置，当元素x不在表中时返回0
int ListLocate(int x,List L){
	for(int i=0;i<L->n;i++){
		if(L->table[i]==x)
			return i++;//真实位置比索引多1 
	}
	return 0;//元素不在表中返回0 
} 
//6.在表L的位置k之后插入元素x 
void ListInsert(int k,int x,List L){
	if(k<0||k>L->n)
		return;//判断k值是否合理，若不合理，返回
	for(int i=L->n-1;i>=k;i--)
		L->table[i+1]=L->table[i];
	L->table[k]=x;
	L->n++;
}
//7.从表L中删除位置k处的元素
int ListDelete(int k,List L){
	if(k<1||k>L->n)
		return -2147483648;
	int x=L->table[k-1];
	for(int i=k;i<L->n;i++)
		L->table[i-1]=L->table[i];
	L->n--;
	return x;
}
//8.按位置次序输出表L中元素
void PrintList(List L){
	for(int i=0;i<L->n;i++)
		printf("%d ",L->table[i]);
	printf("\n");
} 
//9.释放动态分配的数组空间
void ListFree(List L){
	free(L->table);
	free(L);
} 

三.用链表(指针)实现表

1.链表概念
用一组任意的存储单元存储线性表的数据元素，利用指针将其串联在一起，实现了用不相邻的存储单元存放逻辑上相邻的元素。以这种链式存储结构存储的表称为链表。
2.用动态数组实现表的优缺点（比较）：
优点：存储空间紧凑；逻辑相邻，物理相邻，无须为表示表中元素之间的顺序关系增加额外的存储空间；可随机存取任一元素，查找速度快
缺点：插入和删除耗时；表容量难以扩充
3.实现代码【这里存储的元素取int】

#include<stdio.h>
#include<stdlib.h>
//定义 
typedef struct node* link;//表结点指针类型 
typedef struct node{//表结点类型 
	int element;//表元素 
	link next;//指向下一写点的指针 
}Node;
typedef struct llist *List;//单链表指针类型
typedef struct llist{//单链表类型
	//链表表首指针，当前结点指针，链表表尾指针 
	link first,curr,last; 
}Llist; 
//1.产生一个新结点 
link NewNode(){
	return (link)malloc(sizeof(Node));
}
//2.表结构初始化
分配大小为size的空间给表数组table,并返回初始化为空的表。 
List ListInit(){
	List L=(List)malloc(sizeof *L);
	L->first=0;
	return L;
} 
//3.判断表L是否为空
//只要看表首指针first是否为空指针 
int ListEmpty(List L){
	return L->first==0;
}
//3.求表L的长度
int ListLength(List L){
	int len=0;
	link p=L->first;
	//通过对表L进行线性扫描计算 
	while(p){
		len++;
		p=p->next;
	}
	return len;
}
//4.返回表L的位置k处的元素  
int ListRetrieve(int k,List L){
	if(k<1)
		exit(1);//不正常退出 
	link p=L->first;
	int i=1;
	while(i<k&&p){
		p=p->next;
		i++;
	}
	return p->element; 
} 
//5. 返回元素x在表中的第一个位置，当元素x不在表中时返回0
int ListLocate(int x,List L){
	int i=1;
	link p=L->first;
	while(p&&p->element!=x){
		p=p->next;
		i++;
	} 
	return p?i:0;
}
//6.在表L的位置k之后插入元素x 
void ListInsert(int k,int x,List L){
	if(k<0)
		exit(1);
	link p=L->first;
	for(int i=1;i<k&&p;i++)
		p=p->next;
	link y=NewNode();
	y->element=x;
	if(k){
		y->next=p->next;
		p->next=y;
	}else{
		y->next=L->first;
		L->first=y;
	}
}
//7.从表L中删除位置k处的元素
int ListDelete(int k,List L){
	if(k<1||!L->first)
		exit(1);
	link p=L->first;
	if(k==1)
		L->first=p->next;
	else{
		link q=L->first;
		for(int i=1;i<k-1&&q;i++)
			q=q->next;
		p=q->next;
		q->next=p->next;
	}
	int x=p->element;
	free(p);
	return x;
}
//8.按位置次序输出表L中元素
void PrintList(List L){
	for(link p=L->first;p;p=p->next)
		printf("%d",p->element);
} 

四.用间接寻址方法实现表

1.实现：让动态数组中原来存储元素的地方改为存储指向元素的指针​​​​​。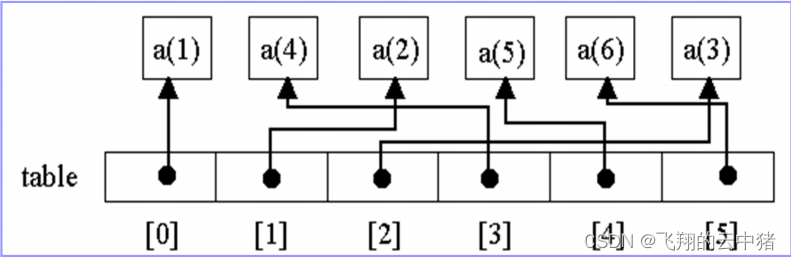

2.优点：就是在动态数组实现表的基础上进行优化。
这时候你会疑问这只是让动态数组中原来存储元素的地方改为存储指向元素的指针，然而进行各种增删改查的算法仍然与动态数组一模一样​​​​​，只是你要操作元素还需要通过先获取指针再来操作元素，这样的话从直接操作元素变为间接操作，为什么会更好？
这是因为在实现在位置k后插入元素和删除位置为k的元素这两个方法的时候，不实际移动元素而只移动指向元素的指针。虽然算法所需的计算时间O(n)仍然相同，但在每个元素占用的空间较大时，该算法比数组实现的表的插入算法快得多。
简单说就是移动指针的速度比直接移动元素的速度快。元操作的速度快。
3.实现代码【这里存储的元素取int】

#include<stdio.h>
#include<stdlib.h>
//定义
typedef int *addr;//这里表元素的类型假设为int
typedef struct indlist *List;
typedef struct indlist {
	int n;//表长
	int curr;//当前位置
	int maxsize;//数组上界
	addr *table;//存储表元素指针的数组
} Indlist;
addr NewNode() {
	return (addr)malloc(sizeof(addr));
}
//1.表结构初始化
//分配大小为size的空间给表数组table,并返回初始化为空的表。
List ListInit(int size) {
	List L=(List)malloc(sizeof *L);
	L->n=0;
	L->maxsize=size;
	L->table=(addr*)malloc(size*sizeof(addr));
	return L;
}
//2.判断表L是否为空
int ListEmpty(List L) {
	return L->n==0;
}
//3.求表L的长度
int ListLength(List L) {
	return L->n;
}
//4.返回表L的位置k处的元素
int ListRetrieve(int k,List L) {
	if(k<1||k>L->n)
		exit(1);
	return *L->table[k-1];
}
//5. 返回元素x在表中的第一个位置，当元素x不在表中时返回0
int ListLocate(int x,List L) {
	for(int i=0; i<L->n; i++) {
		if(*L->table[i]==x)
			return ++i;
	}
	return 0;
}
//6.在表L的位置k之后插入元素x 
void ListInsert(int  k,int x,List L) {
	if(k<0||k>L->n)
		exit(1);
	if(L->n==L->maxsize)
		exit(1);
	for(int i=L->n-1; i>=k; i--)
		L->table[i+1]=L->table[i];
	L->table[k]=NewNode();
	*L->table[k]=x;
	L->n++;
}
//7.从表L中删除位置k处的元素
int ListDelete(int k,List L) {
	int x;
	addr p;
	if (k<1 || k>L->n) 
		exit(1);
	p = L->table[k-1];
	x=*p;
	for (int i=k; i<L->n; i++) 
		L->table[i-1]=L->table[i];
	L->n--;
	free(p);
	return x;
}
//8.按位置次序输出表L中元素
void PrintList(List L){
	for(int i=0;i<L->n;i++)
		printf("%d ",*L->table[i]);
	printf("\n");
}

五.用游标实现表

比较少用，先跳过，以后有时间再添加。