检验样本正态性

简介

在统计学中很多推论与正态分布有关，并且很多统计量构造为满足正态分布的形式，很多分布在特定条件近似于正态分布。因此，在统计推断中经常需要判断样本的正态性。本文介绍一些常用的方法。

环境和数据准备：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
from statsmodels.stats import diagnostic

# check out https://github.com/Paradiseeee/Heaven
from Heaven import mpl_tools
mpl_tools.Begin().setting()

# 正态分布样本与二项分布样本（两者方差均值一致）
n_sample = stats.norm.rvs(2, np.sqrt(1.6), 100)
b_sample = stats.binom.rvs(10, 0.2, size=100)

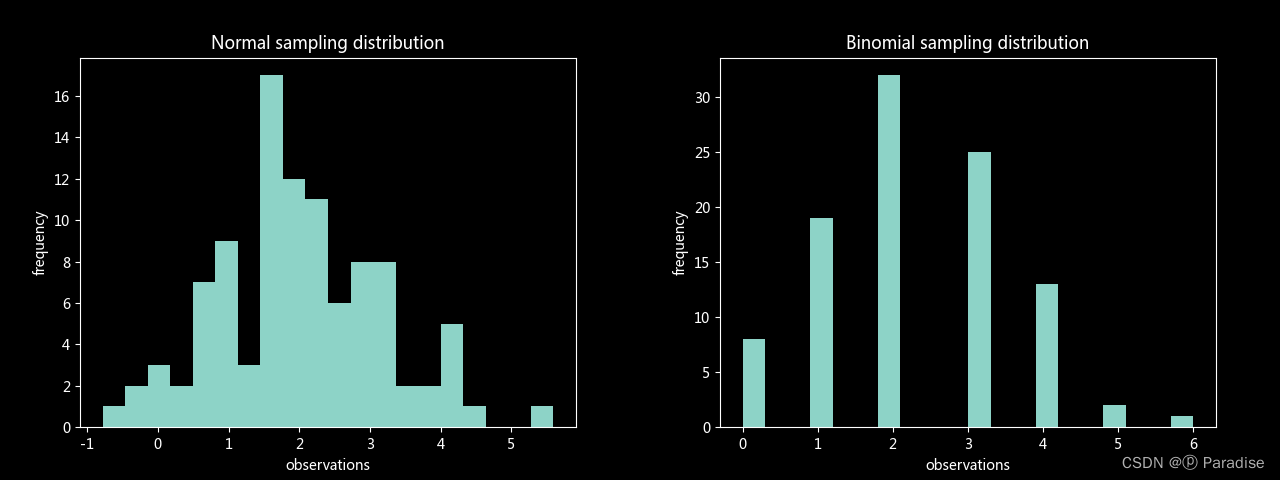
plt.hist(n_sample, bins=20)
plt.title('Normal sampling distribution')
plt.xlabel('observations'); plt.ylabel('frequency'); plt.show()

plt.hist(b_sample, bins=20)
plt.title('Binomial sampling distribution')
plt.xlabel('observations'); plt.ylabel('frequency'); plt.show()

请添加图片描述

一、通过绘图直观判断

频数（分布密度）图：

通过图像对比判断样本是否服从理论总体的分布，需要总体分布已知（或假设拟合相应分布）

# 模拟总体
pop = stats.norm.rvs(2, np.sqrt(1.6), 10000)

# 绘制常见的分布图形
def plot_dist(rv, title):
    axes = mpl_tools.Func().get_subplots('AABC')
    # 频数密度图
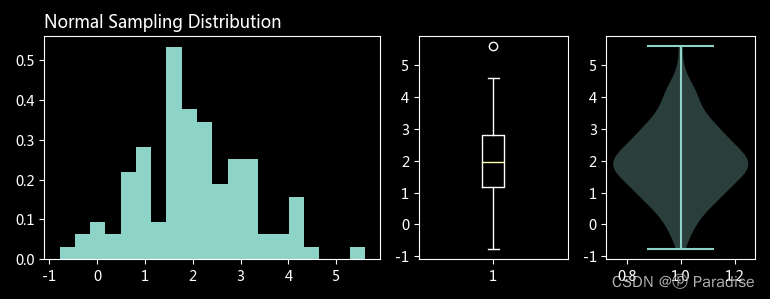
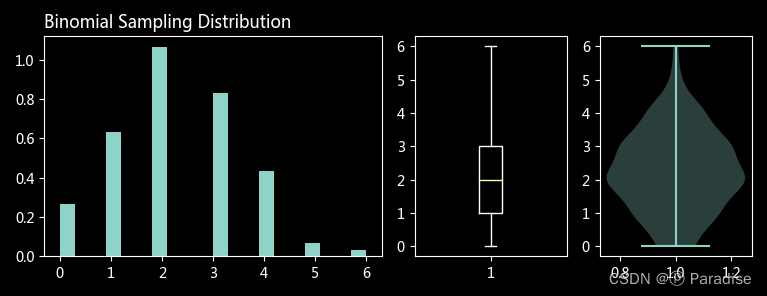
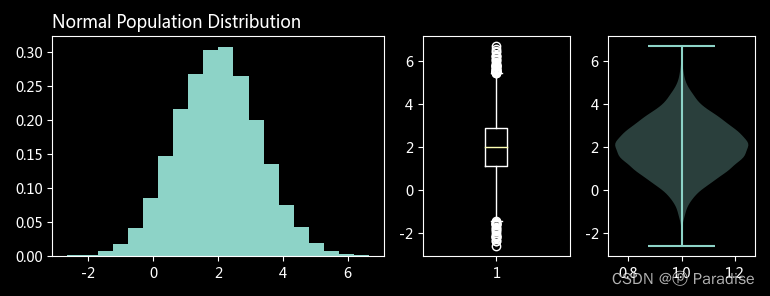
    axes['A'].hist(rv, bins=20, density=True)
    # 箱形图
    axes['B'].boxplot(rv)
    # 小提琴图（竖起来的 KDE 图）
    axes['C'].violinplot(rv)
    plt.title(title, loc='left')
    plt.show()

plot_dist(n_sample, 'Normal Sampling Distribution')
plot_dist(b_sample, 'Binomial Sampling Distribution')
plot_dist(pop, 'Normal Population Distribution')

请添加图片描述

Q-Q 图

通过抽样和总体的分位数进行对比

# stats.probplot 严格来说是“概率图”，坐标轴未缩放的 Q-Q 图
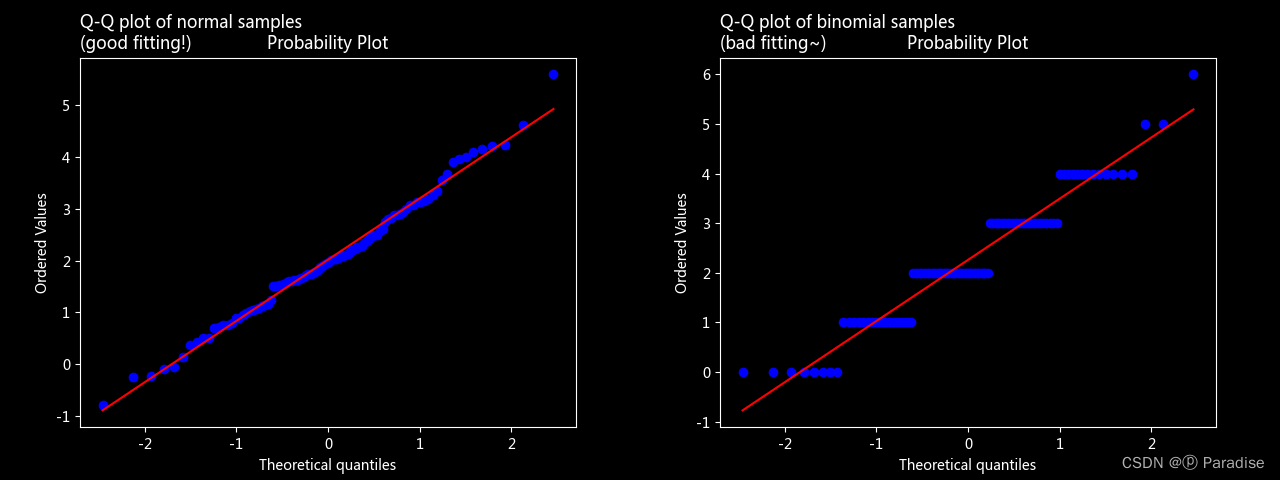
stats.probplot(n_sample, dist='norm', plot=plt)
plt.title('Q-Q plot of normal samples \n(good fitting!)', loc='left')
plt.show()

stats.probplot(b_sample, dist='norm', plot=plt)
plt.title('Q-Q plot of binomial samples \n(bad fitting~)', loc='left')
plt.show()

请添加图片描述

二、通过参数量化比较

绘图方法优点在于直观，但是得出结论只能是粗略的，只是“看起来像”，缺乏可信度。通过统计参数对比可以更准确的量化样本的正态性。

Shapiro-Wilk test

results = pd.DataFrame(
    {'normal':[None]*4, 'binomial':[None]*4}, 
    index=['Shapiro', 'KS', 'Anderson', 'Lilliefors']
)

# 构造了一个统计量，该统计量越高，表示样本越有可能是正态分布
ntest = stats.shapiro(n_sample)
btest = stats.shapiro(b_sample)
results.loc['Shapiro', 'normal'] = (ntest.statistic, ntest.pvalue)
results.loc['Shapiro', 'binomial'] = (btest.statistic, btest.pvalue)

Kolmogorov-Smirnov test

ntest = stats.kstest(n_sample, stats.norm.cdf, args=(2, np.sqrt(1.6)))
btest = stats.kstest(b_sample, stats.norm.cdf, args=(2, np.sqrt(1.6)))
results.loc['KS', 'normal'] = (ntest.statistic, ntest.pvalue)
results.loc['KS', 'binomial'] = (btest.statistic, btest.pvalue)

Anderson-Darling test

ntest = stats.anderson(n_sample, dist='norm')
btest = stats.anderson(b_sample, dist='norm')
# 不提供连续的 p 值，取显著性水平为 1% 时的临界值
results.loc['Anderson', 'normal'] = (ntest.statistic, ntest.critical_values[ntest.significance_level == 1][0])
results.loc['Anderson', 'binomial'] = (btest.statistic, btest.critical_values[ntest.significance_level == 1][0])

Lilliefors’ test

ntest = diagnostic.lilliefors(n_sample, dist='norm')
btest = diagnostic.lilliefors(b_sample, dist='norm')
results.loc['Lilliefors', 'normal'] = ntest
results.loc['Lilliefors', 'binomial'] = btest

results = results.applymap(lambda x: tuple([round(i, 5) for i in x]))
print(results.to_markdown())

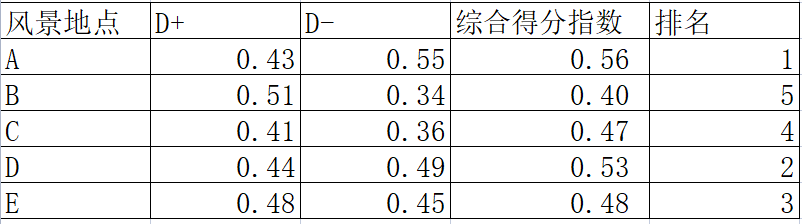
	normal	binomial
Shapiro	(0.99032, 0.6905)	(0.93856, 0.00016)
KS	(0.07716, 0.56435)	(0.23, 4e-05)
Anderson	(0.3403, 1.053)	(2.65129, 1.053)
Lilliefors	(0.06062, 0.48814)	(0.17224, 0.001)

所有结果如上表，其中每个元组的第一位是对应的统计量，第二位是 p 值或者临界值，具体解释如下：

对于 Shapiro 测试，统计量越大越接近正态分布（用于支撑原假设），p 值越小越拒绝原假设。从统计量来看，两个分布的样本都接近于正态分布，但是二项分布样本的 p 值明显小，在一般的显著性水平下（5%）可以拒绝原假设，即不服从正态分布。
对于 KS 测试，正态样本的 p 值大于显著性水平，二项分布样本的 p 值小于显著性水平，拒绝原假设。
对于 Anderson 测试，第一项是统计量，第二项是对应显著性水平为 1% 时的临界值（对于正态测试可选的有 15%、10%、5%、2.5%、1%，对于其他分布测试有不同的序列）。可以看到对于正态样本，统计量小于临界值，在 1% 的显著性水平下不能拒绝原假设；对于二项分布样本，拒绝原假设，样本不服从正态分布（2.65 > 1.05）。
对于 Lilliefors 测试，根据第二项的 p 值进行判断，可以看到二项分布样本的 p 值为 0.001，可以拒绝原假设，不服从正态分布。