给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形，请你计算并返回两个矩形覆盖的总面积。

每个矩形由其 左下 顶点和 右上 顶点坐标表示：

第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。 第二个矩形由其左下顶点 (bx1, by1)
和右上顶点 (bx2, by2) 定义。

示例 1：

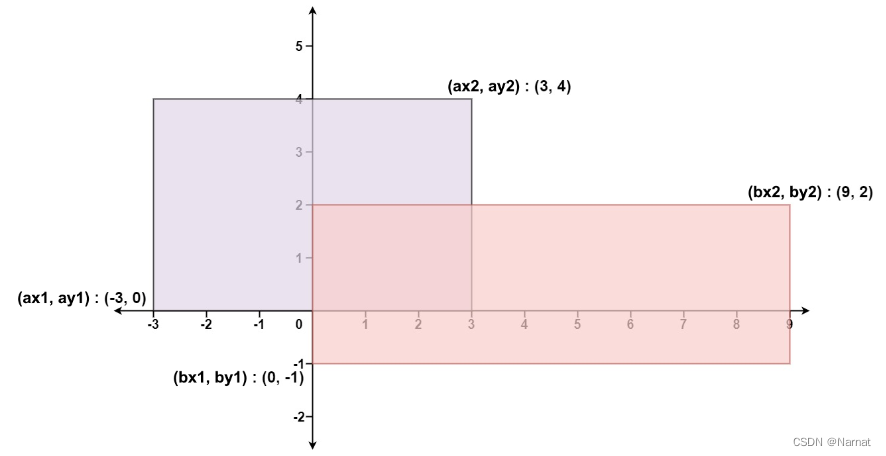
输入：ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出：45

示例 2：

输入：ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
输出：16

提示：

-10^4 <= ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 <= 10^4

解题思路：

1.两个矩形的关系无非分为相交与不相交两种

2.如果有重合部分，那么重合部分必然也是矩形

3.计算两个矩形面积 - 重合部分面积

由上图可知:
重合部分矩形的左下角横坐标 = max(ax1, bx1),纵坐标 = max(ay1, by1)
重合部分矩形的右下角横坐标 = min(ax2, bx2),纵坐标 = min(ay2, by2)

4.最后计算重合部分面积是否大于0

代码：

class Solution {
    public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
           int area = 0;
           int area1 = (ax2 - ax1) * (ay2 - ay1);  
           int area2 = (bx2 - bx1) * (by2 - by1);
           int xx1 = Math.max(ax1, bx1);
           int yy1 = Math.max(ay1, by1);
           int xx2 = Math.min(ax2, bx2);
           int yy2 = Math.min(ay2, by2);
           int area3 = Math.max(xx2 - xx1, 0) * Math.max(yy2 - yy1, 0);
           return area1 + area2 - area3;
    }
}