1 INTRODUCTION
- 由于6G的复杂管理机制,可以在基站收集历史数据——为克服训练数据集容量的限制提供了极大的便利
问题与挑战:
- 尽管元学习可以提高网络边缘智能(network edge intelligence)的性能,但其在无线网络(wireless networks)中的应用仍然面临一些独特的技术问题:
- 虽然可以在基站处生成多个元学习模型,但需要复杂的模型选择方案(model selection schemes),以适应不同的小样本学习任务
- 元学习模型是通过使用额外的无线电资源传输给用户的,这给无线网络带来了沉重的负担
文章贡献:
-
提出了一种基于元学习模型的无线网络小样本学习方案
- 通过使用历史数据在基站生成多个元学习模型,以适应用户的小样本学习任务
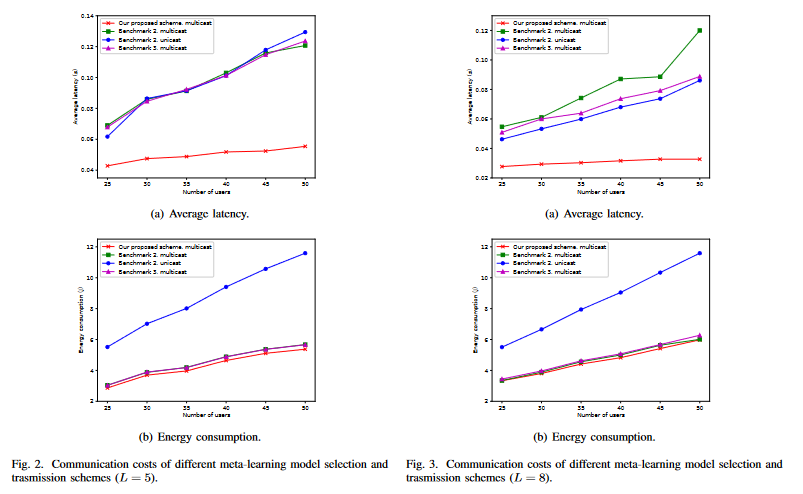
- 任务可以通过多播(multicasting)发送给用户,以提高频谱效率(spectrum efficiency)
-
设计了一种基于hedonic coalition formation的元学习模型选择算法
- 用来平均小样本学习模型的性能和元学习模型传输的通信成本之间的权衡
-
提供了仿真结果:方案可以在低通信成本的情况下显著提高小样本学习任务的性能
2 SYSTEM MODEL
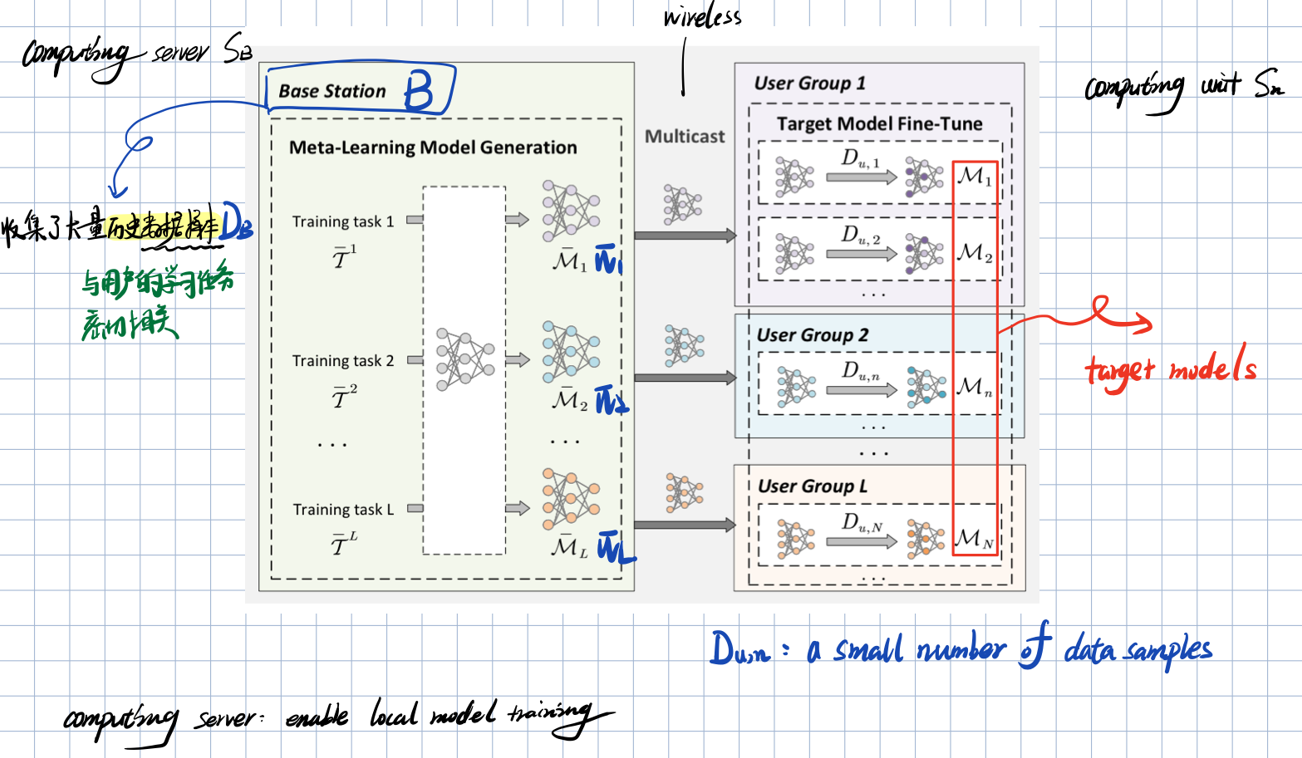
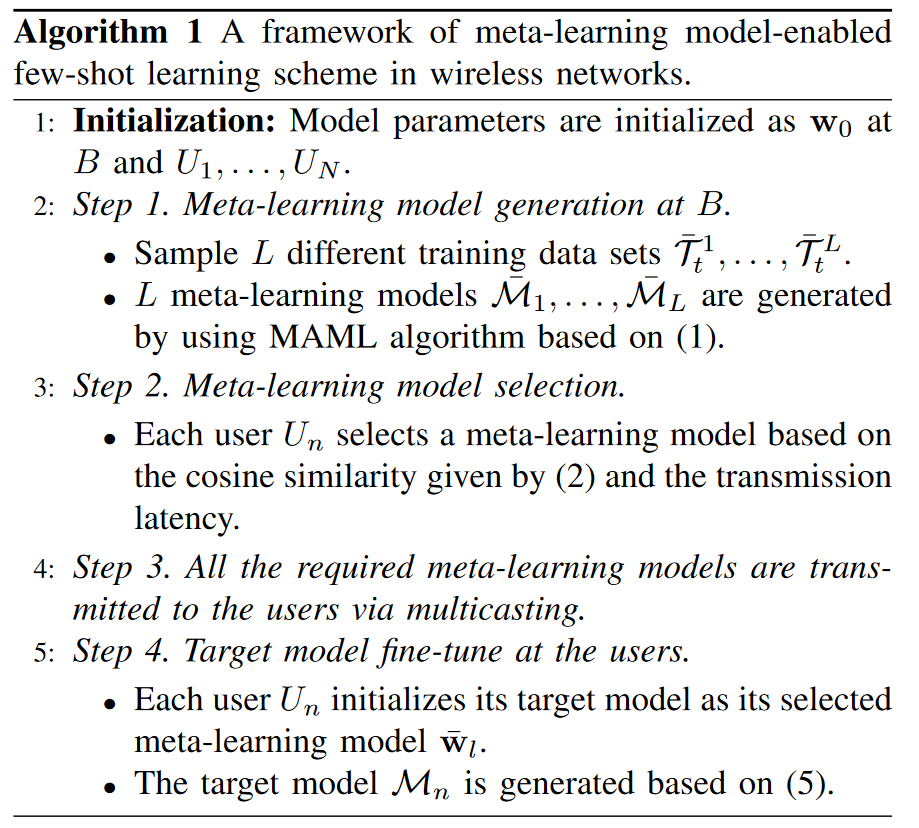
2.1 基站元学习模型生成
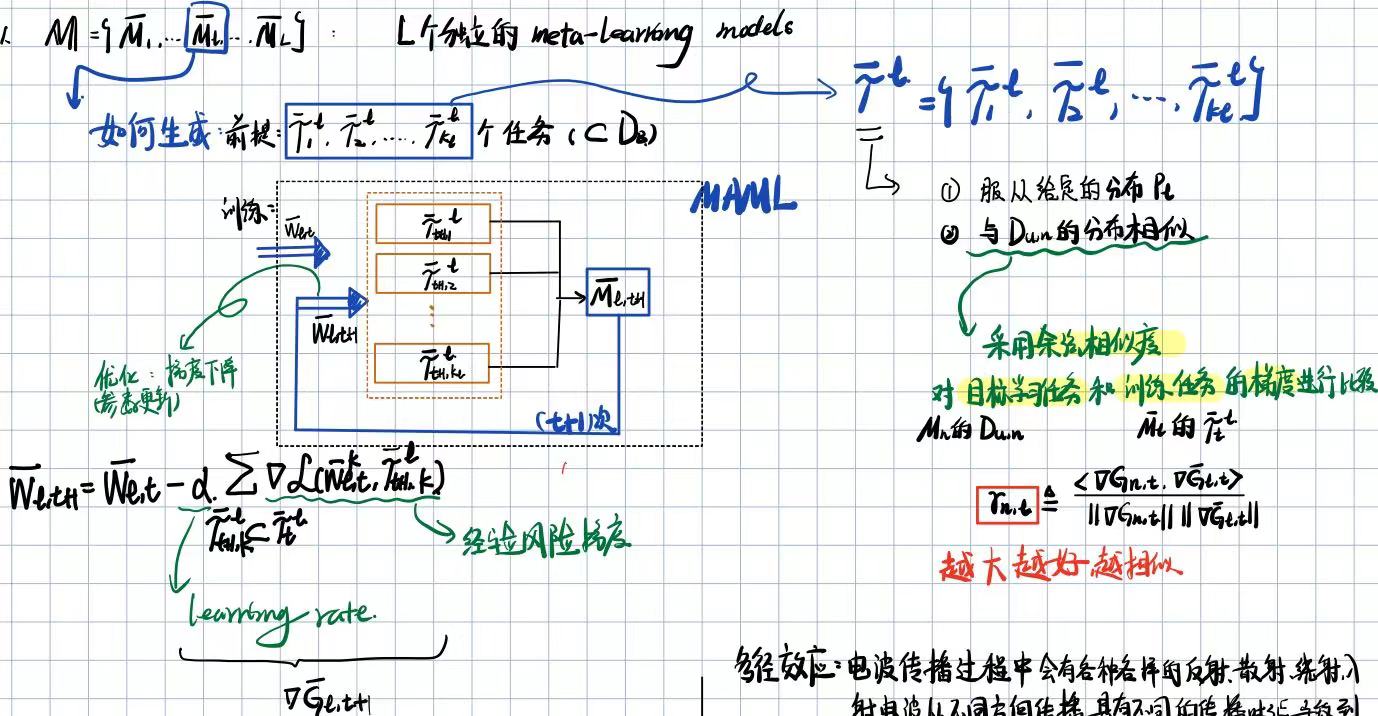
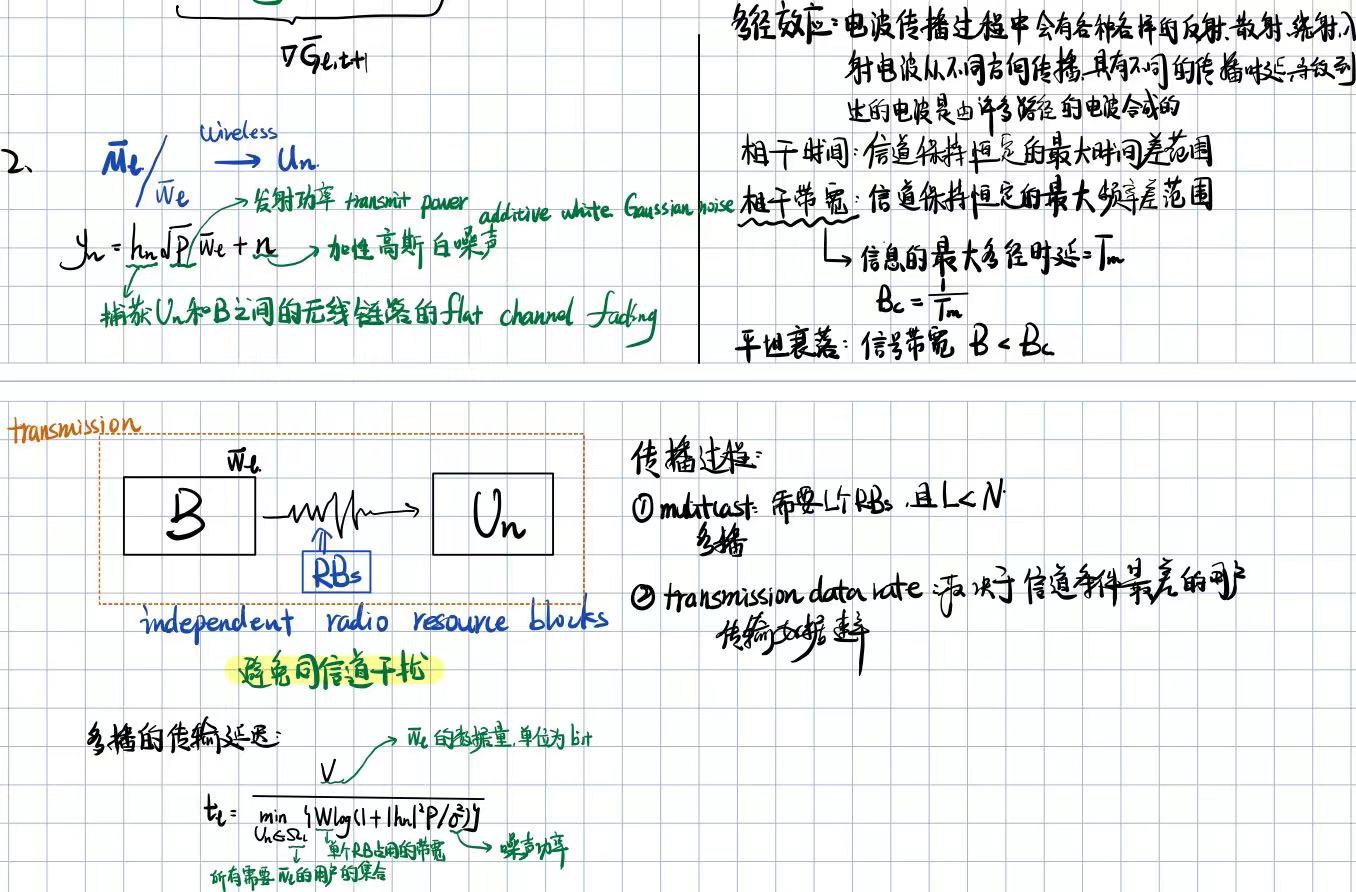
2.2 元学习模型参数传输
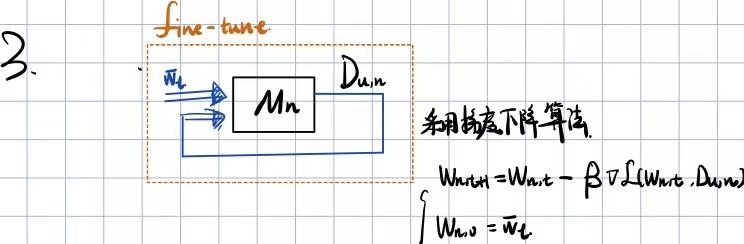
2.3 用户目标任务生成
3 A COALITION FORMATION GAME-BASED META-LEARNING MODEL SELECTION ALGORITHM
- 用户的元学习模型选择可以被建模为零一整数规划问题 zero-one integer programming problem
- 优化目标:通过最大化余弦相似性减去传输延迟来平衡小样本学习的性能和通信效率
挑战: 元学习模型参数的传播时延公式分母是最小值公式,从而采用导数方式进行优化时会很困难
作者想法: 模型选择问题可以表述为联盟形成博弈 coalition formation game —— a hedonic coalition formation-based meta-learning model selection algorithm
- coalition formation game: 玩家决定加入或离开联盟的原则是在不侵犯他人的情况下提高联盟的效用——效用函数应经过精心设计
3.1 Utility Function Formulation
每个用户加入联盟的效用被定义为用户减去联盟中的成本所获得的收益
考虑
U
n
U_n
Un 加入 联盟
R
l
R_l
Rl的效用函数:
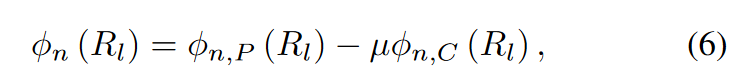
-
ϕ n , P \phi_{n,P} ϕn,P:用户加入联盟的报酬——payoff function:评估其目标模型的性能,可以设计为目标学习任务与其联盟相关元学习模型的训练任务之间的余弦相似性
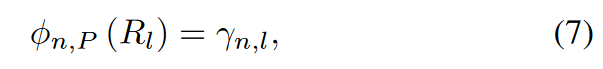
-
ϕ n , C \phi_{n,C} ϕn,C: 用户加如联盟的成本——cost function:为了减少元学习模型传输的通信开销,可以将成本函数设计为多播元学习模型的传输延迟

-
μ \mu μ:一个权重参数来控制收益和成本的影响
3.2 A Hedonic Coalition Formation-Based Meta-Learning Model Selection Algorithm
偏好关系 preference relation :一个玩家比另一个玩家更喜欢加入一个特定的联盟
论文建模:
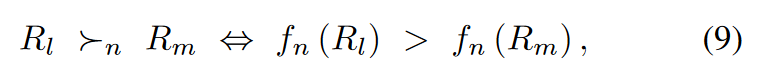
-
f
n
f_n
fn : 偏好函数
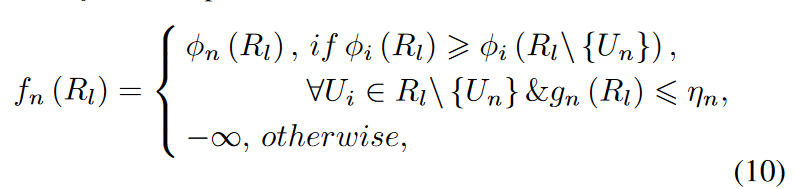
- g n ( R l ) g_n(R_l) gn(Rl): U n U_n Un访问然后离开联盟 R l R_l Rl的次数
- η n \eta_n ηn:允许访问然后离开某个联盟的最大次数
switch rule:


3.3 The Stability Analysis of Algorithm 2
论文提出的模型选择算法被证明总是可以收敛到一个Nash-Stable 划分结果
Nash-stable partition的定义:
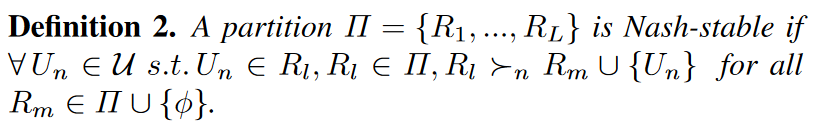
证明: 如果可以满足以下两个条件,则可以保证算法2的收敛性:
- 给定一个随机的初始联盟分布,再经过有限次选择 switch 操作可以收敛到一个最终的分区结果 Π f \Pi_f Πf
- 最终的分区结果是 Nash-stable
条件1具体说明:
- 在论文所提出的联盟形成博弈中的联盟数量是固定的,从而可能的分区次数是固定的 the number of possible partitions is finite
- 一个用户 U n U_n Un可以重新访问某个联盟的最大次数是 η n \eta_n ηn,达到这个次数后就可以访问新的联盟
可推出的结论:
- 所提出的基于特征联盟形成的算法是一系列切换操作 a sequence of switch operations
- 在某个时间点,每个切换操作将转向新访问的分区
- 由于分区的数量有限,切换操作序列总是收敛于一个最终分区 Π f \Pi_f Πf
条件2具体说明:
通过矛盾证明

4 SIMULATION RESULTS
数据集: Omniglot data set
模型: 卷积神经网络——网络由4个卷积层和1个全连接层组成——元学习模型和目标任务都采用
总带宽 total bandwidth: 50MHz
发射功率 transmit power: P = 40 dBm
噪声功率 noise power:
σ
2
\sigma^2
σ2 = -5 dBm
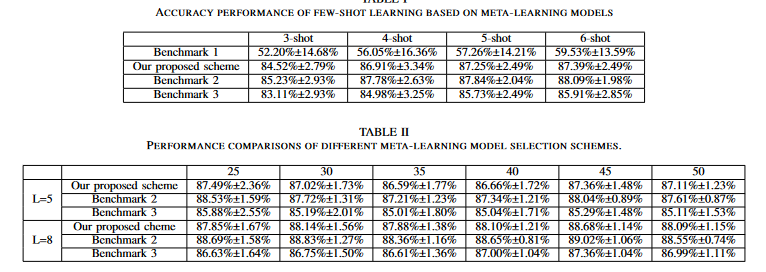
基准选择:
- 基准1:没有元学习模型——在没有元学习的情况下,直接基于少镜头学习任务对目标模型进行微调
- 基准2:基于余弦相似性的元学习模型选择——目标模型是基于元学习模型生成的,该模型是基于余弦相似性选择的
- 基准3:随机元学习模型选择——目标模型是基于随机选择的元学习模型生成的