全文下载链接:http://tecdat.cn/?p=20631
我们已经学习了如何处理混合效应模型。本文的重点是如何建立和_可视化_ 混合效应模型的结果(点击文末“阅读原文”获取完整代码数据)。
相关视频
设置
本文使用数据集,用于探索草食动物种群对珊瑚覆盖的影响。
knitr::opts_chunk$set(echo = TRUE)
library(tidyverse) # 数据处理
library(lme4) # lmer glmer 模型
me_data <- read_csv("mixede.csv")创建一个基本的混合效应模型:
该模型以珊瑚覆盖层为因变量(elkhorn_LAI),草食动物种群和深度为固定效应(c。urchinden,c.fishmass,c.maxD)和调查地点作为随机效应(地点)。
。
注意:由于食草动物种群的测量规模存在差异,因此我们使用标准化的值,否则模型将无法收敛。我们还使用了因变量的对数。我正在根据这项特定研究对数据进行分组。
summary(mod)## Linear mixed model fit by maximum likelihood ['lmerMod']
##
## AIC BIC logLik deviance df.resid
## 116.3 125.1 -52.1 104.3 26
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -1.7501 -0.6725 -0.1219 0.6223 1.7882
##
## Random effects:
## Groups Name Variance Std.Dev.
## site (Intercept) 0.000 0.000
## Residual 1.522 1.234
## Number of obs: 32, groups: site, 9
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 10.1272 0.2670 37.929
## c.urchinden 0.5414 0.2303 2.351
## c.fishmass 0.4624 0.4090 1.130
## c.axD 0.3989 0.4286 0.931
##
## Correlation of Fixed Effects:
## (Intr) c.rchn c.fshm
## c.urchinden 0.036
## c.fishmass -0.193 0.020
## c.maxD 0.511 0.491 -0.431
## convergence code: 0
## boundary (singular) fit: see ?isSingular绘制效应大小图:
如果您有很多固定效应,这很有用。
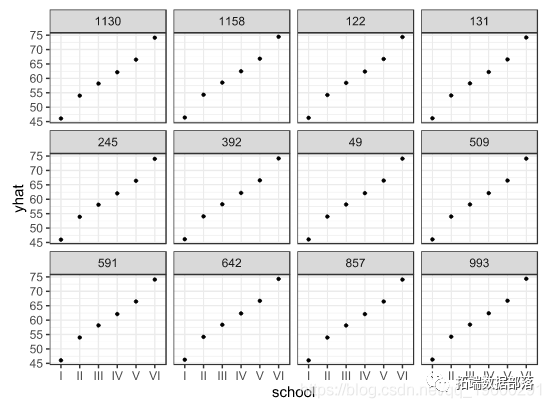
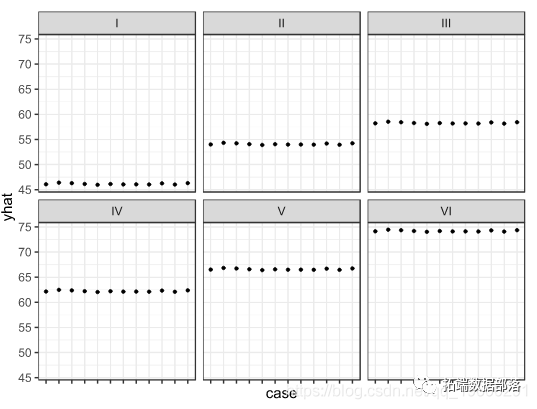
plot(mod)
点击标题查阅往期内容


左右滑动查看更多

01
02

03
04
效应大小的格式化图:
让我们更改轴标签和标题。
# 注意:轴标签应按从下到上的顺序排列。
# 要查看效应大小和p值,设置show.values和show.p= TRUE。只有当效应大小的值过大时,才会显示P值。
title="草食动物对珊瑚覆盖的影响")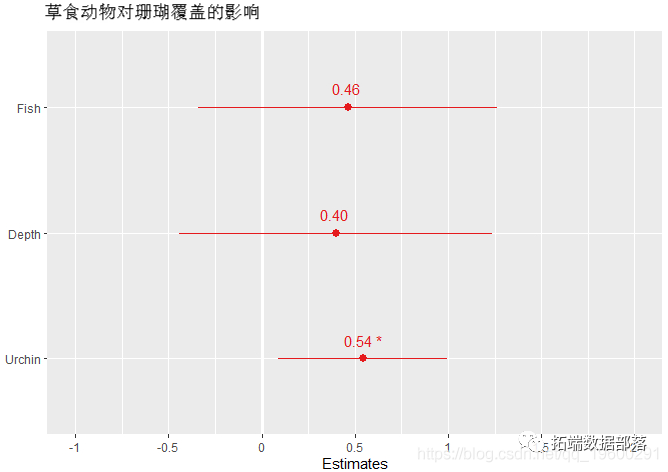
模型结果表输出:
创建模型摘要输出表。这将提供预测变量,包括其估计值,置信区间,估计值的p值以及随机效应信息。
tab(mod)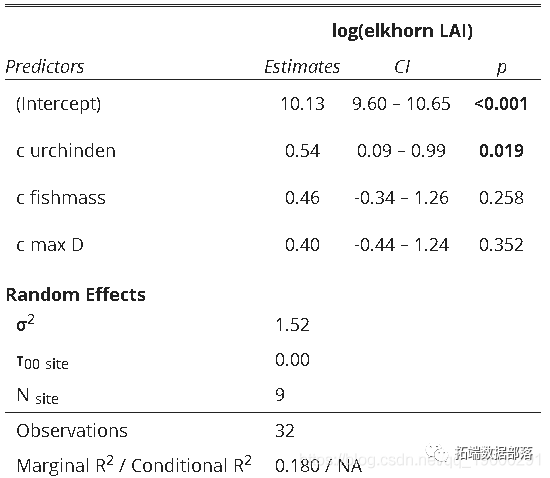
格式化表格
# 注:预测标签(pred.labs)应从上到下排列;dv.labs位于表格顶部的因变量的名称。
pred.labels =c("(Intercept)", "Urchins", "Fish", "Depth"),用数据绘制模型估计
我们可以在实际数据上绘制模型估计值!我们一次只针对一个变量执行此操作。注意:数据已标准化以便在模型中使用,因此我们绘制的是标准化数据值,而不是原始数据
步骤1:将效应大小估算值保存到data.frame中
# 使用函数。term=固定效应,mod=你的模型。
effect(term= "c.urchinden", mod= mod)
summary(effects) #值的输出##
## c.urchinden effect
## c.urchinden
## -0.7 0.4 2 3 4
## 9.53159 10.12715 10.99342 11.53484 12.07626
##
## Lower 95 Percent Confidence Limits
## c.urchinden
## -0.7 0.4 2 3 4
## 8.857169 9.680160 10.104459 10.216537 10.306881
##
## Upper 95 Percent Confidence Limits
## c.urchinden
## -0.7 0.4 2 3 4
## 10.20601 10.57414 11.88238 12.85314 13.84563# 将效应值另存为df:
x <- as.data.frame(effects)步骤2:使用效应值df绘制估算值
如果要保存基本图(仅固定效应和因变量数据),可以将其分解为单独的步骤。注意:对于该图,我正在基于此特定研究对数据进行分组。
#基本步骤:
#1创建空图
#2 从数据中添加geom_points()
#3 为模型估计添加geom_point。我们改变颜色,使它们与数据区分开来
#4 为MODEL的估计值添加geom_line。改变颜色以配合估计点。
#5 添加具有模型估计置信区间的geom_ribbon
#6 根据需要编辑标签!
#1
chin_plot <- ggplot() +
#2
geom_point(data , +
#3
geom_point(data=x_, aes(x= chinde, y=fit), color="blue") +
#4
geom_line(data=x, aes(x= chinde, y=fit), color="blue") +
#5
geom_ribbon(data= x , aes(x=c.urchinden, ymin=lower, ymax=upper), alpha= 0.3, fill="blue") +
#6
labs(x="海胆(标准化)", y="珊瑚覆盖层")
chin_plot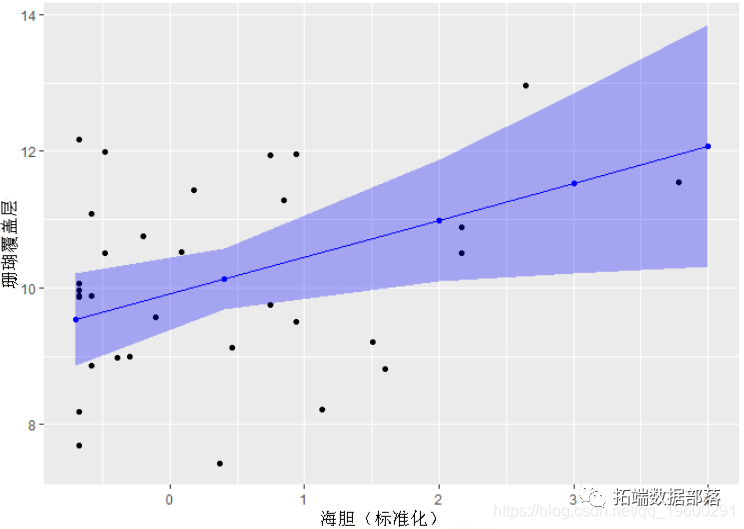

本文摘选《R语言建立和可视化混合效应模型mixed effect model》,点击“阅读原文”获取全文完整资料。

本文中的珊瑚数据分享到会员群,扫描下面二维码即可加群!

点击标题查阅往期内容
R语言 线性混合效应模型实战案例
R语言用潜类别混合效应模型(Latent Class Mixed Model ,LCMM)分析老年痴呆年龄数据
R语言贝叶斯广义线性混合(多层次/水平/嵌套)模型GLMM、逻辑回归分析教育留级影响因素数据
R语言估计多元标记的潜过程混合效应模型(lcmm)分析心理测试的认知过程
R语言因子实验设计nlme拟合非线性混合模型分析有机农业施氮水平
R语言非线性混合效应 NLME模型(固定效应&随机效应)对抗哮喘药物茶碱动力学研究
R语言用线性混合效应(多水平/层次/嵌套)模型分析声调高低与礼貌态度的关系
R语言LME4混合效应模型研究教师的受欢迎程度
R语言nlme、nlmer、lme4用(非)线性混合模型non-linear mixed model分析藻类数据实例
R语言混合线性模型、多层次模型、回归模型分析学生平均成绩GPA和可视化
R语言线性混合效应模型(固定效应&随机效应)和交互可视化3案例
R语言用lme4多层次(混合效应)广义线性模型(GLM),逻辑回归分析教育留级调查数据
R语言 线性混合效应模型实战案例
R语言混合效应逻辑回归(mixed effects logistic)模型分析肺癌数据
R语言如何用潜类别混合效应模型(LCMM)分析抑郁症状
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言建立和可视化混合效应模型mixed effect model
R语言LME4混合效应模型研究教师的受欢迎程度
R语言 线性混合效应模型实战案例
R语言用Rshiny探索lme4广义线性混合模型(GLMM)和线性混合模型(LMM)
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言如何解决线性混合模型中畸形拟合(Singular fit)的问题
基于R语言的lmer混合线性回归模型
R语言用WinBUGS 软件对学术能力测验建立层次(分层)贝叶斯模型
R语言分层线性模型案例
R语言用WinBUGS 软件对学术能力测验(SAT)建立分层模型
使用SAS,Stata,HLM,R,SPSS和Mplus的分层线性模型HLM
R语言用WinBUGS 软件对学术能力测验建立层次(分层)贝叶斯模型
SPSS中的多层(等级)线性模型Multilevel linear models研究整容手术数据
用SPSS估计HLM多层(层次)线性模型模型

![]()