递增的三元子序列
题解部分转自leetcode:Xzz
medium
给你一个整数数组
nums,判断这个数组中是否存在长度为3的递增子序列。如果存在这样的三元组下标
(i, j, k)且满足i < j < k,使得nums[i] < nums[j] < nums[k],返回true;否则,返回false。示例 1:
输入:nums = [1,2,3,4,5] 输出:true 解释:任何 i < j < k 的三元组都满足题意示例 2:
输入:nums = [5,4,3,2,1] 输出:false 解释:不存在满足题意的三元组示例 3:
输入:nums = [2,1,5,0,4,6] 输出:true 解释:三元组 (3, 4, 5) 满足题意,因为 nums[3] == 0 < nums[4] == 4 < nums[5] == 6提示:
1 <= nums.length <= 5 * 105-231 <= nums[i] <= 231 - 1**进阶:**你能实现时间复杂度为
O(n),空间复杂度为O(1)的解决方案吗?
一、题目信息剖析
划重点:给定一个 未排序 的数组,判断这个数组中是否 存在 长度为 3 的 递增 子序列。
所以我们优化算法的根本来源在于抓住 存在 和 长度为3 这个重点进行优化。
题目只需要我们判断存在即可,所以我们只需要找出一个满足题意的条件即可。
要求:O(n)O(n)O(n)的时间复杂度,即遍历一遍数组,要求O(1)O(1)O(1)的空间复杂度,即不使用额外空间。
二、思路详解
核心想法:遍历一遍数组,希望遍历到的这个数three,前面已经有一个比他小的数two,再前面有一个比two小的数one。 我们需要维护两个变量:one和two。代表递增子序列的第一个数和第二个数。 假设我们已经有了这两个数,那么three的大小有以下三种情况:
- three大于two

此情况下:即找到了三元组,直接返回true。
- three介于two和one之间
(three<=two && three>one)

此情况下:应更新two,赋值为这个更小的值。 这相当于帮我们扩大了three的可选择范围,当再次遇到一个比更新过的two大的数即可找到。

- three小于one

此情况下:应更新one,赋值为这个更小的值。而不需要动two。 这相当于帮我们扩大了之后出现的two的可选择范围。进而扩大了之后出现的three的可选择范围。
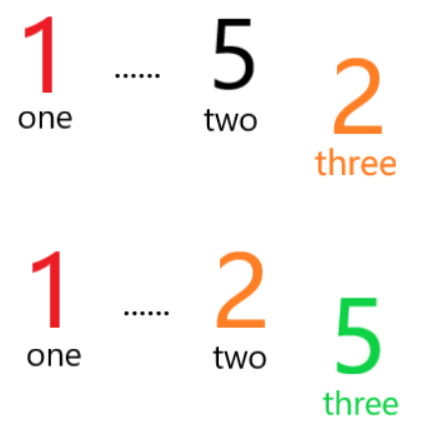
需要注意的是,我们只更新one,原先的two不需要更改,因为子序列是从前往后的,只有当之后再出现比two小的数的时候再按照第二步那样更改。
假设有如下示例:[2,5,1,6],在遇到1之后更新了one,后遇到6,因为先判断是否大于two,由于6大于5,就直接返回true了。

注意:two附带隐含信息——这之前有个数比two小 所以此时找到的递增子序列不是one、two、three的1 5 6,而是old one、two、three的2 5 6。
这里更新的one的意思是,为之后可能存在的更小的递增子序列打基础。 假设有如下示例:[2,5,1,2,6],在遇到1之后更新了one,后遇到2,2介于1和5(two)之间,更新two为2,后遇到6,由于6大于2,返回true。 此时找到的递增子序列才是one、two、three的1 2 6
最后考虑one、two的初值,容易想到设定为Integer.MAX_VALUE (float(“inf”) 正无穷大即可。
三、代码
class Solution:
def increasingTriplet(self, nums: List[int]) -> bool:
one = two = float('inf') # 初始化子序列第一个数和第二个数为正无穷大
for three in nums:#子序列第三个数遍历数组
if three > two:# 第三个数大于第二个数则存在一个递增
return True
elif three <= one:# 第三个数小于等于第一个数,将第三个数赋值给第一个数
one = three
elif three > one and three <= two:# 第三个数大于第一个数并且小于等于第二个数时,将第三个数赋值给第二个数
two = three
return False# 遍历完成没有找到符合的递增序列返回False