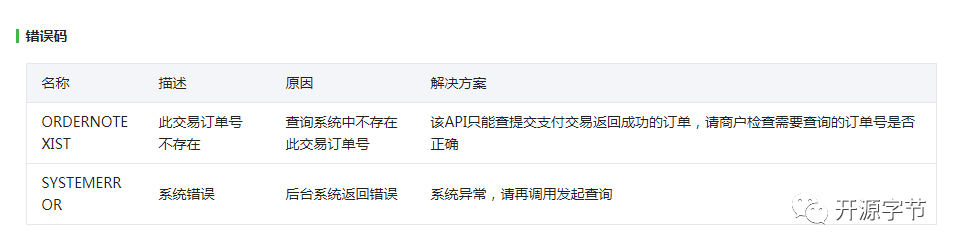
计数排序 (Counting Sort)

计数排序 (Counting Sort)_20230709

news2024/11/25 9:00:27

计数排序(Counting Sort)

前言

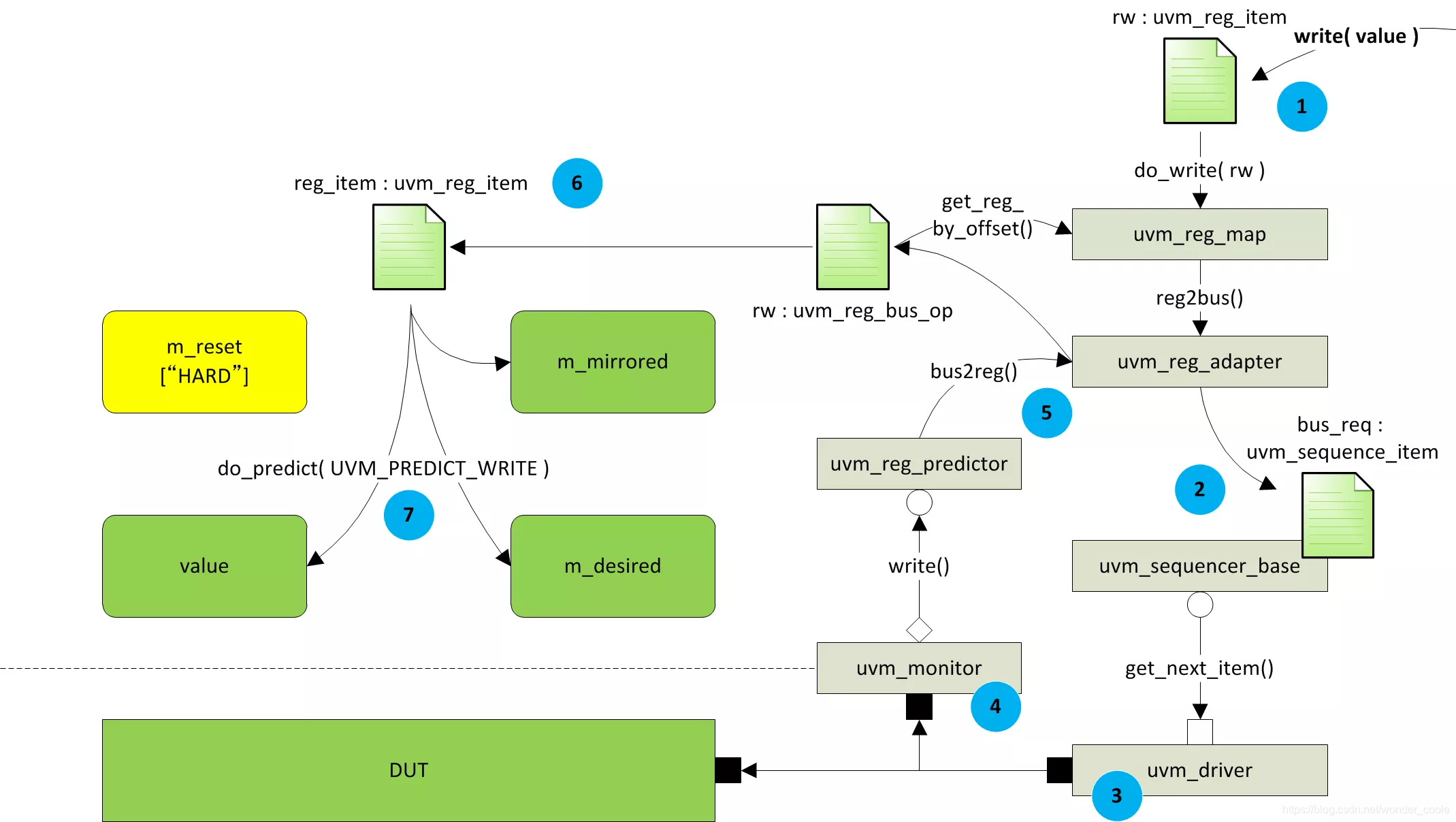
计数排序的对象一般为分布在[0-k]范围内的非负整数，计数器类似哈希函数的线性映射，它确定了数值本身和它在序列中的总数量之间的基本关系。它的本质是计算某个数在临时序列中（原序列大小相同，但下标从1开始）的位置，在后续的映射中，直接把某个位置上放置相关的数值。

计数排序过程

计数排序中至少涉及到三个序列（数组），为了叙述方便，定义待排序数组为A，排序数组为B, 计数数组为C。给定输入数组A[0…n-1]，数组的大小为n，在数组中最大的非负值为k。排序完成的后，数组B[1…n]中的元素为有序序列，值得一提的是，这里B的下标必须从1开始，因为它的下标与计数数组相关，由于A为非空数组，其包含元素数量至少为1。

计数数组的下标为[0…k]，下标的值来自于A[0…n-1]，通过对待排序数组中元素的数量进行统计，从而形成一个计数数组。

形成计数数组后，我们需要对计数的值进行累计处理，也就是需要找到小于它的值数量，也即当前值在B[1…n]数组中所处的位置。给点某个非重复的数字x(distinct)，假定有10个数字小于等于x，那么x在B[1…n]数组中所处的位置为11。

计数排序需要处理序列元素重复的情形，假定序列中包含3个数字x，此时就需要对count[x](累计)进行操作，第一次插入至B[1…n]完成后，count[x]的值就应该自减1，确保第二次排序的时候，所获得count[x]为正确的值，依次直至此处的count[x]自减3为止。

计数排序过程演示

为了更好演示计数排序过程，具体看一个例子。给定待排序的数组A，其中包含8个元素，最大元素的值为5,可以取k值为5或6，也就是计数数组大小设定为6或7。通过对待排序元素进行线性扫描，计算出每个元素的总计数。此时数组C中下标值代表A数组中的元素值[0…k]，数组C中的元素值对应A中等于当前C的下标值的计数值。比如下标为3的C[3]=3代表的含义为原数组中含有3个3。

在这里插入图片描述

对于数组C，目前代表的仅是每个下标值对应的计数数量，要找到其在临时数组B中的插入位置，需要查找每个下标值在B中的位置，那么就需要进行累加求和，也就是计算小于某个下标值（对应A中的值）前面的总的计数和，这样就可以找到在数组B中的插入位置。依照此思路，对数组C进行累加操作，更新C数组值，代表累加值。

在这里插入图片描述

为了保证计数排序的原位(in-place)特性，需要从后向前对数组A中的元素进行遍历，具体看一个例子。首先检查A[7]的值，由于A[7]等于3，然后寻找下标为3的C数组对应的值，C[3]的当前值对应的值就是A[7]应该在数组B中应该放置的位置，也即B[7]=3。考虑到A中的存在重复元素的可能性，所以当[7]位置放置3后，需要对C[3]自减1，以便正确放置后续重复元素，具体过程对应为：

在这里插入图片描述

为了更加深入理解过程，再对A[6]进行相关操作演示。通过观察A[6]对应的值为0，而C[0]的值对应A[6]值放置的位置，所以B[2]=A[6]，同上分析，对C[0]当前的值进行自减，C[0]由2减少至1。

在这里插入图片描述

通过不断的向前遍历，最终我们得到B数组的值为，

在这里插入图片描述

细心的读者可能以及发现，B数组对应的下标从1开始，它包含的元素数量和A数组相同，也即n下标结束。

代码实现

取决于数据对象的不同，计数排序可归为两种方式，第一类方式假定数据对象不仅包含键值，而且每个键值伴随着其它不同的相关信息值；第二类方式假定操作对象仅为非负整数，这个过程可以省略数组B，从而使操作过程所占空间优化。

4.1 第一类方式

头函数counting_sort.h

/**
 * @file counting_sort.h
 * @author your name (you@domain.com)
 * @brief 
 * @version 0.1
 * @date 2023-06-29
 * 
 * @copyright Copyright (c) 2023
 * 
 */
#ifndef COUNTING_SORT_H
#define COUNTING_SORT_H
#include <stdlib.h>
#include <string.h>
#include <stdio.h>

/**
 * @brief Find the k value that makes sure value in arr array falls into [0...k]
 * 
 * @param arr Array 
 * @param n  Number of element in the array
 * @return int -Return k value
 */
int  find_k_value(int *arr, int n);

/**
 * @brief Use addtional array temp[] to realize the counting sort function
 * 
 * @param arr Array object
 * @param n Number of element in the array
 */
void counting_sort(int *arr,int n);

/**
 * @brief Display the element in the array
 * 
 * @param arr Array object
 * @param n Number of element in the array
 */
void display_list(int *arr, int n);

#endif

函数实现

/**
 * @file counting_sort.c
 * @author your name (you@domain.com)
 * @brief 
 * @version 0.1
 * @date 2023-06-29
 * 
 * @copyright Copyright (c) 2023
 * 
 */
#ifndef COUNTING_SORT_C
#define COUNTING_SORT_C
#include "counting_sort.h"

void counting_sort(int *arr, int n)
{
   // Use count[K] to keep record of the number of element
   int k;
   int i;
   int j;
   k = find_k_value(arr, n);
   int count[k];
   int temp[n+1];

   memset(count,0,sizeof(int)*k);

   for(i=0;i<n;i++) //start from the index 0;
   {
        count[arr[i]]++;
   }

   for(j=1;j<k;j++) //start from j=1 instead of j=0
   {
        count[j]=count[j]+count[j-1];
   }

   for(i=n-1;i>=0;i--)
   {
        temp[count[arr[i]]]=arr[i];
        count[arr[i]]--;
   }

   memcpy(arr,temp+1,sizeof(int)*n);

   return;

}

int find_k_value(int *arr, int n)
{
    int max_value=-1;
    int i;

    for(i=0;i<n;i++)
    {
        if(max_value< arr[i])
        {
            max_value=arr[i];
        }
    }

    return max_value+1;
}

void display_list(int *arr, int n)
{
    int i;

    for(i=0;i<n;i++)
    {
        printf("%d ",arr[i]);
    }
    
    printf("\n");
}

#endif

测试函数

/**
 * @file counting_sort_main.c
 * @author your name (you@domain.com)
 * @brief 
 * @version 0.1
 * @date 2023-06-17
 * 
 * @copyright Copyright (c) 2023
 * 
 */
#ifndef COUNTING_SORT_MAIN_C
#define COUNTING_SORT_MAIN_C
#include "counting_sort.c"

int main(void)
{
    int arr[] = {2, 8, 3, 0, 2, 3, 8, 3};
    int n = sizeof(arr) / sizeof(int);

    printf("The number is listed before sorting:\n");
    display_list(arr, n);

    counting_sort(arr,n);

    printf("The number is listed after sorting:\n");
    display_list(arr, n);

    getchar();

    return EXIT_SUCCESS;
}


#endif

4.2 第二类方式

为了方便读者阅读，仅对主函数进行展现，

void counting_sort(int *arr, int n)
{
    int         i;
    int         j;
    int         k;
    int         m = find_k_value(arr, n);
    int         count[m];

    memset(count,0,sizeof(int)*m);

    for(i=0;i<n;i++)
    {
        count[arr[i]]++;
    }

    for(j=0,k=0;j<m;j++)
    {
        while(count[j]) //lean code
        {
            arr[k]=j;
            k++;
            count[j]--;
        }
    }
}