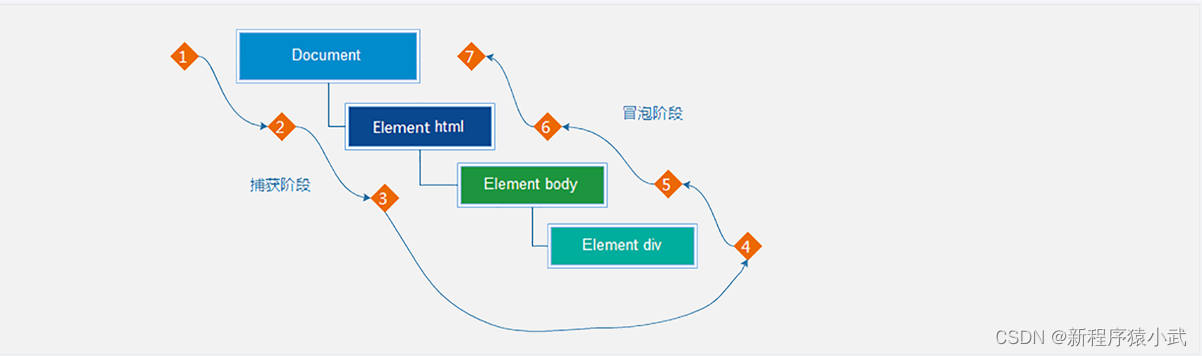
目录
题述:
思路:
正确代码如下:
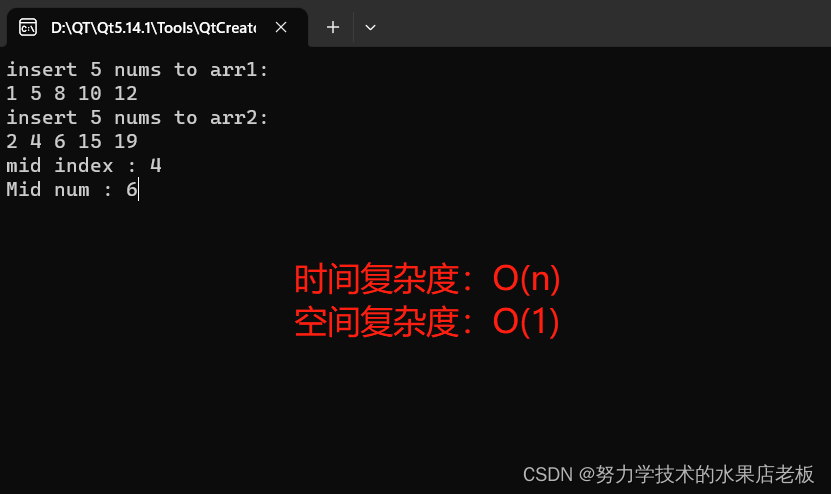
时间复杂度分析:
现让你把代码优化时间复杂度为O(N)
思路:
题述:
给定一个二叉树,判断他是否是高度平衡的二叉树。
本题中,一颗高度平衡二叉树的定义为:
一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1
示例1:
输入:root = 【3,9,20,NULL,NULL,15,7】
输出:true
题中已给:
struct TreeNode
{
int val;
struct TreeNode* left;
struct TreeNode* right;
};
bool isBalanced(struct TreeNode* root)
思路:
利用之前讲过的求树的深度的函数TreeDepth来求解这道题,根,左子树,右子树不断往下遍历,左子树又分为根,左子树,右子树,右子树又分为根,左子树,右子树直到遇到空树,对于每一个树都求一下左右子树的深度,然后判断一下树的高度是否>1,>1则不满足,<1则继续递归遍历,直到整棵树判断完毕,才可确定是平衡二叉树。整体思路类似于根左右,即先判断当前树,再判断左子树,再判断右子树
正确代码如下:
int TreeDepth(struct TreeNode* root)
{
if (root == NULL)
{
return 0;
}
int leftDepth = TreeDepth(root->left);
int rightDepth = TreeDepth(root->right);
return leftDepth > rightDepth ? leftDepth + 1
: rightDepth + 1;
}
bool isBalanced(struct TreeNode* root)
{
//空树满足平衡二叉树的定义
if (root == NULL)
{
return true;
}
//先判断当前树是否满足
int gap = TreeDepth(root->left) - TreeDepth(root->right);
gap = abs(gap);//取绝对值
if (gap > 1)
{
return false;
}
//再判断左右子树是否满足
return isBalanced(root->left)
&& isBalanced(root->right);
}时间复杂度分析:
假设该二叉树有N个结点。
TreeDepth函数是把整个二叉树遍历了一遍,故时间复杂度:O(N)
对于isBalanced函数,它的遍历是根左右,下面给个二叉树方便说明这个问题
①、先会判断当前树(以3为根节点的树)左右深度的差的绝对值,这一次就遍历了一遍树,次数为N
②、再判断左子树(以9为根节点的树)左右深度的差的绝对值,也就是以9为根节点的左右子树的高度要再求一遍,为什么是“再”?求以3为根节点的左子树的深度时,已经算过以9为根结点的树的深度了,所以先序遍历存在重复的深度计算。
那这种方法的时间复杂度:以3为根节点为N次,以其它节点为根节点均为N-常数次,总的时间复杂度加起来大概可以构成等差数列(N+N-常数+N-常数...),由等差数列前n项和公式:
N(N+N-常数) / 2 = O(N*N)
现让你把代码优化时间复杂度为O(N)
思路:
上面的代码时间复杂度慢在树的深度的重复计算,我们只要让树的深度算一遍就可以使时间复杂度优化到O(N)了,怎么做到深度只算一遍?即利用后序遍历:左右根,先判断左子树再判断右子树最后再判断当前树。我们不调用TreeDepth函数,而是每次在判断是否是平衡二叉树的同时,返回当前树的深度给上层(递归往回返的过程)。那就意味着深度和是否为平衡二叉树(返回真假)每次都要返回,法一:考虑返回结构体,结构体包含这两个。法二:参数传深度的地址,每次调用在需要改的时候改,函数返回真假。
bool isBalanced(struct TreeNode* root, int * depth)
{
//如果为空树
if (root == NULL)
{
*depth = 0;
return true;
}
//先判断左子树
int leftdepth = 0;
if (isBalanced(root->left, &leftdepth) == false)
return false;
int rightdepth = 0;
if (isBalanced(root->right, &rightdepth) == false)
return false;
//再判断当前树,当前树是否满足平衡二叉树,看左右子树高度差的绝对值是否>1
if (abs(leftdepth - rightdepth) > 1)
return false;
//左右子树,当前树都满足平衡二叉树的前提下
*depth = leftdepth > rightdepth ? leftdepth + 1
: rightdepth + 1;
return true;
} 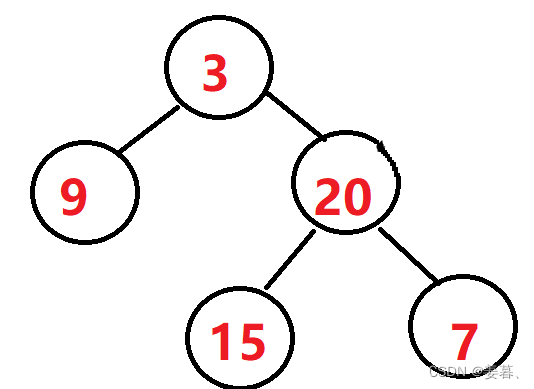
以此二叉树为例,上述代码的执行过程如下:
①、root=3时,判断左子树,转为root=9,判断左子树,左子树为NULL,故9的左子树深度为0,return true,同理9的右子树深度为0,return true。再判断以9为根节点的当前树,深度差不>1,故高度为0+1=1,return true,至此算出以9为根节点的深度为1,并判断为满足平衡二叉树。
②、再判断root=3时的右子树,转为root=20,判断左子树,转为root=15,判断它的左子树, 为NULL,故15的左子树深度为0,return true,同理,15的右子树的深度为0,return true。再判断以15为根节点的当前树,深度差不>1,故高度为0+1=1,return true,至此算出以15为根节点的深度为1,并判断为满足平衡二叉树。
③、再判断20的右子树,同理上面,以7为根节点的深度为1,并判断为满足平衡二叉树。至此,20的左右子树判断完毕,再判断以20为根节点的当前树,深度差不>1,故深度为1+1=2,return true,至此算出以20为根节点的深度为2,并判断为满足平衡二叉树。
④、至此3的左右子树判断完毕,再判断以3为根节点的当前树,深度差不>1,故深度为2+1=3,return true,至此算出以3为根节点的深度为3,并判断整棵树满足平衡二叉树。