代码随想录第24天 | ● 93.复原IP地址 ● 78.子集 ● 90.子集II

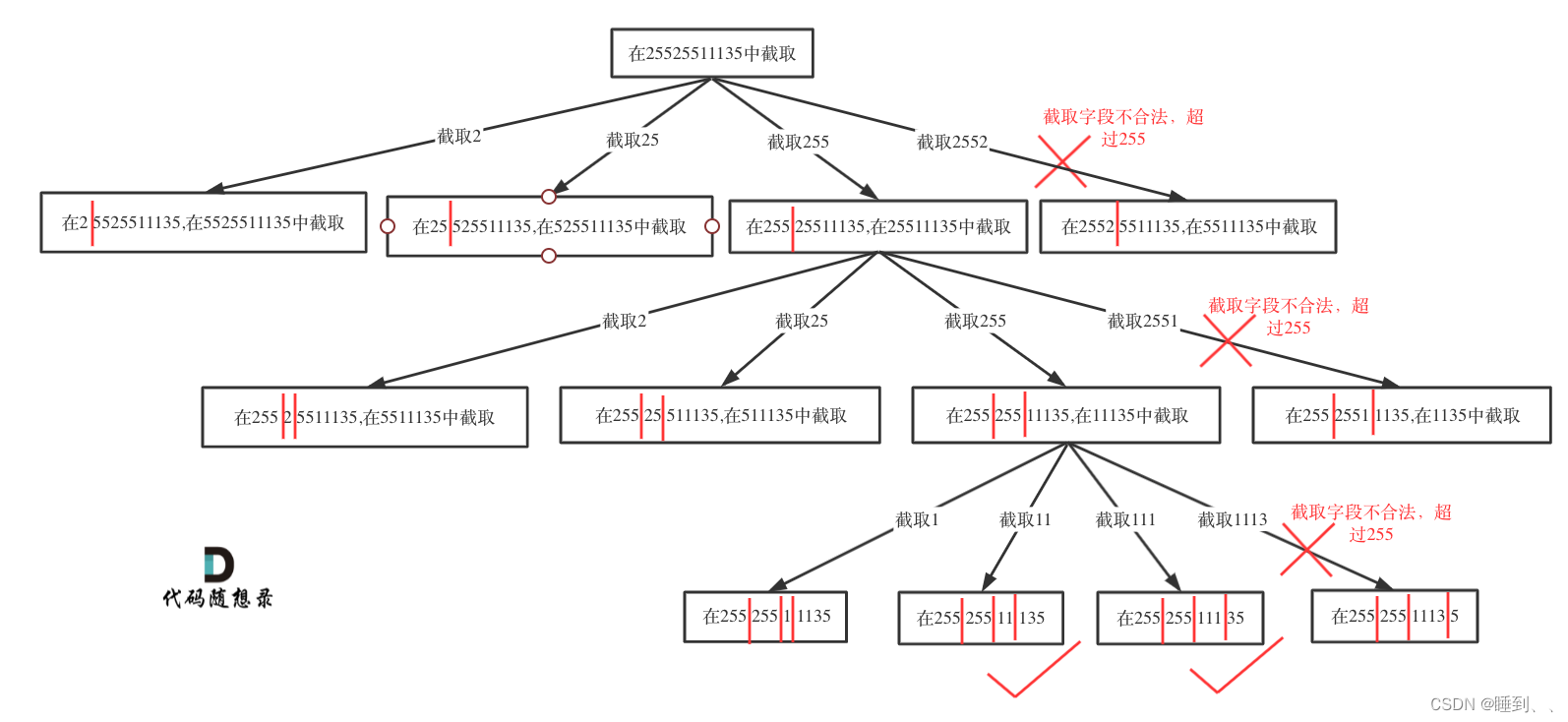
93.复原IP地址

      /**
       * @param {string} s
       * @return {string[]}
       */ let road = [];
      let path = [];
      var restoreIpAddresses = function (s) {
        road = [];
        if (s.length > 12 || s.length < 4) return [];//开始就判断，长度大于12的字符窜或者小于4的都不行
        backtracking(s, 0);
        return road;
      };

      let backtracking = function (s, er) {
        if (er === s.length) { //结束条件
          if (path.length === 4) road.push(path.join(".")); //只能4个
          return;
        }
        for (let i = er; i < s.length && i < er + 3; i++) {  //i只能加三位数
          if (path.length === 1 && (s.length - er > 9 || s.length - er < 3))   //分割了一个，剩下的3个分
            continue;
          if (path.length === 2 && s.length - er > 6) continue;
          if (path.length === 3 && s.length - er > 3) continue;
          if (ip(s, er, i)) {
            let ss = s.slice(er, i + 1);
            path.push(ss);
          } else continue;
          backtracking(s, i + 1);
          path.pop();
        }
      };
      let ip = function (s, start, end) {//判断是否满足
        if (s[start] === "0" && start !== end) return false;
        let num = Number(s.slice(start, end + 1));
        if (num > 255) return false;
        return true;
      };

思想

在这里插入图片描述

困难

注意条件，和剪枝，可以加一些条件减少时间空间复杂度
然后其实有个条件，必须是数字，但是我在 let num = Number(s.slice(start, end + 1));
if (num > 255) return false;这步做了

78.子集

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
  let road = [];
  let path = [];
  
var subsets = function(nums) {
  road = [[]]  //road会有之前的数据，所以需要每次清空road
  brektraning(nums, 0);
  return road;
};
  const brektraning = function (nums, er) {
    // if (er===nums.length) {  //收割
    //   return;
    // }
    for (let i = er; i < nums.length; i++) { 
      path.push(nums[i]);
      brektraning(nums, i + 1);
      road.push([...path]);  //push不能为数组，所以只能先展开
      path.pop();
    }
  };

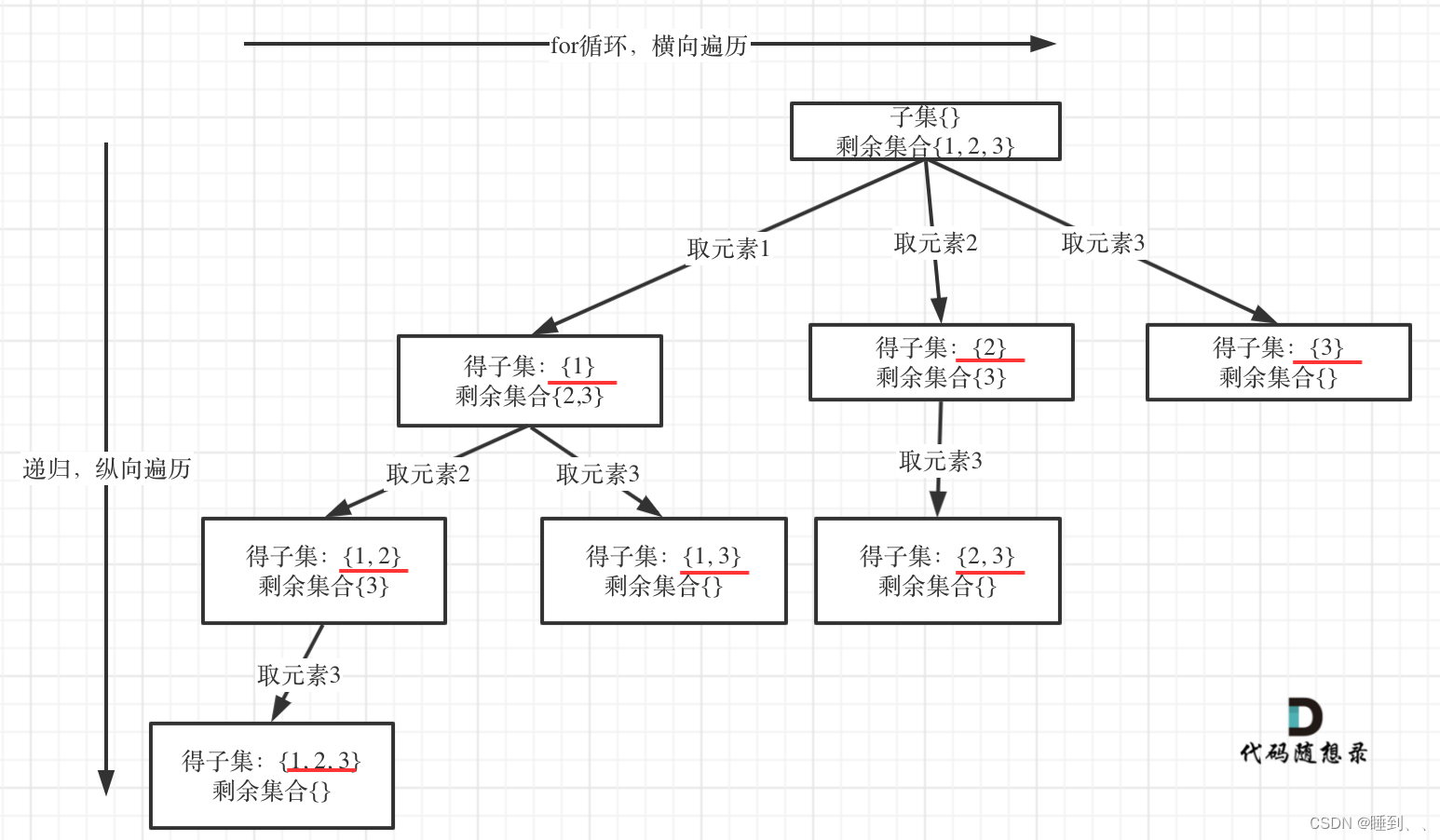
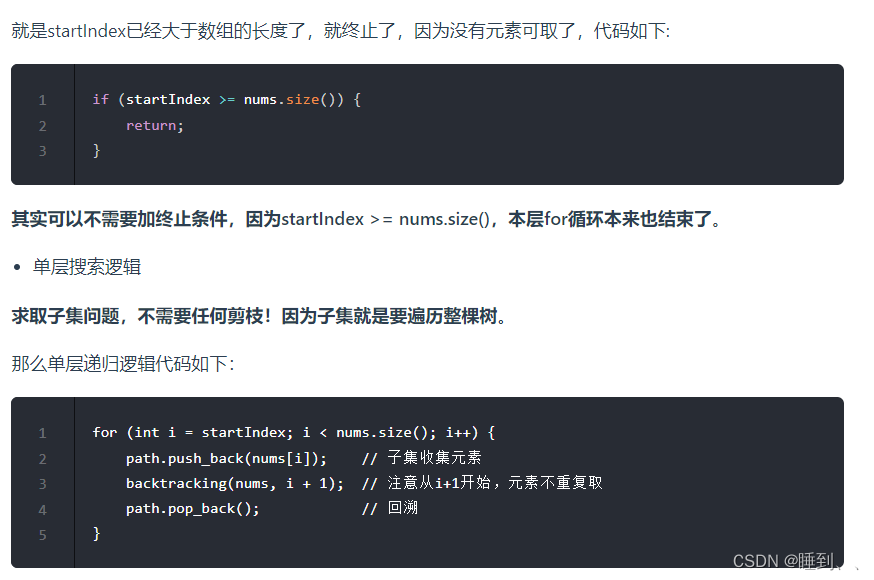
想法

在这里插入图片描述

困难

收获

子集是收集树形结构中树的所有节点的结果，而组合问题、分割问题是收集树形结构中叶子节点的结果。

90.子集II

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
  let road = [];
  let path = [];
  
var subsetsWithDup = function(nums) {
  road = [[]]  //road会有之前的数据，所以需要每次清空road
   nums.sort((a, b) => a - b); // 排序
  brektraning(nums, 0);
  return road;
};
  const brektraning = function (nums, er) {
    // if (er===nums.length) {  //收割
    //   return;
    // }
    for (let i = er; i < nums.length; i++) { //剪枝
      path.push(nums[i]);
      brektraning(nums, i + 1);
      road.push([...path]);  //push不能为数组，所以只能先展开
      path.pop();
        while (nums[i + 1] && nums[i] === nums[i + 1]) i++; //去重
    }
  };