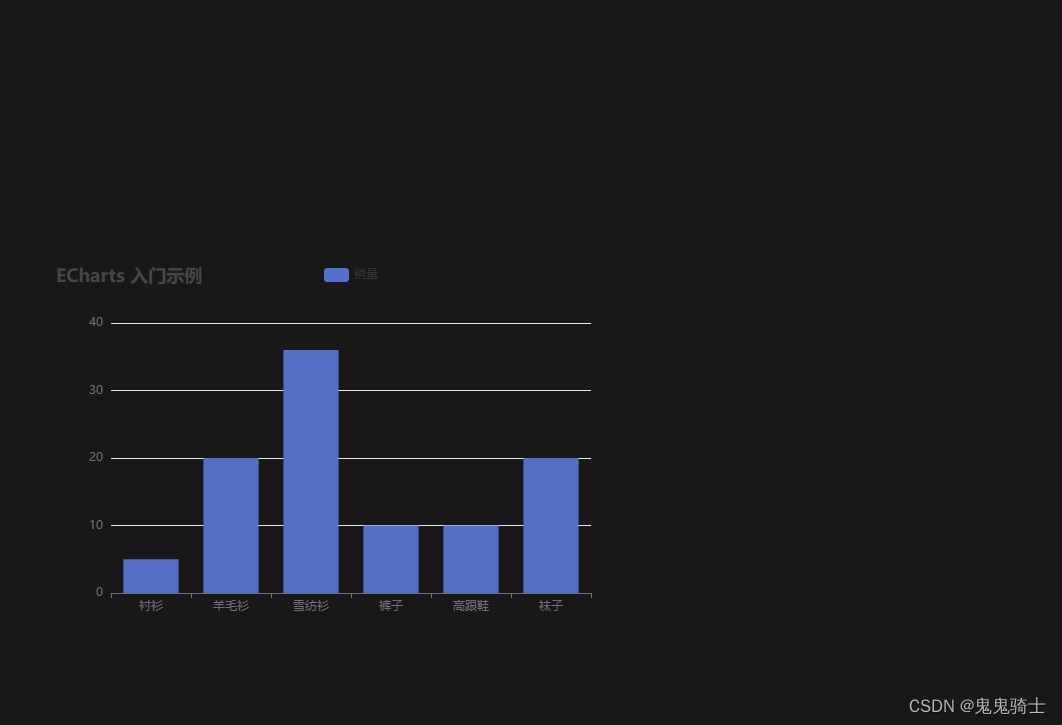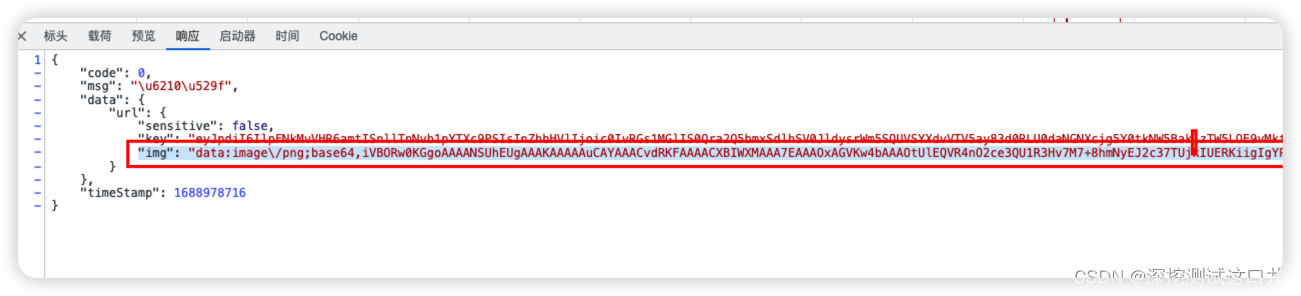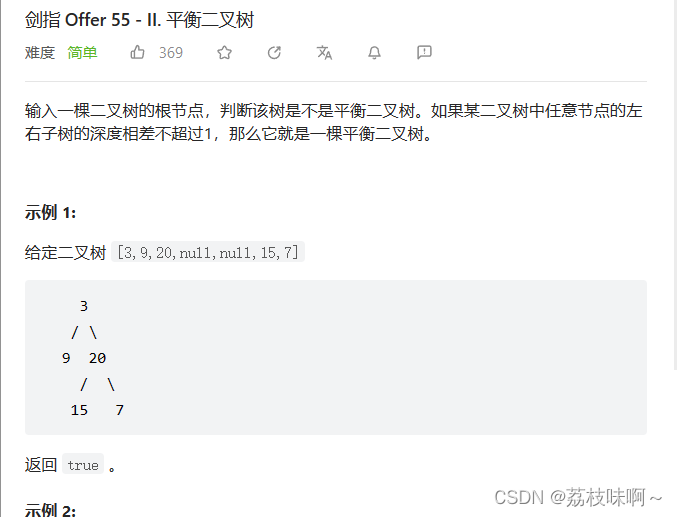
我这个方法比较笨，用的是用的是昨天写的求二叉树深度的方法，先定义dfs求二叉树深度的方法，再定义cur方法，比较左子树和右子树的深度，递归比较每一个子树的左子树和右子树的深度，一旦有一个不平衡就把flag改为false，最后返回flag。

class Solution {
    int height =0;
    boolean flag =true;
    public boolean isBalanced(TreeNode root) {
        if(root == null)return true;
        cur(root);
        return flag; 
    }
    private int dfs(TreeNode root){
        if(root == null) return 0;
        int lHeight = dfs(root.left);
        int rHeight = dfs(root.right);
        return  Math.max(lHeight, rHeight) + 1;
    }
    private void cur(TreeNode root){
        int leftHeight, rightHeight =0;
        if(root.left != null){
            leftHeight = dfs(root.left);
        }else{
            leftHeight = 0;
        }
        if(root.right != null){
            rightHeight = dfs(root.right);
        }else{
            rightHeight = 0;
        }
        if(rightHeight - leftHeight > 1 || leftHeight - rightHeight > 1){
            flag = false;
        }
        if(root.left != null)cur(root.left);
        if(root.right != null)cur(root.right);

    }

}

写完后我看了一下题解，题解也是用了两次递归，但是他的代码很简洁

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        } else {
            return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
        }
    }

    public int height(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            return Math.max(height(root.left), height(root.right)) + 1;
        }
    }
}

第一次递归和我的差不多，主要是第二次递归简单，如果一棵树要做到是平衡的，那么左右子树的高度相差必须小于等于1，并且左子树是平衡的右子树也是平衡的。

题解还给了一种自底向上的方法，这个也好理解。

class Solution {
    public boolean isBalanced(TreeNode root) {
        return height(root) >= 0;
    }

    public int height(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = height(root.left);
        int rightHeight = height(root.right);
        if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {
            return -1;
        } else {
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}

这个方法和前面那个方法的求高度方法差不多，唯一改变的就是，如果一颗树的左子树和右子树的高度之差大于1或者他的左子树或右子树的高度是-1，那么这棵树的高度就是-1.这就会导致如果出现了左右子树相差大于1，那么这棵树和他的所有祖宗树的高度都是-1，也就是说最大的根树也是-1，主方法中调用这个方法直接返回树的高度是否大于等于0，如果是-1就是false，其他都是true。