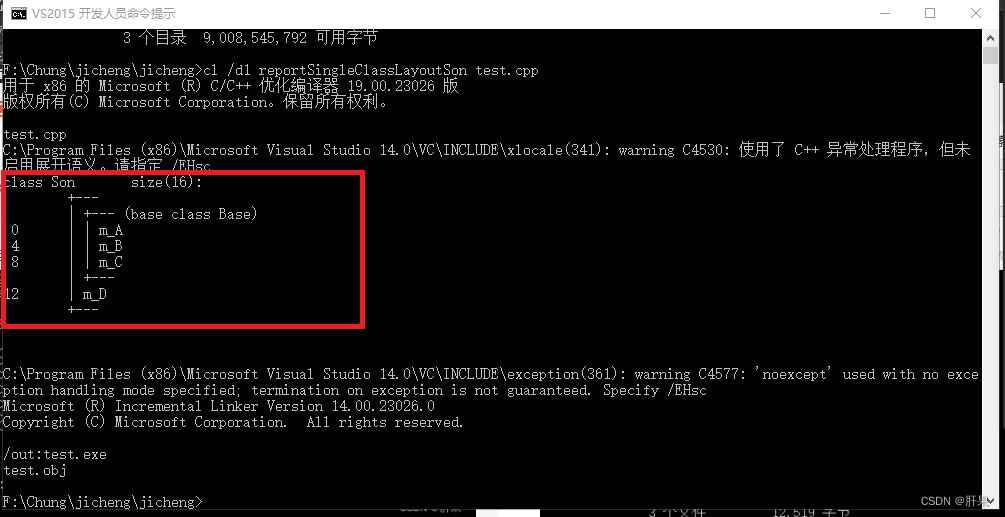
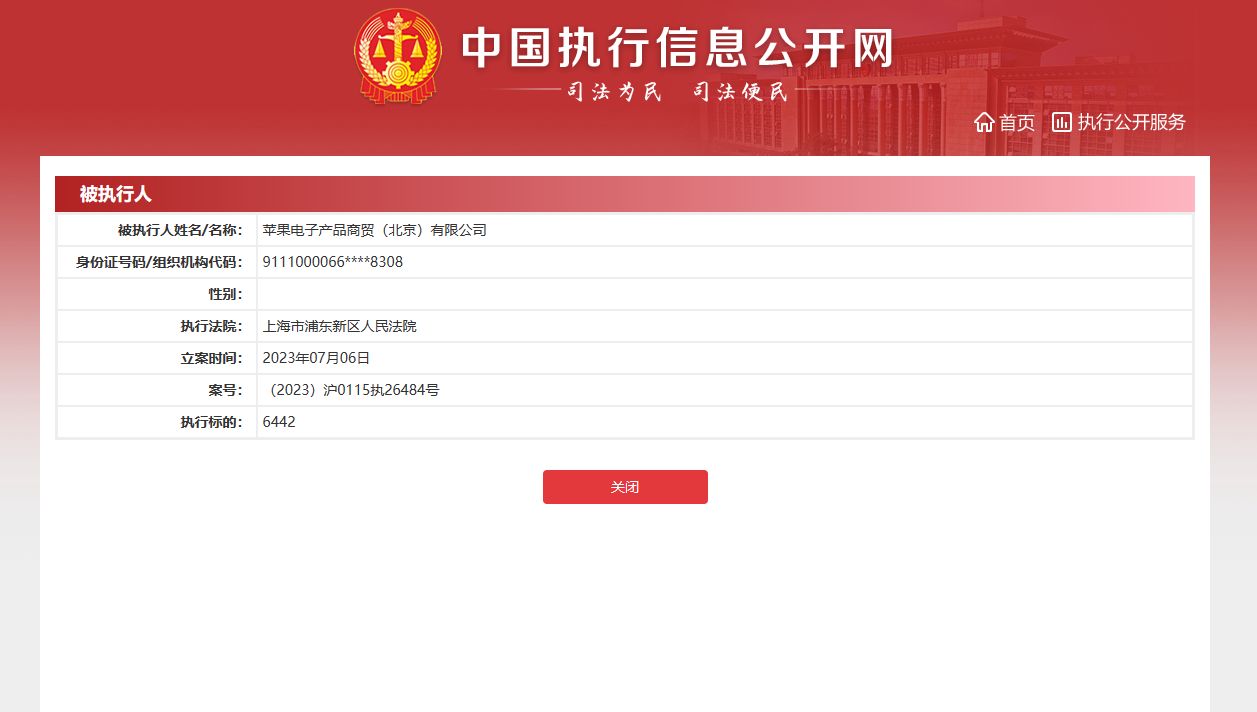
根据中国执行信息公开网等消息，苹果电子产品商贸（北京）有限公司最近在买卖合同纠纷方面被执行，执行金额为6442元，案件由上海市浦东新区人民法院审理，目前尚未获取到详细纠纷信息。

近日，苹果公司在中国市场又遇到了麻烦。据相关媒体报道，苹果电子产品商贸（北京）有限公司因违反广告法被北京市东城区市场监督管理局罚款3万元，公示日期为2023年7月5日。

根据北京市东城区市场监督管理局的调查结果，苹果公司的"iPhone 年年焕新计划"主页广告中包含了“升级至最新款iPhone，轻松畅享”的字样以及“欲加入iPhone 年年焕新计划，只需一次购买指定新款iPhone并同时加购AppleCare+服务计划即可参与计划”的说明。然而，在实际执行中，该计划无法与商务折扣同时享受。