最近,我不得不想出一种方法,从三次 Hermite 样条曲线创建平行曲线,例如铁路车道。 首先,我只是沿着法线方向移动它们的开始/结束控制点,同时保持相同的开始/结束切线。 它在大多数情况下工作得很好,因为我的用例中的大多数样条曲线都不是很弯曲。

推荐:用 NSDT设计器 快速搭建可编程3D场景。
但我很快发现,即使使用一些轻微弯曲的样条线,以这种天真的方式复制的曲线也常常会导致变窄。 因此,我决定硬着头皮通过谷歌搜索来了解其他聪明人已经弄清楚的内容。

我很快了解到这种曲线的官方术语是偏移曲线(offset curve)或平行曲线(parallel curve)。 我遇到的第一种方法是将曲线转换为折线,偏移折线,然后将其重建为一条或多条曲线。这听起来很复杂,我想找到一种更直接的方法,不需要经历折线阶段。
我发现的下一个方法是偏移其控制多边形(这里 和 这里)。 你可以轻松地将三次 Hermite 样条曲线转换为 Bézier 曲线,如 这里所解释的。 在贝塞尔曲线形式中,你可以从四个控制点获得一个控制多边形。 可以按如下方式偏移它并从中获取偏移样条线:
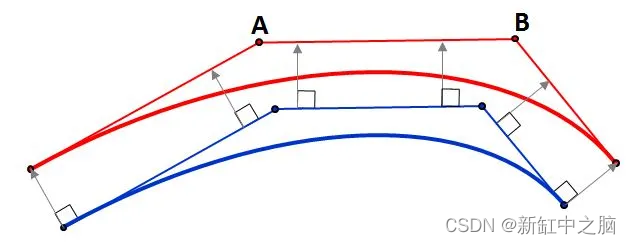
正如上面的两个链接所提到的,该方法不适用于高曲率的曲线,你需要将原始曲线分割为多个段才能在这种情况下获得更好的结果。 我认为拆分/细分对于我的用例来说不是必要的,因此决定尝试该方法。
我有 3D 样条线,因此我使用倾斜线之间的距离方程(如这里)来获取控制多边形的偏移边缘之间的交点。 我的样条线对于每个控制点也只有一条切线。 换句话说,没有单独的传入/传出切线。 因此,一旦计算了相邻线段的偏移样条线,我就会将共享控制点的切线设置为第一个线段的结束切线和第二个线段的开始切线的平均值。
该方法提供的平行曲线对于我拥有的大多数样条线来说看起来足够好。 但是,当切线很长且控制多边形自相交时,某些偏移曲线会变得很糟糕。 此外,对于其他一些情况,它们有点过度补偿并且变得比应有的范围更宽。
因此,我引入了一些调整,例如当控制多边形的内角太锐时回到朴素方式,并在朴素结果和基于内角余弦的方法之间进行调整,以避免在某些情况下变得太宽 。 在极少数情况下,这种调整后的方法仍然会失败。 对于他们来说,我可以在这种方法之前应用分割,但是现在,我决定手动修改原始样条线,以便它们可以在没有自动分割的情况下更好地使用该方法。 我认为每个控制点有一个切线(没有单独的传入/传出切线)也会使其中一些情况变得更糟。
如你所见,这并不完全令人满意。 它需要一些不太干净的调整,但仍然无法处理所有情况。 我在业余时间挖掘了更多内容,发现了一些有用的信息和更多值得将来尝试的方法。 此存档的 PDF 文档解释了通过求解三个线性方程组获得贝塞尔偏移曲线, 从第 34 页开始。它从简单的方法开始,通过求解具有三个未知数的线性方程组来计算应如何修改所得曲线以满足理想偏移曲线的属性。 该方法也有一些失败案例,该文档解释了一种通过修复一个未知数并仅使用两个线性方程来处理这些失败案例的方法。 它在 Postscript 中有示例代码。
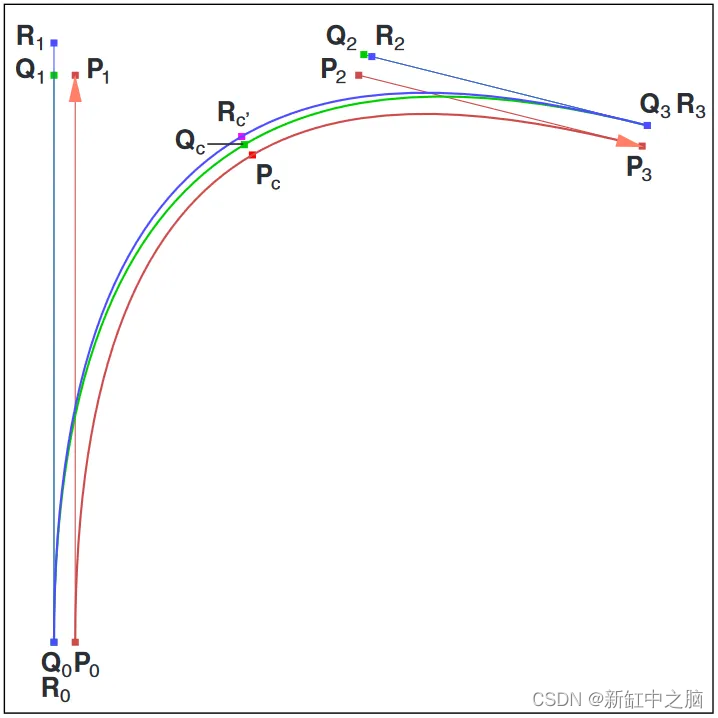
许多参考资料告诉你,一般来说,无法使用另一条贝塞尔曲线(或任何多项式参数曲线,就这一点而言,无论你愿意采用何种高阶)来表达贝塞尔曲线的偏移曲线。 这里第28页还说任意三次曲线的偏移曲线需要10阶代数曲线。
github上有一本关于贝塞尔曲线的非常漂亮且详细的入门书,其中包含有关贝塞尔曲线的各种有用信息,以及交互式和视觉指南。 它的偏移曲线部分解释了另一种涉及分割的方法。 有了它,你可以“将一条曲线切成‘安全’子曲线(其中安全意味着所有控制点始终位于基线的一侧,并且 t=0.5 处的曲线中点大致位于中心) 由曲线坐标定义的多边形),然后相对于其缩放原点(即起点和终点处的点法线的交点)对每个子曲线进行点缩放。” 它在这个仓库中有所有相关代码,因此你可以轻松查看其实现细节。
上面提到的两种替代方案听起来很合理,而且看起来实施起来并不难。 当当前偏移控制多边形的方法对于我的用例来说变得过于脆弱和麻烦时,我将尝试它们。
我的这个简短的研究对我来说是一次非常有趣和有教育意义的旅程,它展示了如何获得样条曲线的并行版本这一看似简单的问题所涉及的细微差别和复杂性。 我希望它对你来说很有趣并且有帮助!
原文链接:三次样条的偏移曲线计算 — BimAnt