描述

众所周知，Fibonacci数列是一个著名数列。它的定义是：

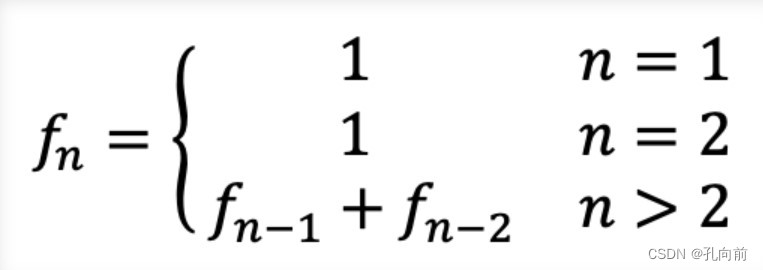
本组题目共有 5 题，请分别用 5 种不同的方式来完成，并比较这些做法的时间。
本题要求采用第一种方法：递归，且不得使用数组记忆结果。

输入描述

每行一个整数 i ，表示 Fibonacci 数列的第 i 项。i ≤ 46
如果你不知道本题规定做法的时间复杂度，计算一下 2 的 46 次幂有多大，就知道了。

输出描述

对每个输入的整数 i，输出一行结果：Fibonacci 数列的第 i 项对 100000009 取模的结果。

注意

本题要求模运算的目的是防止运算结果上溢出：在循环中的每一次加法，均执行求模，即可防止溢出。
加法模运算规则：
( a + b ) % c = ( ( a % c ) + ( b % c ) ) % c
请用递归方法求解本题，否则判 cheat 且 封号 。 不会写递归函数的，请先看书学会再写。

一道简单的oj题，主要是对递归的简单使用，话不多说，上代码

#include<stdio.h>
int fio(int n);
int main(){
	int aa;
	while(scanf("%d",&aa)!=EOF&&aa<=46){
		printf("%d\n",fio(aa));
	}
} 
int fio(int n){
	if(n==1)
		return 1;
	else if(n==0)
		return 0;
	else
		return (fio(n-1)+fio(n-2))%100000009;
}