重建二叉树

描述

给定节点数为 n 的二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。

例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示。

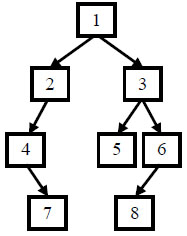
提示:

1.vin.length == pre.length

2.pre 和 vin 均无重复元素

3.vin出现的元素均出现在 pre里

4.只需要返回根结点，系统会自动输出整颗树做答案对比

数据范围： $n \leq 2000$ ，节点的值 $- 10000 \leq v a l \leq 10000$

要求：空间复杂度 $O (n)$ ，时间复杂度 $O (n)$

示例1

输入：

[1,2,4,7,3,5,6,8],[4,7,2,1,5,3,8,6]

返回值：

{1,2,3,4,#,5,6,#,7,#,#,8}

说明：

返回根节点，系统会输出整颗二叉树对比结果，重建结果如题面图示

示例2

输入：

[1],[1]

返回值：

{1}

示例3

输入：

[1,2,3,4,5,6,7],[3,2,4,1,6,5,7]

返回值：

{1,2,5,3,4,6,7}

思路

说实话我对数据结构这部分比较差，所以看了一些别人解法，大部分都是使用的递归。正好递归又是我最不熟悉的一种算法，所以正好借这题来复习一下数据结构和递归算法。

首先看题目的意思是给出一个二叉树的前序遍历和中序遍历，要求给出二叉树。

比如题目输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}

那么构造出来的二叉树就是

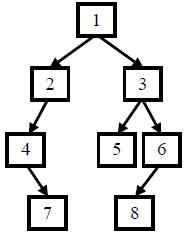
然后输出就是从根节点开始从左到右依次输出，所以输出结果为{1,2,3,4,5,6,7,8}

接着分析一下如何使用递归方法构造二叉树：

首先对于前序遍历，第一个元素肯定是根节点，接着再从中序遍历中找到根节点的位置，其左边则为左子树，右边即为右子树。然后对于前序遍历的左子树的第一个元素又是左子树的根节点，同理右子树。所以就可以根据此递归下去。

比如题目给的两个序列：

preOrder={1,2,4,7,3,5,6,8}
vinOrder={4,7,2,1,5,3,8,6}

那么根节点就是1，然后再根据1将中序遍历分为两半，即{4,7,2}为左子树，{5,3,8,6}为右子树，然后根据前序遍历的{2,4,7}可得左子树的根节点是2，所以左子树的左子树为{7,2}，然后以此类推

所以具体的实现步骤为：

每次递归都取出前序遍历序列的第一个元素作为根节点
根据根节点将中序遍历序列分为左子树和右子树两个序列
对左右子树分别进行同样的递归，直到序列为空

代码实现：

if (preOrder.length == 0 || vinOrder.length == 0) {//子树为空则结束递归
    return null;
}
TreeNode root = new TreeNode(preOrder[0]);		//根节点为前序序列第一位
for (int i = 0; i < vinOrder.length; i++) {		//遍历中序序列
    if (root.val == vinOrder[i]) {				//找到根节点位置
        //递归左子树
        root.left = reConstructBinaryTree(Arrays.copyOfRange(preOrder, 1, i + 1),Arrays.copyOfRange(vinOrder, 0, i));
        //递归右子树
        root.right = reConstructBinaryTree(Arrays.copyOfRange(preOrder, i + 1, preOrder.length), Arrays.copyOfRange(vinOrder, i + 1, vinOrder.length));
        break;
    }
}
return root;

完整代码

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param preOrder int整型一维数组
     * @param vinOrder int整型一维数组
     * @return TreeNode类
     */
    public TreeNode reConstructBinaryTree (int[] preOrder, int[] vinOrder) {
        // write code here
        if (preOrder.length == 0 || vinOrder.length == 0) {
            return null;
        }
        TreeNode root = new TreeNode(preOrder[0]);
        for (int i = 0; i < vinOrder.length; i++) {
            if (root.val == vinOrder[i]) {
                root.left = reConstructBinaryTree(Arrays.copyOfRange(preOrder, 1, i + 1),
                                                  Arrays.copyOfRange(vinOrder, 0, i));
                root.right = reConstructBinaryTree(Arrays.copyOfRange(preOrder, i + 1,
                                                   preOrder.length), Arrays.copyOfRange(vinOrder, i + 1, vinOrder.length));
                break;
            }
        }
        return root;
    }
}